RL电路的零输入响应特性

图4.10所示是一个RL电路,该电路由直流电流源i 0,电阻R 0和R,电感L和开关k组成。t=0时刻前,开关k一直处于闭合状态。t=0时刻,开关打开。下面分析t＞0之后的电感电流i L(t)。

图4.10　RL电路零输入响应

当t＜0时,开关闭合,电路为电流源并联电阻R 0、R和电感L。当电源为直流电流源时,电感可视为短路。经过一段时间后,流过电感的电流等于直流电流源电流,且电路达到稳定状态。

用t=0-来表示开关打开前的瞬间,用t=0+表示开关打开后的初始瞬间。由于电感电流的连续性,不会发生跳变。因此,电感电流在开关打开瞬间是不变的,开关打开后电感电流的初始值为

当t＞0时,开关k打开,电路为电阻R和电感L串联。根据KVL方程,可知

根据电感VCR

由式(4.28)和式(4.29)可得一个一阶齐次微分方程

结合式(4.27)所示电感电流的初始值,该方程的解为(https://www.xing528.com)

其中,I 0为电感电流换路之后的初始值。此外,电感电流的变化还与值的大小有关。

值得注意的是,电感电流的表达式包含一项其中决定了电流或电压趋近于零的

速率。这个比值的倒数是该电路的时间常数。

由式(4.31)可知,在零输入响应中时间常数控制电流或电压的衰减速率。图4.11所示,描绘了图4.10所示RL电路的电感电流的零输入响应曲线。

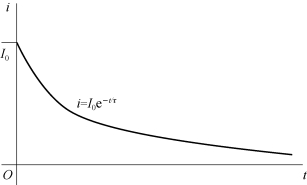
图4.11　RL电路的零输入响应曲线

如前所述,RL电路的零输入响应类似于RC电路。RL电路电感电流的零输入响应计算可分为以下几个步骤:

(1)计算电感电流换路后的初始值i L(0+)=i L(0-)=I 0;

(2)写出电路的KVL方程和电感的VCR方程构成一阶齐次微分方程;

(3)计算时间常数;

(4)求解方程,得到换路后的电感电流。