戴维南定理与诺顿定理：电路分析必知的两大定理

在电路分析中,很多时候并不需要分析电路中的每个参数,可能只要获知特定网络端口提供的电压和电流。例如,手机充电时,我们关心的是电源给充电接头提供的电压和电流,而电源电路内部的电压或电流我们并不关心。所以,可将电源内部电路进行简化。

在第2章,已经介绍了串联电路和并联电路的等效方法,但是实际电路都是由电阻、电源通过串并联混合连接在一起的,除按步进行串并联转换外,是否有其他更加简单的等效方法?

戴维南定理和诺顿定理是用来分析电路中端口网络的电路简化技术。

首先介绍戴维南定理(又称等效电压源定律),其内容是:一个含有独立电源和电阻的线性网络的两端,其对外部而言可以用一个独立电压源串联一个电阻来等效。其中,电压源的电压值v Th等于ab两端开路时的电压v oc,串联电阻的阻值R Th等于网络内全部独立电源置零时网络N的ab两端的等效电阻。如图3.12所示,是一个网络ab两端的戴维南等效电路。无论网络N的具体电路连接结构和参数如何设计,只要它们可以等效为相同的戴维南等效电路,它们在ab端为外电路提供电压和电流的能力就相同;当它们连接相同的负载时,在负载上可得到相同的电压和电流。

图3.12　电路网络N

问题3.5 画出图3.13中ab端的戴维南等效电路。

图3.13　问题3.5中的电路

解:求ab两端间的开路电压。

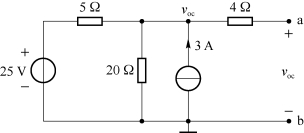
图3.14　ab端开路后,问题3.5中的电路

通过节点电压分析方法,得到

(www.xing528.com)

求得开路电压v oc=32 V。因此,戴维南等效电路中的电压源电压值v Th=v oc=32 V。

然后,去掉电路中所有电源(如图3.15所示),求出ab端间的戴维南等效电阻。

图3.15　问题3.5中电路去掉电路中所有电源,ab两端的等效电阻

由图3.15可知,ab两端的戴维南等效电阻R Th=8Ω。因此,ab端的戴维南等效电路如图3.16所示。

图3.16　问题3.5中电路的戴维南等效电路

从图3.12所示的戴维南等效电路,结合3.2节中介绍的电压源电流源的等效变换,可以将一个电压源与一个电阻的串联等效为一个电流源与一个电阻的并联,即图3.12可以等效为图3.17。其中,电流源电流值和并联电阻值也可以根据式(3.9)求出。

图3.17　诺顿定理示意图

此时,可以得到诺顿定理。

诺顿定理又称等效电流源定律,其内容是:一个含有独立电源和电阻的线性网络的两端,其对外部而言可以用一个独立电流源并联一个电阻来等效。其中,电流源的电流值i No等于ab两端短路时的电流i sc,并联电阻的阻值R No等于网络内全部独立电源置零时网络N的ab两端的等效电阻。且由电压源电流源等效变化可知与戴维南定理类似,可得无论网络N的具体电路连接结构和参数如何设计,只要它们可以等效为相同的诺顿等效电路,它们在ab端为外电路提供电压和电流的能力就相同;当它们连接相同的负载时,在负载上可得到相同的电压和电流。

利用戴维南定理或诺顿定理,可将复杂的线性电路(不含负载部分)进行简化,降低电路分析的难度。同时,这两个定理在交流电路中的应用与在直流电路中的应用完全相同,只是电阻被推广为阻抗。