间接测量方式的最大误差分析与优化

（1）被测量y为n个量的和，即

y＝x1＋x2＋x3

式中　x1、x2、x3——与被测量有关的几个已知量。

如用Δy表示被测量的绝对误差，Δx1、Δx2、Δx3代表测量x1、x2、x3时的绝对误差，可得

二端同除以y，得

我们感兴趣的是求得被测量的最大相对误差，显然它是出现在各个量的相对误差为同一符号的情况，设γ表示最大相对误差，则

式中，分别表示x1、x2、x3各量的相对误差。

【例1-2】 用安培表测量各支路电流，第一支路为15A，γ1＝±2％，第二支路为25A，γ2＝±3％，求电路总电流和可能的最大相对误差为多少？

图1-11　例题图

解：如图1-11所示，得

I＝I1＋I2＝15＋25＝40（A）

最不利的情况是被测结果的最大相对误差取同符号，即

（2）被测量y为两个量之差，即

用上述同样方法可求出被测量可能的最大相对误差。即同样用Δy、Δx1、Δx2分别表示被测量y和已知量x1、x2的绝对误差，则

考虑到最不利情况是Δx1、Δx2取相同符号，Δy＝|Δx1|＋|Δx2|则

将y＝x1－x2代入式（1-32）得

可见被测结果为两量之差时，可能的最大相对误差不仅与各个测量结果的相对误差γ1、γ2有关，而且与两个已知量之差有关。若两量之差越大，被测量可能的最大相对误差越小，反之两量之差越小，则相对误差就会增大。故通过两个量之差求被测量的方法应尽量少用。

【例1-3】 如图1-12测得第一支路电流I1和总电流I分别为I＝30A，γ＝±2％；I1＝20A，γ1＝±2％，求I2时可能的最大相对误差。

图1-12　例题图

解：I2＝I－I1＝30－20＝10（A）

若I＝30A，γ＝±2％，I1＝5A，γ＝±2％，则

可见两量相差越小，可能出现的相对误差越大。

（3）被测量y为n个量的积，即(www.xing528.com)

式中，x1、x2、x3为直接测得的已知量，n、m、p为x1、x2、x3的指数，可能为整数、分数、正数或负数。对上式两边取自然对数得

两边微分

式中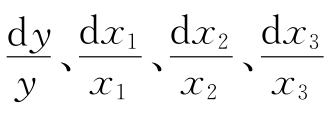，分别为被测量和各量的相对误差，取最不利的情况，即都取正值

显然被测量为n个量之商时，其情况与积的结论相同。因为时同样得

【例1-4】 用间接法求某一电阻消耗的电能，设测量电压U的相对误差为±1％，测量电阻r的相对误差为±0.5％，测量时间t的相对误差为±1.5％，求计算电能W的可能最大相对误差。

解：电能计算公式为

W＝U2r－1t

γW＝nγU＋mγr＋pγt＝2×1％＋1×0.5％＋1×1.5％＝4％

【例1-5】 测量三相交流电路的功率P、电压U和电流I，其相对误差分别为γP＝±1.5％，γU＝±1％、γI＝±1.2％，求计算功率因数cosφ的可能的最大相对误差。

解：求功率因数的公式为

【例1-6】 求通过测量振荡回路的电感L和电容C，以便间接计算角频率为ω时可能的最大相对差。设：测量电感L时相对误差γL＝±1％，测量电容C时相对误差γc＝±0.5％。

解：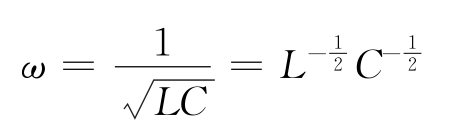

可见用这种方法测频率是有利的。

【例1-7】 试估计用伏安法测温升时可能的最大相对误差，假设电流表和电压表的准确度都是0.5级，而温度较高时电阻rH与温度较低时电阻rL的比值为1.4。

解：温升公式如下（式中α为电阻温度系数）

用伏安法测电阻的可能的最大相对误差γr为

γr＝UI－1＝1×0.5％＋1×0.5％＝1％

测热态电阻rH与冷态电阻rL之差时，可能的最大相对误差可由下式求得，因，则

最后求得温度的最大相对误差为

可见用伏安法测电阻来确定温升时的误差很大，最大相对误差为仪表误差的10倍以上，若改用0.2级的电压表和电流表，上述方法测得的误差仍有2.8％，如采用0.1级电桥测量，即γr＝±0.1％，则