偶然误差的特征及其正态分布曲线

偶然误差也称随机误差，这是一种大小、符号都不确定的误差，这种误差是由周围环境的偶发原因引起的，因此无法加以消除，但这种误差具有以下几个特征。第一，在一定测量条件下，随机误差的绝对值不会超过一定界限，即所谓有界性；第二，绝对值小的误差出现的机会多于大的误差，即所谓单峰性；第三，当测量次数足够多时，正误差和负误差出现的机会基本相等，即所谓对称性。如果用δ表示误差，用f表示误差出现次数，δ和f的关系如图1-10曲线所示。这个曲线称为随机误差正态分布曲线。

图1-10　随机误差正态分布曲线

由于随机误差具有以上这些特性，所以在工程上可以对被测量进行多次重复测量，然后用它们的算术平均值表示被测量的真值，即

式中　A——算术平均值；

n——测量次数。

如果测量次数不够多，算术平均值与真值偏离较大，因此用算术平均值表示测量结果时，其测量精度可用标准差表示，即

式中　σx——标准差。(www.xing528.com)

根据概率论原理，所谓标准差可通过均方根差σ或剩余误差为每次测量值）求出，即

应该指出，用算术平均值表示测量结果，首先要消去系统误差，因为有系统误差存在时，测量次数尽管足够多，算术平均值也不可能接近被测量真值。

例如对某一电压进行了15次测量，求得其算术平均值为20.18，并计算得出均方根差为0.34，标准差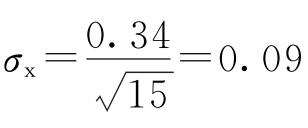，可写出其测量结果及误差评价为

A＝A±σx＝20.18±0.09

现在常用的电子计算器，都设有计算算术平均值和均方根误差的按键，利用它来处理随机误差，计算起来十分方便。