永磁同步电机调速控制系统优化

永磁同步电机（PMSM）与直流无刷电机（BLDC）电机从结构上相类似，其主要区别在于BLDC电机的转子产生的气隙磁场为梯形波，当BLDC电机以120°电角度方波电流供电时，将产生恒定的电磁转矩输出；而PMSM中永磁转子所产生的气隙磁场波形为正弦波，当定子通以三相对称的正弦波交流电流时，将产生旋转的磁场，两个磁场相互作用产生恒定的电磁转矩。如果改变定子输入的三相交流电的频率、相位、幅值，就可以改变电机输出转矩，从而对电机的转速和位置进行控制。因此其控制多采用矢量控制，与三相异步电机的矢量控制也有类似之处（7.5节已叙述过）。

由于永磁同步电机转子磁场是由永磁体产生的，因此对转子磁场的检测和定向可以直接通过转子位置传感器来实现。而且除非需要进行弱磁，转子磁链的幅值不需要控制，因此PMSM的矢量控制比异步电机的矢量控制更加简单。

1.PMSM电机数学模型

永磁同步电机的定子与普通电励磁同步电机的定子一样都是三相对称绕组。通常按照电动机惯例规定各物理量的正方向。

在建立数学模型过程中做以下基本假设：①转子永磁磁场在气隙空间分布为正弦波，定子电枢绕组中的感应电势也为正弦波；②忽略定子铁芯饱和，认为磁路线性，电感参数不变；③不计铁芯涡流与磁滞等损耗；④转子上没有阻尼绕组。

图4-18给出了一台两极永磁同步电机的结构简图。图中，规定正方向与感应电机分析时完全一样，正电压产生正电流，正电流产生正磁场，电势与磁链满足右手定则，且相电流产生的磁场轴线与绕组轴线一致，定子三相绕组轴线空间逆时针排列，A相绕组轴线作为定子静止参考轴，转子永磁极产生的基波磁场方向为直轴d轴，超前直轴90°电角度的位置是交轴q轴。并且以转子直轴相对于定子A相绕组轴线作为转子位置角θ，即逆时针方向旋转为转速正方向。先分析定子三相电压与磁链方程，然后经过坐标变换确定同步电机控制最简单的数学模型形式。

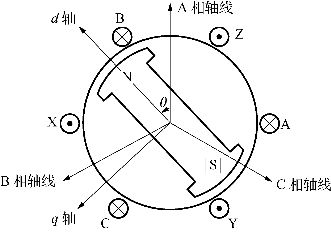
图4-18　两极永磁同步电机结构简图

1）电压平衡方程

三相永磁同步电机的定子绕组和普通三相交流异步电机或同步电机的定子绕组是相似的，三个电枢绕组空间分布，轴线互差120°电角度，每相绕组电压与电阻压降和磁链变化相平衡。所不同的是定子每相绕组内部的磁链，普通异步电机由定子三相电流与转子电流共同产生，普通同步电机由定子三相绕组与转子励磁电流和阻尼绕组电流（如果存在阻尼绕组）共同产生，而永磁同步电机的定子磁链是由定子三相绕组电流和转子永磁极产生，定子三相绕组电流产生的磁链与转子位置角有关，转子永磁极产生的磁链也与转子位置角有关，其中转子永磁极磁链在每相绕组中产生反电动势。由此得到定子电压方程式

式中，uA、uB、uC为三相绕组相电压；Rs为每相绕组电阻；iA、iB、iC为三相绕组相电流；ΨA、ΨB、ΨC为三相绕组匝链的磁链。

2）磁链方程

定子每相绕组的磁链不仅与三相绕组电流有关，而且与转子永磁极的励磁磁场和转子的位置角有关，因此磁链方程可以表示为

式中，LAA、LBB、LCC为每相绕组自感；MABA＝MBA＝MBC＝MCB、MCA＝MAC为两相绕组互感；ΨfA、ΨfB、ΨfC为三相绕组匝链的转子每极永磁磁链。

并且，有

式中，ΨfB为定子电枢绕组最大可能匝链的转子每极永磁磁链。

3）坐标变换

在交流电机分析过程中，引入了空间坐标系统的概念，主要有定子静止坐标系统、转子坐标系统、空间任意旋转坐标系统和磁场定向坐标系统等。坐标变换的理论已在7.5节叙述过，本节直接利用该理论得出结果。

当三相永磁同步电机定子绕组采用星形连接时，三相定子电流在电枢绕组中性点满足基尔霍夫电流定律，即三相电流相加等于0，因此定子电流的零轴分量等于0。这样可以得出定子电压和磁链在转子dq坐标系统中的方程可以简化为

式中，ud、uq分别为直轴和交轴等效电压；id、lid分别为直轴和交轴等效电流；Rs为每相绕组电阻；Ld、Lq分别为直轴和交轴等效电感；Ψf为定子电枢绕组最大可能匝链的转子每极永磁磁链；ω为转子角速度。

式（4-30）也可表示成

将式（4-31）代入式（4-30），用定子磁链的直轴与交轴分量来表示定子电压方程

4）数学模型求解方法

在永磁同步电机控制系统计算和仿真过程中，经常要在给定输入条件下对输出信号进行求解，输入信号简单时可以用手工计算，输入信号复杂时则只能借助于计算机仿真。

（1）对于连续正弦波电压或电流输入的永磁同步电机，电机工作在稳态过程，可直接利用坐标变换在转子dq坐标系统下的数学模型求解，也可以借助于空间矢量图求解。

（2）对于功率开关器件控制的永磁同步电机，如果转子静止，在某一逆变器状态下输入电压信号，那么可以利用阶跃或脉冲信号输入，以及电机静止状态定子两相数学模型进行计算，获得阶跃或脉冲响应。

（3）对于功率开关器件控制的永磁同步电机，通常采用三相导通控制方式，由于系统状态不断变化，因此手工计算很困难，需要利用计算机仿真。如果每一时刻三相端电压确定，感应电势主要由转子位置和速度决定，那么可以先求出三相绕组中性点电压，并计算出三相绕组的相电压和相电流，再进行坐标变换，采用转子dq坐标系统中的离散时间数学模型来建立MATLAB仿真模型，进而由计算机仿真求解。有关连续数学模型的离散化过程可以参照第4章的相关内容。

2.永磁同步电机的控制策略

永磁同步电机作为电动机运行可以进行开环或闭环控制，实现转矩（力）、转速或位置伺服控制。对于永磁同步电机开环调速驱动系统，不需要安装位置和速度传感器，只要改变供电电源频率就可以实现电机转速的调速。不过，在改变频率的过程中永磁同步电机与异步电机不同，异步电机虽然开环速度跟踪精度不高，但依靠转差运行的异步电机不存在失步的问题。也就是说，不需要转子转速与定子变频频率保持同步转速，调速过程中频率变化快慢不会影响最终的控制要求。然而，永磁同步电机则不同，定子电源频率不能改变太快。在频率调节过程中，若定子磁场的频率上升太快，则定子磁场转速增加就很快，因为转子惯量转速来不及改变，使得定转子磁场之间的相位差迅速增大，电磁转矩增大；如果定转子磁场之问的相位差超过永磁同步电机稳定运行范围后，电磁转矩反而减小。只要电磁转矩始终大于负载转矩，那么定转子磁场之间的相位差最终还是会恢复到稳定运行的范围内，永磁同步电机调速能正常进行。如果随着相位差增大，发生电磁转矩小于负载转矩的情况，那么电机转子不仅得不到加速，反而会减速，造成转子跟不上定子磁场而出现失步现象。这样定转子磁场之间的相位差由于转子减速将进一步增大，电磁转矩也由驱动变为制动，最终永磁同步电机停止运行，调速失败。

对于永磁同步电机闭环控制系统，特别是位置伺服系统都需要转子位置信息，可以避免上述失步现象的发生。转子位置信息的获取采用精度相对较高的光电编码器或旋转变压器等位置传感器，也可以采用无位置传感器的方法。为了提高永磁同步电机的控制响度速度，通常采用永磁同步电机矢量控制策略与异步电机类似，但也存在明显的不同之处。

在具体应用场合，永磁同步电机矢量控制策略根据不同的速度调节范围、性能要求还可分为如下形式：①直轴电枢电流为0的控制策略；②最大电磁转矩/电流比的控制策略；③弱磁控制策略；④最大输出功率的控制策略。

本书只介绍其中两种常用控制策略：直轴电枢电流为0和最大电磁转矩/电流比的控制策略。

1）直轴电枢电流为0的控制策略

当永磁同步电机定子电枢电流的直轴分量在控制过程中始终等于0，即id＝0时，永磁同步电机的电压方程简化为

直轴电枢电流id＝0，相当于等效直轴绕组开路不起作用。因此，如果不考虑定子直轴电压分量，仅仅从交轴电压方程可以看出，永磁同步电机相当于一台他励直流电机，定子电枢绕组中只有交轴电流分量iq、励磁磁链等与转子永磁极产生的磁链且恒定不变，等效交轴绕组中的励磁电势与转子角速度成正比。因为定子磁动势空间矢量与转子永磁体磁场空间矢量相互垂直，所以电磁转矩与交轴电枢电流成正比，即

式中，p为电机的极对数。

功率因数角ψ取决于交轴电感参数大小Lq、电驱绕组电阻Rs、永磁转子励磁磁链Ψf、转子角速度ω和负载电流大小iq。由电压方程和相量图可以得到功率因数ψ的表达式

对于直轴电枢电流等于0的控制策略，要提高功率因数必须在电机设计中采取措施，尽可能减小交轴电感参数Lq。对已经设计好的永磁同步电机（如200V、5A、Ld＝0.05H、Lq＝0.07H、Rs＝5.7Ω、Ψf＝0.9Wb）与直轴电枢电流等于0的控制策略，当交轴电枢电流额定时，转子转速在额定转速范围内与功率因数的关系如图4-19所示。

图4-19　功率因数与转子转速关糸曲线

由图4-19可以发现，交轴电流额定时存在最大功率因数为零转速，转速升高功率因数下降，但总的功率因数还是比较高。这种控制策略对于永磁同步电机来说，其转速只能在额定转速以下范围内运行，否则转子永磁磁场产生额定感应电势就会等于甚至超过端电压，最终无法作为电动机运行。

直轴电枢电流等于0的控制策略算法简单，控制灵巧，因此在永磁同步电机控制系统中应用广泛。

2）最大转矩/电流比的控制策略

直轴电枢电流等于0的控制策略简单但存在两个缺点：一方面永磁电机本身气隙磁阻不均匀，忽略了磁阻转矩的作用，使得单位电流电磁转矩不是最大；另一方面电机只能在额定转速以下工作。最大转矩/电流比的控制策略也称为单位电流转矩最大控制策略，它是凸极式永磁同步电机常用的控制策略之一。在什么情况下可以获得单位电枢电流产生的电磁转矩最大呢？根据电磁转矩与电枢电流的直轴与交轴分量的关系得到(www.xing528.com)

为了便于分析，引入电枢电流空间矢量与直轴位置的相位角γ，也就是定子电枢合成磁势幅值位置与转子直轴位置之间的夹角。这时电枢电流的两个分量与空间矢量幅值之间的关系为

将式（4-38）代人式（4-37）可以得到

首先根据上式可以确定单位电流电磁转矩关于电流相位角的函数关系

并经过整理后得到

接着，确定满足单位电流电磁转矩最大的条件。因为单位电流电磁转矩表达式（4-41）表明函数f（γ）是连续可微函数，因此存在最大值。如果函数f（γ）中认为电枢电流幅值固定，那么令单位电流电磁转矩函数f（γ）对电流相位角γ的偏微分等于0，即

即

由上式可以得到单位电流电磁转矩最大时电枢电流与相位角的关系

于是，直轴电枢电流分量可以用交轴电枢电流分量来表示

将式（4-45）代入式（4-37），可以得到单位电枢电流电磁转矩最大条件下电磁转矩与交轴电流分量的关系

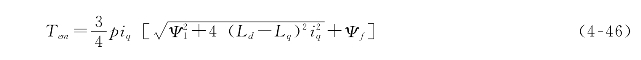
当永磁同步电机转子气隙磁导率均匀时，类似于隐极式同步电机。如果电枢绕组直轴与交轴电感参数相同，即Ld＝Lq，则可得到cosγ＝0，再由式（4-45）得到直轴指令电流id＝0，此时可得到电磁转矩，电枢电流只有交轴分量，单位电流转矩最大控制策略与直轴电枢电流等于0的控制策略完全一样。

当永磁同步电机气隙磁导不均匀时，类似于凸极式同步电机。如果直轴电感参数小于交轴电感参数，即Ld＜Lq，则由式（4-45）可知，直轴电枢电流分量小于0，电枢反应起去磁作用。与直轴电枢电流等于0的控制策略相比，交轴电枢电流分量要小一些，这种单位电流电磁转矩最大的控制策略是以削弱转子励磁磁场，提高电机功率因数的方法来提高单位电流电磁转矩的。当电机转速超过额定转速时，这种控制策略因为能削弱转子磁场，成为弱磁控制方式，可以提高出力，扩大调速范围。

如果直轴电感参数大于交轴电感参数，即Ld＞Lq，则由式（4-45）可知，直轴电枢电流分量大于0，电枢反应起助磁作用。与直轴电枢电流等于0的控制策略相比，这种单位电流电磁转矩最大的控制策略是以增强转子励磁磁场，提高电机功率因数的方法来提高单位电流电磁转矩的。当电机转速超过额定转速时，这种控制策略因为要增强转子磁场，因此无法正常运行。

3.永磁同步电机的调速控制系统实例

1）主电路

三相逆变器主电路为永磁同步电机（PMSM）供电，如图4-20所示。MCU的PWM模块提供6路：PWM信号分别控制逆变器的3个桥臂（由6个IGBT功率管构成）。该主电路与异步电机控制的主电路和BLDC电机控制的主电路完全相同。

图4-20　三相逆变器主电路

2）控制算法

本实例采用的永磁同步电机采用表贴永磁体转子结构（Ld＝Lq＝La），适合采用直轴电枢电流id＝0的矢量控制方法。

由于表贴式永磁同步电机的Ld＝Lq＝Lq，可以将式（4-32）改成如下所示的状态方程（微分方程）：

上式表示用dq轴电枢电压ud、uq可以控制dq轴电枢电流id、iq。由于Ψf为定子电枢绕组最大可能匝链的转子每极永磁磁链，ωΨf是永磁体磁链在电枢绕组中感应的旋转电动势，因此是不可控的。

由式（4-35）可知，在直轴电枢电流id＝0的控制策略下转矩方程式为：。

系统的运动方程式为

式中，J为系统的转动惯量，J＝JM＋JL（JM为电机的转动惯量，几为负载的转动惯量）；ω为电机输出轴的机械角速度；TL为负载转矩。

根据式（4-35）、式（4-47）和式（4-48）可以得到图4-21所示的dq坐标系下永磁同步电机的控制框图。

图4-21　dq坐标系下永磁同步电机的模型框图

永磁同步电机能检测的信号都是静止坐标系的参数，参数如下：直接加在永磁同步电机绕组上的是逆变器输出的三相电压uA、uB、uC；三相电流iA、iB、iC；转子磁极的位置θ；转子角速度ω。根据7.5节矢量控制的坐标变换的理论可知：uA、uB、uC和ud、uq是等价的；iA、iB、iC和id、iq是等价的。同理，控制器中的给定值是等价的；是等价的。

在调速控制系统中，需要控制永磁同步电机的转矩，使其能够快速响应，因此电流的反馈控制必不可少。Gid（s）、Giq（s）分别为直轴和交轴的电流控制环的传递函数。电流环控制一般采用比例积分（PI）控制。

把电流控制环作为内环、转速环作为外环的永磁同步电机双闭环调速控制系统，通常把电流环的响应设计得足够高，相对于外环（转速控制环）可以看成是个跟随控制，这样可以提高转速控制环的快速性和稳定性。Gω（s）为转速控制环的传递函数。转速环控制一般也采用比例积分（PI）控制。在图4-21的基础上加上双闭环（转速环、电流环）控制器的调速控制器结构框图如图4-22所示。

图4-22中，由于采用直轴电枢电流id＝0的矢量控制方法，故直轴电枢电流的给定值＝0。对转矩的控制实际上是对d、q轴电流的控制，而对电流id、iq的控制，是通过控制d、q轴电压ud、uq实现的。

由于永磁同步电机的d、q轴之间存在相互干涉的旋转电动势，旋转电动势对id、iq的控制产生影响，是不能直接对其控制的。于是，可以考虑先求出旋转电动势，然后通过控制，使其抵消掉，即采用解耦控制，消除旋转电动势对电流控制产生的影响。虽然旋转电动势ωLaiq和ω（Ψf＋Laid）不能直接检测出来，而ω、id、iq却可以检测出来，又由于La和Ψf是常数，可以事先测定，因此旋转电动势可以在控制回路中通过计算求得。

通过解耦控制，在旋转电动势耦合项中引入电机转速和电机参数的因素，可以合理地对电压值进行调节，即无论被控电机的转速高低和电机参数的大小，都可以通过实时计算旋转电动势耦合项得到准确的d、q轴电压指令值，从而能够精确地控制d、q轴电流，可以使控制系统实现对不同参数下永磁同步电机的高精度调速控制要求。

图4-22双闭环（转速环、电流环）控制器的结构框图

3）调速控制系统构成

图4-23为永磁同步电机调速控制系统的结构框图，其主要由以下4部分组成：①功率变换电路（主电路）；②表贴式永磁同步电机；③定子电流、转子位置及转子转速传感器；④控制电路。

图4-23　永磁同步电机调速控制系统的结构框图

图4-23中，控制电路为采用基于单片机为控制芯片的电子控制单元（ECU），控制电路实现以下功能：定子电流、转子位置及转子转速传感器信号的输入处理电路；坐标变换计算；速度环、电流环控制及解耦算法；PWM占空比调制；驱动电路等。

整个调速控制系统的控制过程：过速度指令与电机当前的转速相比较，经过速度环控制器，输出电磁转矩指令值，通过电磁转矩方程，求得q轴电流iq的指令值同时控制d轴电流id＝0。检测输入到永磁同步电机三相绕组中的电流，利用三相到两相的坐标变换式变换得到d、q轴上的电流id、iq，将其同给定的d、q轴电流相比较，通过各自的电流控制器，利用d、q轴下的电压方程式和解耦控制器的输出得到d、q轴电压指令值。最后，通过两相到三相的坐标变换，将变换后得到的三相电压瞬时值指令通过六路PWM信号输入到三相逆变器中，产生三相正弦电流并输入到永磁同步电机的定子绕组中，实现对永磁同步电机的调速矢量控制。