双线圈励磁的铁芯如图3-10所示,铁芯上装有线圈A和B,匝数分别为NA和NB。主磁路由铁芯磁路和气隙磁路串联构成,两段磁路的断面面积均为s。假设外加电压uA和uB为任意波形电压,励磁电流iA和iB也为任意波形电流,图中给出了电压和电流的正方向。
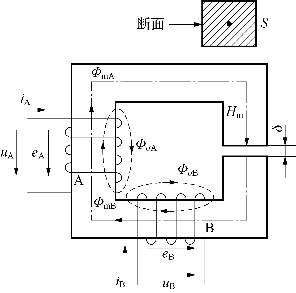
图3-10 双线圈励磁的铁芯
1.单线圈励磁
先讨论仅有线圈A励磁的情况。当电流iA流入线圈时,便会在铁芯内产生磁场。根据安培环路定律,有

式中,H为磁场强度,A/m;∑i为该闭合回线包围的总电流,A。
在图3-10中,取铁芯断面的中心线为闭合回线,环行方向为顺时针方向,根据安培环路定律,若电流正方向与闭合回线的环行方向符合右手螺旋关系时,i便取正号,否则取负号。沿着该闭合回线,假设铁芯磁路内的Hm处处相等,方向与积分路径一致,气隙内Hδ也如此。于是,有
![]()
式中,lm为铁芯磁路的长度,m;δ为气隙长度,m;NA为线圈A的匝数;fA为磁路的磁动势,A。Hmlm和Hδ为磁压降,并表明线圈A提供的磁动势fA被主磁路的两段磁压降所平衡。此时,fA相当于产生磁场H的“源”,类似于电路中的电动势。
在铁芯磁路内,磁场强度Hm产生的磁感应强度Bm为
![]()
式中,μFe为铁芯磁导率,H/m;μr为相对磁导率,H/m;μ0为真空磁导率,H/m。
在气隙磁路内,磁场强度Hδ产生的磁感应强度Bδ为
![]()
式中,μ0为真空磁导率,H/m。
将式(3-38)和式(3-39)代入式(3-37),可得

若不考虑气隙δ内磁场的边缘效应,气隙内磁场Bδ也均匀分布,于是式(3-40)可写为

式(3-41)中的各物理量可以定义为
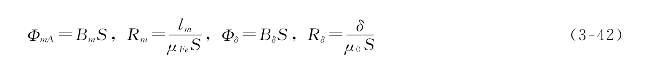
式中,ΦmA为铁芯磁路主磁通,Wb;Rm为铁芯磁路磁阻,1/H(每亨[利]);Φδ为气隙磁通,Wb;Rδ为气隙磁路的磁阻,1/H。
由于磁通具有连续性,显然有ΦmA=Φδ,则有Bm=Bδ。于是根据式(3-41)可得
![]()
式中,Rmδ为串联磁路的总磁阻,1/H。
通常,磁阻的倒数定义为磁导,即A=1/R,磁导的单位为H(亨)。则磁路的欧姆定律有另外一种表达方式:
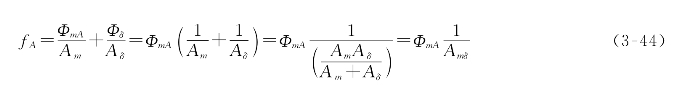
式(3-43)和式(3-44)表明,作用在磁路上的总磁动势恒等于闭合磁路内各段压降之和,这就是磁路的欧姆定律。
对图3-10所示的磁路而言,尽管铁芯磁路长度比气隙磁路长得多,但由于μFe远大于μ0,气隙磁路的磁阻还是要远大于铁芯磁路的磁阻。对于这个具有气隙的串联磁路,总磁阻将取决于气隙磁路的磁阻,磁动势大部分将降落在气隙磁路中。在很多情况下,为了问题分析的简化,可将铁芯磁路的磁阻忽略不计,此时磁动势fA与气隙磁路磁压降相等,即有
![]()
图3-10中,因为主磁通ΦmA是穿过气隙后而闭合的,提供了气隙磁通,所以又将ΦmA称为励磁磁通。定义线圈A的励磁磁链为
![]()
由式(3-37)、式(3-43)和式(3-46),可得
![]()
定义线圈A的励磁电感LmA为

LmA表征了线圈A单位电流产生磁链ΨmA的能力。对于图3-10的具体磁路,又将LmA称为线圈A的励磁电感。LmA的大小与线圈A匝数的二次方成正比,与串联磁路的总磁导成正比。由于总磁导与铁芯磁路的饱和程度(μFe)有关,因此LmA便是一个与励磁电流iA相关的非线性参数。若将铁芯磁路的磁阻忽略不计(μFe=∞),LmA便是一个仅与气隙磁导和匝数有关的常数,即有LmA=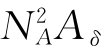 。
。
在磁动势fA作用下,还会产生没有穿过气隙主要经由铁芯外空气磁路而闭合的磁场,称为漏磁场。它与线圈A交链,产生漏磁链ΨσA,可表示为
![]()
式中,LσA为线圈A的漏电感,m H。LσA表征了线圈A单位电流产生漏磁链ΨσA的能力,由于漏磁场主要分布在空气中,因此LσA近乎为常值,且在数值上远小于LmA。
线圈A的总磁链为
![]() (https://www.xing528.com)
(https://www.xing528.com)
式中,ΨAA为线圈A中电流iA产生的磁场链过自身线圈的磁链(称为自感磁链),Wb,LA为自感(由漏电感LσA和励磁电感LmA两部分构成)。这样,通过电感就将线圈A产生磁链的能力表现为一个集中参数。在以后的分析中可以看出,电感是非常重要的参数。
当励磁电流iA变化时,磁链ΨAA将发生变化。根据法拉第电磁感应定律,ΨAA的变化将在线圈A中产生感应电动势eAA。若设eAA的正方向与iA的正方向一致,iA的方向与ΦmA的方向之间符合右手法则,则有
![]()
根据电路的基尔霍夫第二定律,线圈A的电压方程为

由式(3-51)和式(3-52)可得,在时间dt内输入铁芯线圈A的净电能d WeAA为
![]()
在没有任何机械运动的情况下,由电源输入的净电能dWeAA将会全部变成磁场能量的增量d Wm,于是
![]()
设磁路的Ψ—i曲线如图3-11所示。
当磁通是从0增长到ΦmA时,相应地线圈A磁链由0增长到ΨAA,根据图3-11的Ψ—i曲线,图中阴影部分的面积是磁路的磁场能量,即磁能Wm,则有
![]()
显然,图3-11中的Ψ—i曲线为非线性。若忽略铁芯磁路的磁阻和漏磁场的漏磁,Ψ—i曲线便是一条直线,即图3-11的曲线改成直线后重新计算阴影部分面积,则磁能Wm为
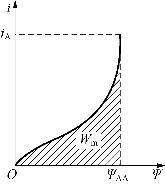
图3-11 磁路的Ψ—i曲线

在一定磁感应强度下,介质的磁导率μ越大,磁场的储能密度就越小,否则相反。对于图3-10所示的电磁装置,由于μFe远大于μ0,因此,绝大部分磁场能量Wm将储存在气隙中。
2.双线圈励磁
对于图3-10所示的电磁装置,现分析线圈A和线圈B同时励磁的情况。此时忽略铁芯磁路磁阻,磁路为线性,故可以采用叠加原理,分别由磁动势fA和fB计算出各自产生的磁通。
同线圈A一样,可以求出线圈B产生的磁通如ΦmB和ΦσB,此时线圈B的自感磁链ΨBB为
![]()
式中,LσB为线圈B的漏电感;LmB为线圈B的励磁电感;LB为线圈B的自感。
线圈B产生的磁通同时要与线圈A交链,反之亦然。这部分相互交链的磁通称为互感磁通。在图3-10中,励磁磁通ΦmB全部与线圈A交链,则电流iB在线圈A中产生的互感磁链ΨAB为
![]()
定义线圈B对线圈A的互感为LAB,则由式(3-58)可得LAB为
![]()
同理,线圈A对线圈B的互感LBA与线圈B对线圈A的互感为LAB相等,即
![]()
在图3-10中,当电流iA和iB的方向同为正时,两者产生的励磁磁场方向一致,因此两线圈互感为正值。若改变iA或iB的正方向,或者改变其中一个线圈时绕向,则两者的互感便成为负值。值得注意的是,如果NA=NB,则有LmA=LmB=LAB=LBA,即两线圈不仅励磁电感相等,且励磁电感又与互感相等。
线圈A的全磁链ΨA可表示为
![]()
同理,线圈B的全磁链ΨB可表示为
![]()
感应电动势eA和eB分别为

在时间dt内,由外部电源输入铁芯线圈A和B的净电能d We为
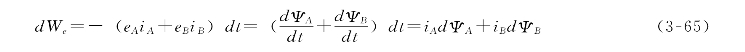
由电源输入的净电能d We将全部转化为磁场能量的增量d Wm,即有
![]()
当两个线圈的磁链由O分别增长为ΨA和ΨB时,整个电磁装置的磁场能量Wm为
![]()
因为磁路为线性,则有
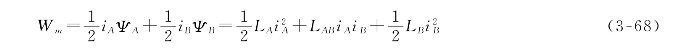
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




