待切削层金属的塑性侧流沿刀尖圆弧两侧进行,会在已加工表面最大残留高度R′max刀纹两侧,各形成一个高度为h的附加凸峰,称为塑性侧流凸峰,如图7-10所示。此时,车削表面最大残留高度为

形成的塑性侧流凸峰使已加工表面上残留高度发生畸变,这是影响加工表面粗糙度形成的一个非几何学因素,会增大已加工表面的表面粗糙度值。
设刀尖为刚性体,工件在刀具挤压和切削热耦合作用下,产生塑性变形的同时,也存在着刀具挤压后的弹性变形回复。则塑性侧流凸峰高度可表示为
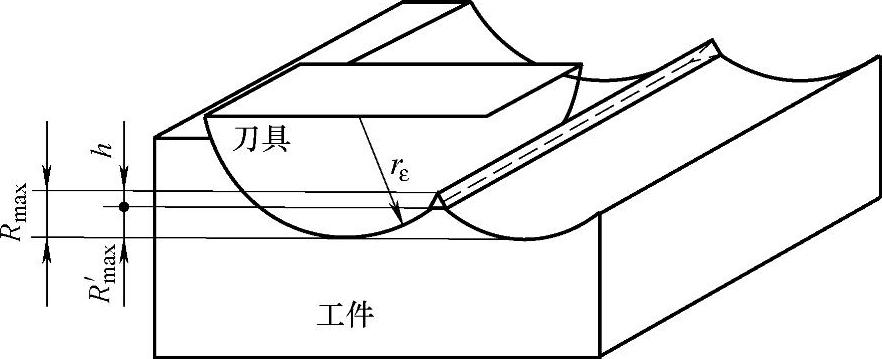
图7-10 塑性侧流凸峰示意图
h=Δhp-Δhe (7-2)
式中,Δhp为刀具挤压作用下的塑性变形高度(mm),Δhe为刀具挤压后的弹性变形回复高度(mm)。
刀具挤压作用下的塑性变形高度Δhp的计算,可参照Kragelskii-Dru-janov摩擦磨损计算方程[131]:
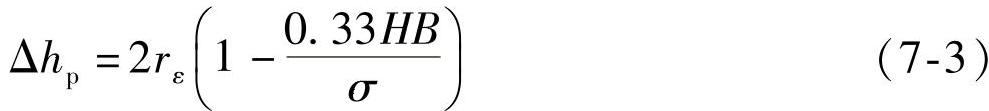 (https://www.xing528.com)
(https://www.xing528.com)
式中,rε为刀尖圆弧半径(mm),HB为工件材料的硬度,σ为工件材料变形过程中的流动应力(MPa)。
根据John Cook材料模型,流动应力可表示为[132]
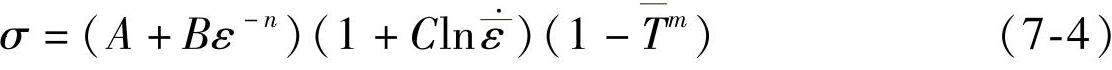
式中,σ为流动应力(MPa);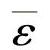 为等效塑性应变(mm/mm);A、B和n分别为应变常量(MPa)、应变硬化系数(MPa)和应变指数;
为等效塑性应变(mm/mm);A、B和n分别为应变常量(MPa)、应变硬化系数(MPa)和应变指数;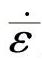 为等效塑性应变率((mm/mm)/s),C为应变率系数;T为切削平均温度(℃);m为温度指数。
为等效塑性应变率((mm/mm)/s),C为应变率系数;T为切削平均温度(℃);m为温度指数。
刀具与工件的接触,可以看成是半径为rε的刚性球与平面的接触,参照Hertz弹性接触理论[133],刀具挤压后的弹性变形回复高度为

式中,E为工件材料的弹性模量(MPa),Fy为垂直于工件表面的切削分力(N)。
将式(7-3)~式(7-5)带入式(7-2),得金属切削加工表面的塑性侧流凸峰高度
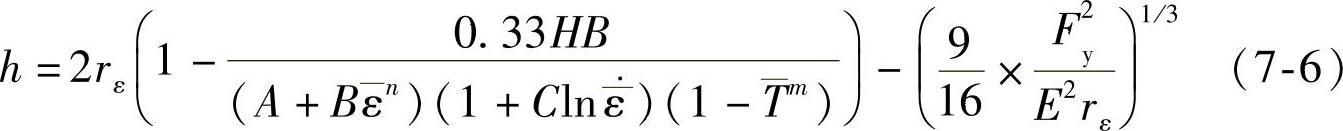
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




