硬态切削系统稳定性极限的数值仿真方法优化

淬硬钢精密切削系统稳定性极限分析表明，在实际加工前，对系统的动力学参数进行识别，根据式（5-14）、式（5-15）即可求得极限切削宽度b_lim，实现对切削系统稳定性进行预测。

基于上节的稳定性极限分析，应用Matlab数值模拟的方法预测硬态切削系统的稳定性极限，流程图如图5-3所示。首先，识别振动系统动力学参数刚度系数k、主振系统固有频率ω_n、阻尼比ζ和切削过程的动力学参数切削刚度系数k_c、方向系数u，确定刀尖圆弧半径r_ε，并选取振动频率ω的范围和步长，再依次取不同J值，计算不同转速n下对应的硬态切削极限稳定切削宽度b_min，最后可绘制出切削系统稳定性极限预测图。

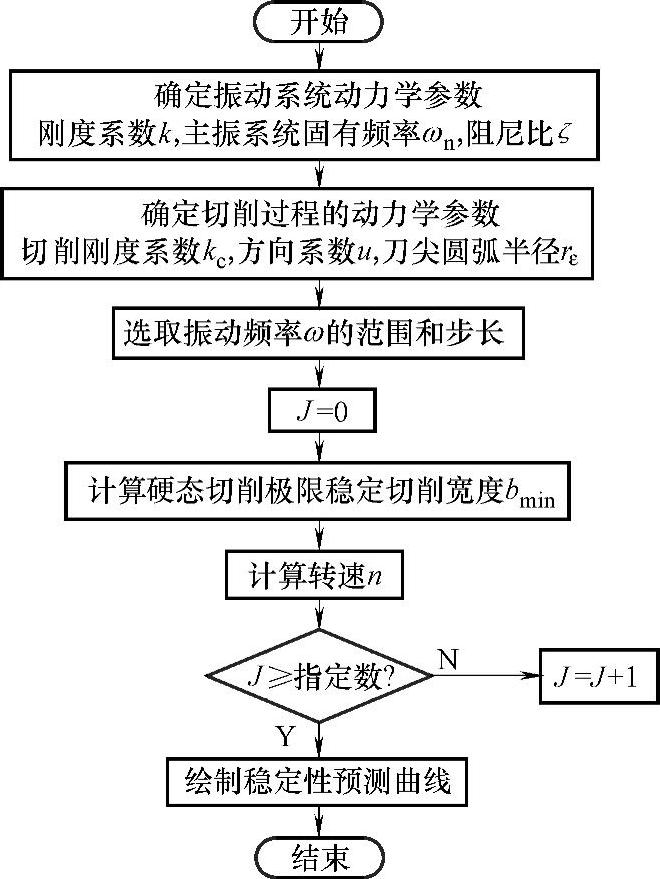
图5-3 硬态切削系统的稳定性极限预测流程图(www.xing528.com)

在刚度系数k=11389.9N/mm、主振系统固有频率ω_n=500×2πrad/s、阻尼比ζ=0.07、切削刚度系数k_c=10000N/mm²、方向系数u=0.42、刀尖圆弧半径r_ε=1.2mm的条件下，确定了合理的振动频率ω并选取其步长为5πrad/s，用Matlab数值仿真模拟出了硬态切削系统的稳定性极限预测数值仿真图，如图5-4所示。J依次取值，每一个J值对应一个耳垂线，该线即为不同转速n下对应的极限稳定切削宽度b_lim。在耳垂线下部区域，振动系统动力学模型的特征方程根s的实部σ＜0，系统处于稳定状态，即为切削的稳定区；在耳垂线上部区域，振动系统动力学模型的特征方程根s的实部σ＞0，系统处于不稳定状态，该区域为切削的不稳定区，将会发生激烈的切削振动；在（b_lim）_lim=0.3644mm虚线下部区域，无论刀具条件如何变化，都会是稳定切削区，即无条件稳定区，而（b_lim）_lim=0.3644mm虚线上与耳垂线线下的区域，只有在特定转速和刀具条件下，才会成为稳定切削区，即有条件稳定区。

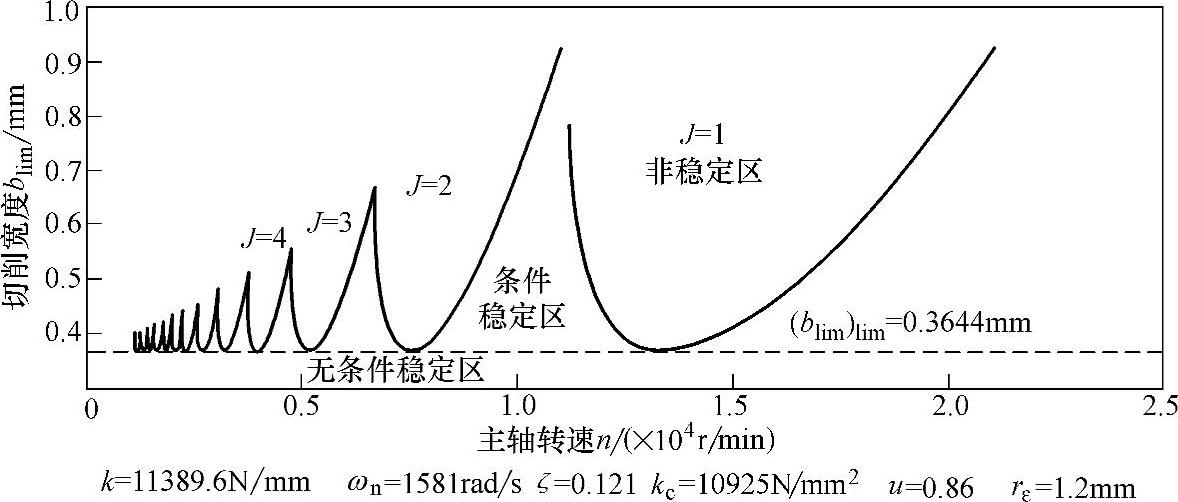
图5-4 硬态切削系统的稳定性极限预测数值仿真图