金属切削中的模态耦合自激振动探析

试考虑―镗杆，其横截面为长方形，在其端部装有刀夹与镗刀，如图3-21a所示。刀夹连同镗刀可在x₁、x₂两个相互垂直的方向上振动。设镗杆（可视为一悬臂梁）在此两方向上的刚度系数分别为k₁与k₂，由图可见

k₁＜k₂ （3-85）

设刀夹连同镗杆的等效质量为m，该振动系统的简图可用图3-21b来表示。图中y轴为工件上被切削表面的法线方向，切削厚度s₀即在此方向上测量。F=F₀+ΔF为刀具所受切削力。

图3-21 镗杆及其振动系统简图

如果不考虑切削力的作用，此系统的运动方程为

这是两个独立的单自由度系统的运动方程，其间无耦合。此外，此例中两个自由度的质量均为m。下面就会看到，正是切削力的作用，使这两个自由度上的运动耦合起来，并导致自激振动。其中，切削过程仍然起着力的控制机构与位移反馈的作用。

由于切削力的作用，运动方程变为

式中，ΔF₁₁是由于x₁轴正方向的振动位移在该轴负方向引起的切削力的增量，可推导如下：设切削刃在x₁轴正向的位移量为x₁，其在y轴负向的投影为x₁cosθ，此即切削厚度的变化量Δs，Δs引起切削力的增量ΔF=a_wk_sΔs=a_wk_sx₁cosθ，假定ΔF作用在平均切削力F₀的方向上，而ΔF在x₁轴负向上的投影ΔF₁₁即为

式中，a_w、k_s分别为切削宽度（或工件的厚度）和切削力的切削厚度系数，其意义与式（3-45）中同样符号的意义相同。角度θ与θ₀的意义可从图3-21b中看出。

由于ΔF₁₁的作用方向是指向x₁轴的负向，故在式（3-88）右边的ΔF₁₁前冠以负号，式（3-88）、式（3-89）右边其他负号的来源也相同。

ΔF₁₂是由于x₂轴正方向的振动位移在x₁轴负方向上引起的切削力的变化，

ΔF₂₁、ΔF₂₂的意义可类推为

需要说明的是，除了上述切削力的动态变化量ΔF_ij（i，j=1，2）以外，作用在刀具上的还有平均切削力F₀，它是由平均切削厚度s₀引起的。在式（3-88）、式（3-89）的右边并未计入F₀，这是由于图3-21b中x₁、x₂坐标系的原点O是放在F₀作用后的静平衡位置上，因而振动位移x₁、x₂是从静平衡位置开始计算的。

将式（3-90）～式（3-93）代入式（3-88）、式（3-89）的右边，并移项得

式中

(www.xing528.com)

即

可将式（3-94）、式（3-95）缩写为

式（3-98）、式（3-99）与式（3-73）、式（3-74）的一般式相同。现在按前述关于式（3-73）、式（3-74）所示系统的稳定性和自激振动的分析与结论来考查式（3-98）、式（3-99）所表示的切削系统的动态稳定性问题。式（3-83）与式（3-84）分别表示了不会出现与将会出现自激振动的条件。下面分析这两种条件之间的临界状态：

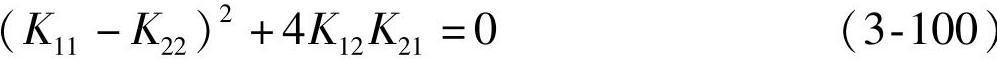
将式（3-97）代入式（3-100），可解出临界切削宽度为

式中

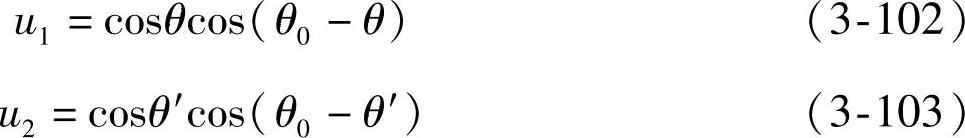
u₁和u₂分别称为x₁和x₂轴的方向系数。在给定的条件（k_s、k₁、k₂、u₁、u₂）下，如果切削宽度a_w＞a_wcr，则切削系统将会发生自激振动（振幅上升）；如果a_w＜a_wcr，则不会发生自激振动（初始振幅会因实际存在的阻尼而衰减）。

从物理意义上看，a_wcr应为正实数，为此要求式（3-101）中的

u₁u₂＜0 （3-104）

将式（3-102）、式（3-103）和式（3-96）代入式（3-104），并化简得

而为使上式满足，一定要有

0＜θ＜θ₀ （3-106）

从图3-21b可见，以上条件相当于x₁轴（即刚度较小的轴）应落在工件表面法线方向y与切削力F₀的方向之间，才可能发生自激振动，而在此角度范围之外，为虚数，a_wcr不存在，系统不会由于模态耦合而发生自激振动。在式（3-106）表示的范围内，a_wcr与θ角的关系以极坐标图表示在图3-22中。图中，工件表面的法线方向y与切削力F₀的方向及其间夹角θ₀视为不变，这也就是将工件与工具的位置视为不变。变化的是θ角，即镗杆截面刚度较小的方向（x₁轴）相对于y轴的取向角，θ在0°～θ₀的范围内，a_wcr随θ而变化，而在θ=θ₀/2时，a_wcr取极小值。在0°～θ₀以外，a_wcr不存在。

图3-22 镗杆的模态耦合稳定性图

以上结果给我们提供了一些颇具实际意义而又出乎意料的启示。首先是如何布置刀具系统的刚度主轴方向的问题：应该尽量避免将最小刚度的方向布置在F₀与y的夹角内，万不得已，也应尽可能避开θ=θ₀/2的位置。其次，式（3-101）表明，a_wcr与刚度差k₂-k₁成正比，因此圆形截面的镗杆（k₂=k₁）最容易产生模态耦合的自激振动。而对镗杆在两个相对的方向上加以削扁，使得k₁＜k₂，这样似乎是削弱了系统的刚度，但事实上只要合理布置刚性立轴的方向，反而有利于提高a_wcr，即提高系统抗模态耦合自激振动的能力，这一结论似乎与常识相悖，可是确已得到实验的验证^[124]。

在结束这一小节之前，我们来直观地说明一下金属切削过程中的模态耦合颤振的能量机理。先看图3-21b，由于自激振动，切削刃在工件中的移动轨迹为一椭圆PABCP，其长轴沿x₁轴的方向。注意到切削力F₀与ΔF的方向，可见在切削刃沿PAB切入工件时，切削力做负功；而在切削刃沿BCP切出工件时，切削力做正功。可是，切削刃在行程BCP时的切削厚度比较小，因而负功的数量较小；而在行程PAB时的切削厚度比较大，因而正功较大，正负相消，在每个振动周期中切削力都对振动系统做了净正功，这正是自激振动所赖以不断扩大的能量来源^[125]。