金属切削过程中再生颤振的优化控制

3.3.3.1 再生颤振系统

金属切削过程中发生的再生颤振是一种典型的由于振动位移延时反馈所导致的动态失稳现象，也是金属切削机床发生自激振动的主要原因之一。

图3-15是再生颤振模型。其中，机床结构被简化成一个单自由度系统，切削运动由工件的自转N与刀具沿工件径向的切削厚度s₀组成，s₀在数量上又等于平均切削厚度。x（t）是刀具相对于工件在水平方向的振动位移，即机床结构的变形，而F（t）是作用在刀具上的切削力。这里机床结构相当于图3-14中的振动体，F（t）作用在其上产生振动位移x（t）；另外x（t）又引起瞬时切削厚度s（t）围绕其均值s₀变化，而这一变化又会反过来引起切削力F（t）变化。因此，这里切削过程即成为图3-14中的力的控制机构，它按照振动位移来控制激振力，从而实现位移反馈。还必须看到，s（t）不仅与切削刃在当时的振动位移x（t）有关（图3-15中阴影部分的内表面），而且还与工件前一转时的振动y（t）有关（见图3-15中阴影部分的外表面）。由此可见，这里存在振动位移的延时反馈。

图3-15 再生颤振模型

在平稳切削条件下，工件表面上切削厚度为s₀的一层金属被均匀地切下，切削刃相对于工件的运动轨迹为阿基米德螺线，如图3-15中细实线所示；此时切削力F₀为一恒量，此力作用在机床结构上，引起恒定的变形x₀；而恒定的x₀又反过来保证切削厚度s₀恒定不变。从理论上讲，如果没有外界干扰，此平稳切削过程似乎可以一直进行下去。可是，如前所述，在实际情况下，总是存在这样或那样的扰动，因此上述平稳切削过程注定要受到扰动。如果受扰后，切削过程仍能回复到平衡状态，则过程仍然是平稳的；如果一个扰动使切削过程越来越偏离上述平衡状态，则切削过程是不稳定的。

现在假设在切削过程中突然碰到某一个干扰，例如，切削刃碰到工件材料中的某一个硬质点，切削力立即获得一个动态的增量ΔF（t），而ΔF（t）作用在机床结构上，引起振动x（t），后者又使瞬时切削厚度发生了Δs（t）的变化，从而引起切削力的二次变化ΔF′（t）。在一定的条件下，工件转动一转后，切削力的波动量会增加，即ΔF′（t）＞ΔF（t）。同理，工件再转动一转后，又会有ΔF″（t）＞ΔF′（t）……如此周而复始，ΔF及x（t）不断上升，终于形成强烈的自激振动。切削过程中的这类自激振动，称为“再生颤振”（Regenerative Chatter）。

这里要说明两点：第一，激起这一连串响应并发展成自激振动的那个“初始扰动”只作用一次，就被“遗忘”了，此后的响应是由于系统内部的“机床结构”与“切削过程”这两个矛盾着的方面相互作用而得以维持与扩大的，而与外界的扰动无关；第二，以上只是为了说明方便，才将各因素间影响的因果关系按一定的秩序来讲述，但实际上，各因素是在相互影响、相互制约中同时、连续地变化，不应该理解为一个因素改变以后，下一个才跟着变。

以下通过数学模型来分析再生颤振的机理与规律。

3.3.3.2 运动方程

按照图3-15，可以将运动方程写成

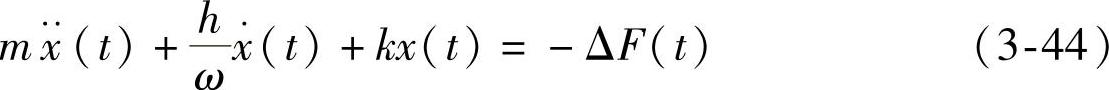
式中，h是滞后阻尼系数。这里采用滞后阻尼只是为了使后面的公式比较整齐，当阻尼比较小，而系统作简谐振动时，无论采用滞后阻尼模型或粘滞阻尼模型，其差别都不大。式（3-44）右边的负号是由于对作用在刀具上的切削力ΔF（t）的正向与工具振动位移x（t）的正向作了相反的规定，如图3-15所示。

如果切削厚度的变化Δs（t）比较小，则切削力的动态增量ΔF（t）可以表示为

式中，a_w为切削宽度（mm），即图3-15中工件的厚度（垂直于图面度量）；k_s为切削力的切削厚度系数（N/mm²）。

以下求切削厚度的动态变化Δs（t）与刀具工件之间的相对振动x（t）之间的关系。将图3-15中的阴影部分放大、展直，绘于图3-16中。图3-15中的阿基米德螺线（即平稳切削所对应的切削刃轨迹）在图3-16中被展成了两条平行直线，它们相距s₀。围绕这两条直线的波浪线（即细实线与粗实线）分别是切削刃在本圈和上一圈中的切削轨迹x（t）及y（t），它们分别构成被切削层的下表面和上表面，此两者之差即为振动切削条件下的瞬时切削厚度

s（t）=x（t）-y（t） （3-46）

图3-16 在工件相邻两转中刀具的切削轨迹

仍考虑x（t）为等幅谐波的情况，即稳定与不稳定之间的临界状态，设

于是，由图3-16有

式中，T为工件每转一转所需要的时间（s），

设β为相邻两圈切削刃波纹之间的相位差

将式（3-47）、式（3-48）和式（3-50）代入式（3-46），得

s（t）=a₀cos（ωt）-a₀cos（ωt-β）+s0

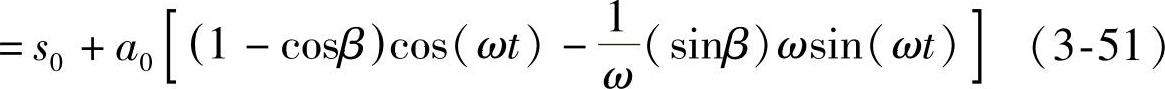
记

并考虑到式（3-47）及

得

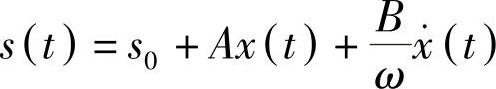
而切削厚度围绕其均值s₀的动态变化为

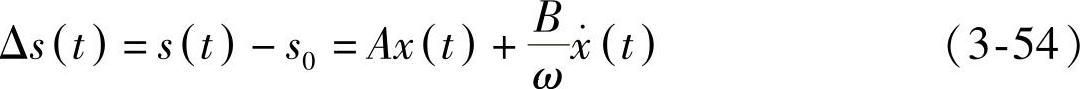
将式（3-54）代回式（3-45），即得动态切削力的表达式

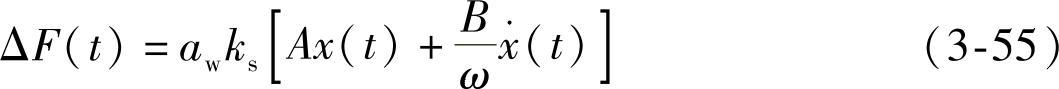
此式明确表示激振力同时受到振动位移和振动速度的控制，再一次证明了位移的延时反馈相当于位移与速度同时反馈。

将式（3-55）代入运动方程即式（3-44），并移项得

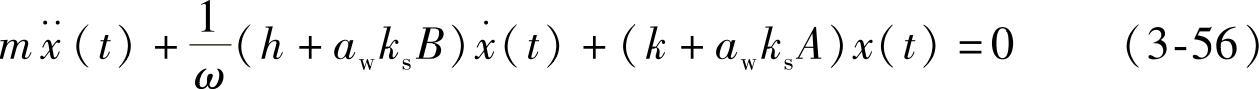
这是一个单自由度系统自由振动的运动方程，其刚度系数与阻尼系数均由两部分组成：一部分是机床结构本身的刚度或阻尼，而另一部分则是由于位移延时反馈，即“再生效应”造成的切削过程的等效刚度与等效阻尼。(www.xing528.com)

由式（3-52）知A≥0，且通常有a_wk_sA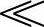k，即切削过程的等效刚度为正，且远远小于机床结构本身的刚度。由此看来，等效刚度只可能使系统的总刚度略有增加，对系统的特性并无实质性的影响。可是另一方面，等效阻尼a_wk_sB却有可能使整个切削系统失去动态稳定性。首先，由式（3-52），β可正可负，视β角而定，当β=180°～360°时，B=sinβ＜0，因此等效阻尼a_wk_sB是负的；其次，如果切削宽度a_w又足够大，则可使h+a_wk_sB＜0，即系统的总的阻尼成为负的，从而发生自激振动。

根据以上分析，可得再生颤振系统的框图如图3-17所示。

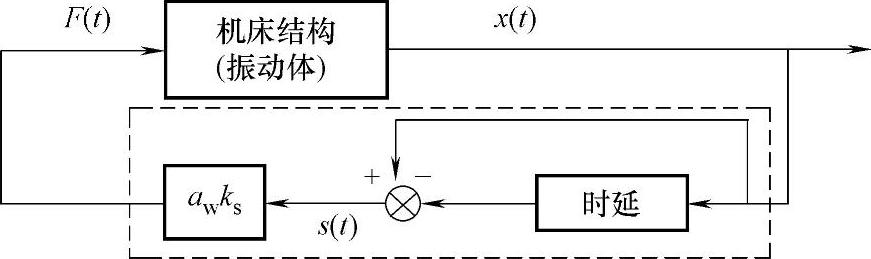
图3-17 切削过程中的再生颤振系统框图

3.3.3.3 稳定性方程与稳定性图

在上述模型中，工件转速N与切削宽度a_w是两个主要的工艺参数。这里基于运动方程来分析工艺参数对切削系统稳定性的影响。

我们是在研究等幅振动，即稳定与不稳定之间的临界状态，为此，式（3-56）中的总的阻尼系数应该为零，即

h+a_wk_sB=0 （3-57）

由此可求出临界切削宽度

当a_w＞a_wcr时，系统的总阻尼变为负值，将会发生自激振动。因此，a_wcr被称为“稳定性阈”。

在满足式（3-57）的条件下，式（3-56）变为

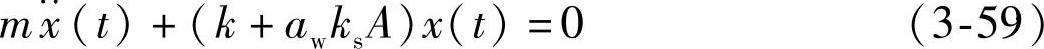
这是无阻尼系统自由振动的运动方程，其固有频率为

或写成

式中，ω为系统自激振动的颤振频率；ω₀是机床结构本身的固有频率。显然ω＞ω₀，即自激振动的频率总是略高于机床结构某个失稳模态的固有频率。这是由于切削过程的等效刚度使得整个切削系统的刚度略有上升引起的。

式（3-57）和式（3-61）构成该系统的稳定性方程组

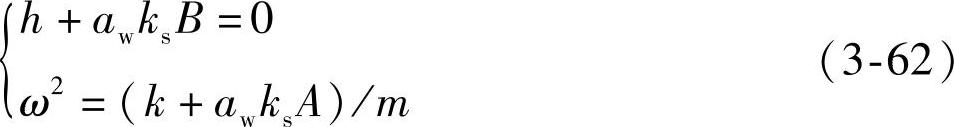
式中，

当机床结构的动态特性m、h、k与切削过程的特性k_s给定以后，由式（3-62）可解出在某一转速N下发生颤振的临界切削宽度a_wcr，及在该临界条件下的颤振频率ω。显然a_wcr及ω都与工件的转速N有关，表示这种关系的图线称为系统的“稳定性图”（Stability Chart）。图3-18给出了典型的稳定性图，图3-18a中具有耳垂状的阴影区是不稳定区域，而水平虚线以下的区域是在所有工件转速下均属稳定的无条件稳定区。当式（3-58）中的sin（60ω/N）=-1时，得最小的临界切削宽度

a_wcrmin=h/ks （3-65）

此即图3-18a中的无条件稳定区域的宽度。当a_w＜a_wrmin时，切削系统在任何工件转速N下均为稳定。

图3-18b显示出在稳定性阈上（a_w=a_wcr时），颤振频率w与工件转速N之间的关系呈齿状。

3.3.3.4 负阻尼的成因及其作用

再生颤振在β=180°～360°时，切削过程的等效阻尼是负的。下面较为详细地分析一下负阻尼的成因及其作用。

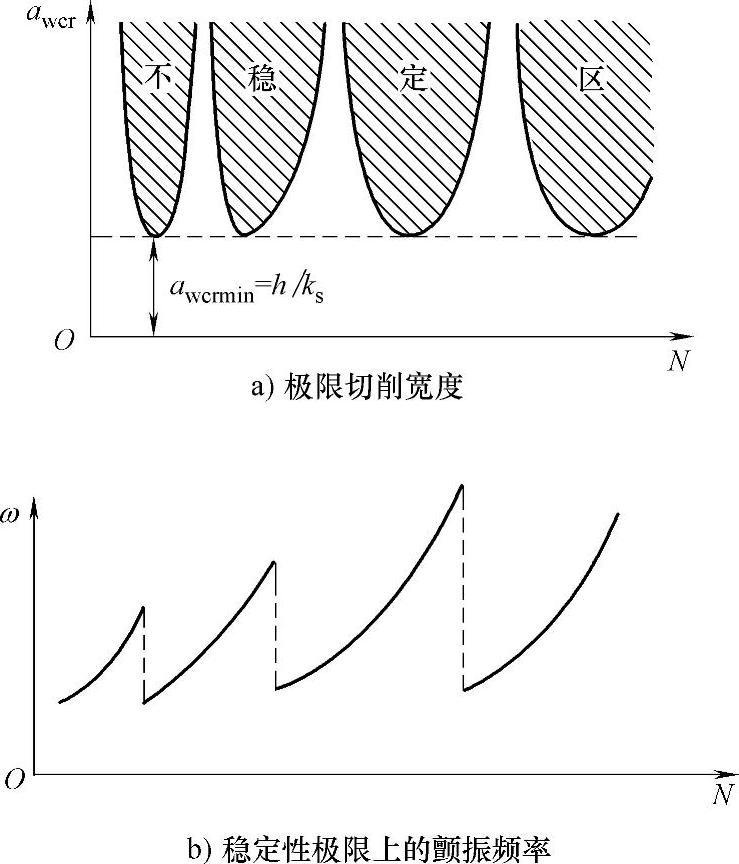
图3-18 稳定性图

图3-19分别给出了振动切削条件下β=90°与β=270°两种情况的被切削层的图形。其中图3-19a为β=90°时的情况，图中上下两波纹线之间的距离为瞬时切削厚度s（t）=x（t）-y（t），而s（t）=s₀+Δs（t），即为均值s₀及围绕均值的波动Δs（t）两部分之和。可能激起振动的是Δs（t）这一部分，而s₀产生一恒力，只能引起系统平衡位置的变动。为了从图上消除s₀，可将曲线y（t）向下平移一个距离s₀，得到虚线所示的曲线y′（t），y′（t）与曲线x（t）之间的距离即为Δs（t）。这里需要说明，切削厚度s（t）只能是正的，但Δs（t）却可正可负，当y′（t）在x（t）之上时，Δs（t）＞0；反之Δs（t）＜0。同样，切削力F（t）也不可能是负的（其正向如图3-15所示）。可是从式（3-45）可知，由于Δs（t）的符号可变，切削力的动态分量ΔF（t）亦可正可负。按图3-15中规定的切削力F（t）的正向可知，正的切削力会把刀具从工件推开，而负的切削力则倾向于把刀具拉向工件。另外从图3-19a可见，在一个运动周期中，刀具的运动轨迹可分为切出与切入两个阶段，在切出阶段刀具退出工件，而在切入阶段刀具趋向工件。当β=90°时，在切出阶段的大部分时间内，Δs（t）＜0，因而ΔF（t）＜0，即动态切削力力图把刀具拉向工件；而在切入阶段的大部分时间内，Δs（t）＞0，因而ΔF（t）＞0，即动态切削力力图将刀具从工件中推开。动态切削力的方向与刀具运动速度的方向的这种关系如图3-20a所示，从图中可见，当β=90°时，动态切削力ΔF的方向基本上与刀具振动速度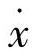的方向相反，这时切削力起一种阻力的作用，因此系统是稳定的，即不会发生自激振动。

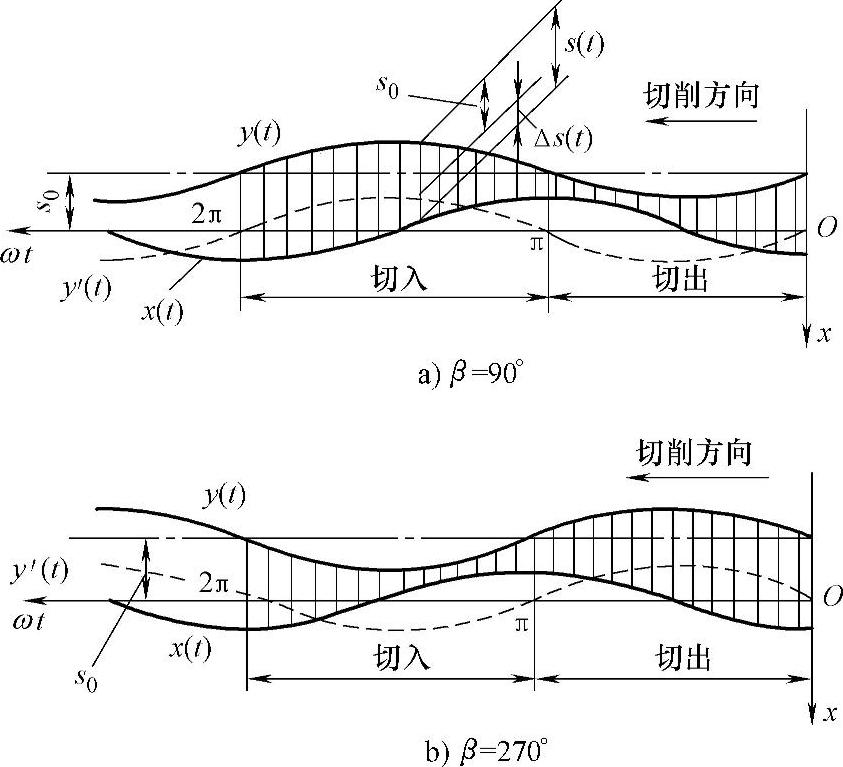
图3-19 正阻尼与负阻尼的发生机理

如果将同样的分析应用于图3-19b中β=270°的情况，则得到图3-20b的结果。这时，动态切削力ΔF基本上与刀具振动速度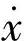的方向相同，对于机床结构的振动来说，此时切削力是“助力”，而不是“阻力”，它助长已经发生的振动，使之不断扩大，因此系统是不稳定的。

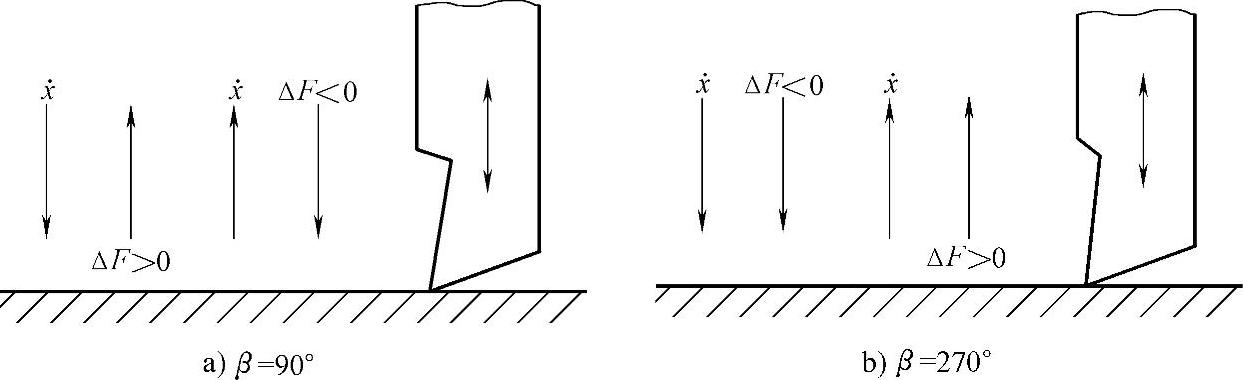
图3-20正阻尼与负阻尼的物理意义

3.3.3.5 能源传输机理

下面计算在一个振动周期中切削力对于振动系统所做的功A：

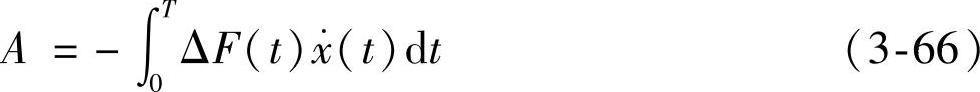
式中的负号是由于F（t）与x（t）的正向不同所致，如图3-15所示。将式（3-55）、式（3-52）和式（3-53）代入上式并积分得

A=-πa²₀a_wk_ssinβ （3-67）

由式（3-67）可见，当β=0°～180°时，A＜0，即切削力对振动系统做负功，振动系统将机械能馈送回切削过程，作为热能消耗掉，因此切削过程是稳定的；当β=180°～360°时，A＞0，切削力做正功，如果此正功大于机床结构的阻尼所消耗的能量，振动能量将不断积累，振动加剧，切削过程是不稳定的。此结论与前面由等效阻尼导出的结论是一致的。

其实，从图3-19也可直观地看出以上结果。首先记住，刀具切出时，切削力做正功，这是因为切削力F（t）的方向总是要将刀具推离工件；而在刀具切入时，切削力做负功。现在看图3-19a，切出阶段的切削厚度一般比切入阶段的切削厚度小，因而切出时切削力所做的正功就比较小，而切入时切削力所做的负功比较大（指其绝对数量），正负相消，切削力做了净负功。而对图3-19b中β=270°的图形作同样的分析，可知切削力做了净正功。此结论验证了式（3-67）的一般规律。