位移反馈、负刚度与静态不稳定性探究

上一节讲述了速度反馈引起的负阻尼及动态失稳现象，现在考虑振动位移的反馈及其效果。设系统的框图如图3-7所示，运动方程为

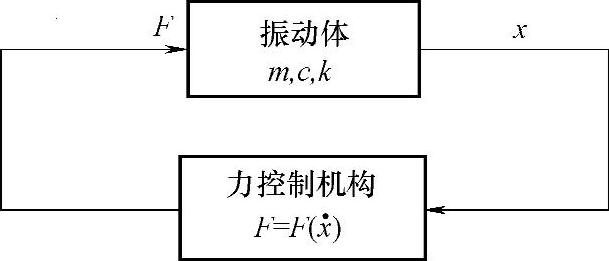
图3-7 位移反馈系统框图

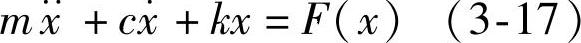
可以看出，此系统的特点是作用在振动体上的力本身又受到其振动位移的控制。式（3-17）中F（x）是一般非线性函数，当x较小时，可将其在x=0附近展成幂级数，仅取其一次项，而略去高次项和常数项，得

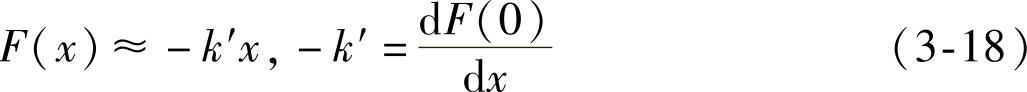
代入式（3-17）并移项，得

式（3-19）从形式上看是一个单自由度系统自由振动的运动方程，但不同的是，其刚度系数由两部分组成：第一部分（k）即为振动物体的刚度，一般是正的；而第二部分（k′）则是由于位移反馈而产生的“等效刚度”，其正负需视函数F（x）的性质而定。如果在x=0附近，函数F（x）随x的增加而降低，即-k′＜0，系统的总刚度（k+k′）＞0，则式（3-19）与单自由度系统的自由振动的运动方程没有什么本质上的差别，仅仅是刚度由于位移反馈而有所增加，相应地系统的固有频率ω₀亦有所提高，则

式中，ω_n是计入“等效刚度”以后的系统固有频率。

如果函数F（x）随x的增加而增加，即-k′＞0，且-k′＞k，则系统的总刚度（k+k′）＜0，即系统的总刚度成为“负刚度”，成为一种不稳定因素。

图3-8分别给出了具有正刚度和负刚度的系统的两个例子，即正摆与倒摆。显然，后者是不稳定的。但是这种不稳定性与上一节讲述的由于负阻尼引起的不稳定性有很大的不同。现回到式（3-20），系统的固有频率为

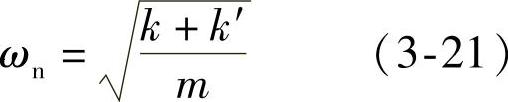
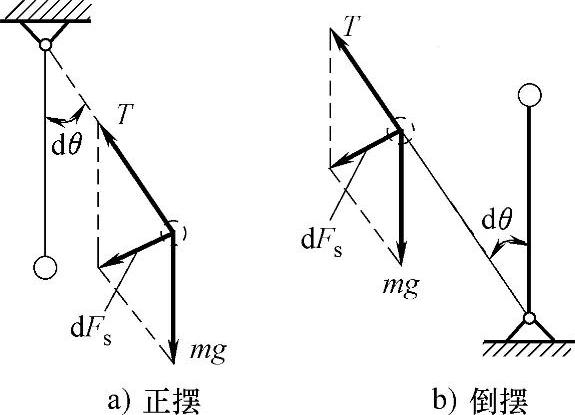
图3-8 正摆与倒摆

在负刚度的情况下，ω_n称为虚数，即系统的固有频率并不存在，这表明系统不可能做图3-8a那样的往复振动，而是以一种位移单调增加的方式偏离其平衡位置。事实上，在式（3-21）中，如果k+k′＜0，即负刚度的情况下引入以下符号

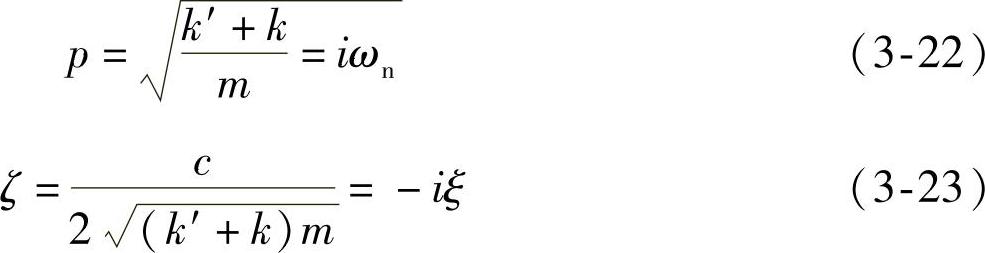
如此定义的p、ζ均为正实数，采用以上符号可将式（3-19）写成

令x（t）=Ae^st

代入上式，即得特征方程

由上式可解出

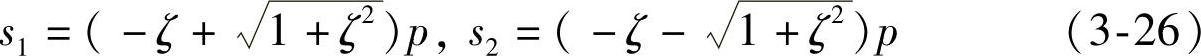
而式（3-24）的通解为

注意到s₁＞0，而s₂＜0，故式（3-27）中第一项会单调增加，而第二项则单调下降趋近于零，如图3-9所示。总的趋势是当时间充分大时，x（t）会单调增加（但是如果A₂较大或s₁较小，那么在t较小的阶段，x（t）可能先下降，然后再上升）。

由负刚度引起的失稳现象称为静态不稳定，以区别于上一节讲的由负阻尼引起的失稳现象（称为动态不稳定）。

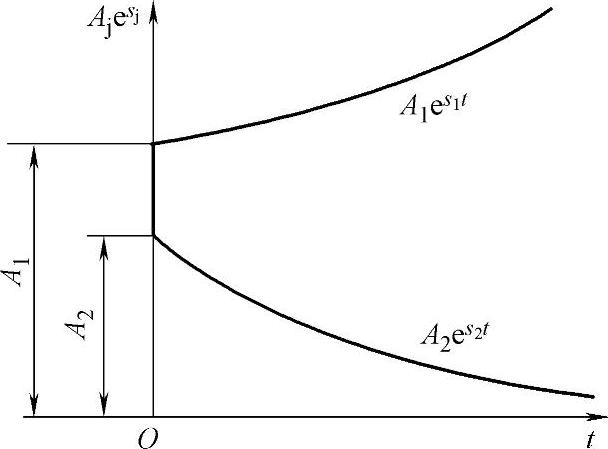
图3-9 式（3-27）右边两项的变化规律(www.xing528.com)

作为静态不稳定的一个实例，现分析金属切削过程中由于刀具变形引起的负刚度及静态失稳现象。图3-10表示经过简化了的切削过程。工件以速度V向下运动，厚度为s₀的一层金属被切削刃切下。向下的切削力为F₀，在其作用下，刀具会发生弹性变形，而切削刃由其不切削时的原始位置O点移到O′点。此时刀具的弹性恢复力F_s（图上未示出）与切削力F₀相平衡。但是必须注意，这种平衡是不稳定的：在切削过程中如因任何偶然的干扰，例如切削刃碰到工件材料中的某一个硬质点，那么切削力F₀会获得一个增量dF，在dF作用下，切削刃再沿OO′O″曲线下移至O″点，此时切削刃下降了dx，而向左伸出ds，后者使瞬时切削厚度增加一个同样的数量，而切削厚度的增加又再度引起切削力的上升，更加促使切削刃下移，刀尖则更深地扎入工件……由此导致刀尖部分会由于迅速上升的切削载荷而崩刃，这种现象称为“扎刀”。此系统的框图可以用图3-11来表示，其中上面一个方框表示刀具（或机床结构），其输入是作用在刀具上的切削力的变动量dF，而输出dx则是切削刃在纵向的变形量；下面一个方框表示切削力的控制机构（即切削过程），其输入是dx，即刀尖在铅垂方向上的移动量，而输出是切削力的变化dF，后者被反馈回刀具上，显然，这是一个具有位移反馈的系统。

近似地将刀具视为一悬臂梁，并认为刀具的装夹是完全刚性的，则由材料力学可知刀具的刚度为

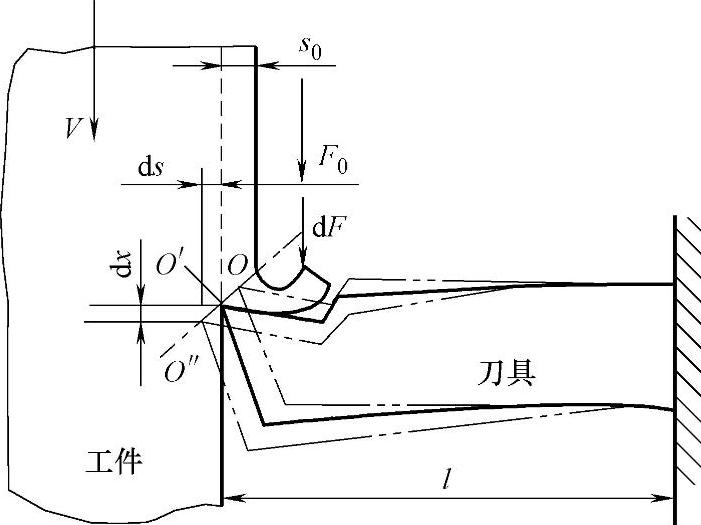
图3-10 静态不稳定实例

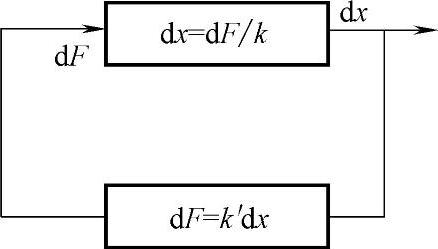
图3-11 静态不稳定实例系统框图

式中，l为刀具的悬伸长度；EI为其抗弯刚度，此刚度是正刚度。

由位移反馈所产生的等效刚度系数k′可推算如下：首先求出图3-12中切削刃的纵向下沉量dx与其横向伸出量ds（即切削厚度的增量）之间的关系。视刀杆为一悬臂梁，在其端部作用有集中载荷dF，则其端部的挠度与转角分别为f=l³dF/（3EI），θ=l²dF/（2EI）。设切削刃到刀杆的中性面之间的距离为Z，则由图3-12中的几何关系，可求得

ds=（3Z/2l）dx （3-29）

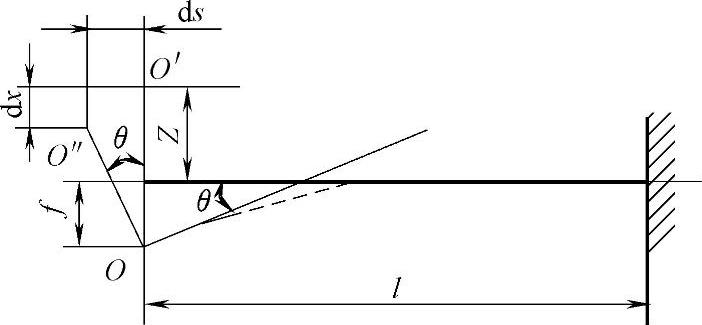
图3-12 刀杆变形与切削刃位移分析

另一方面，将切削力与切削厚度之间的函数关系F（s₀+ds）在s₀附近展成幂级数为

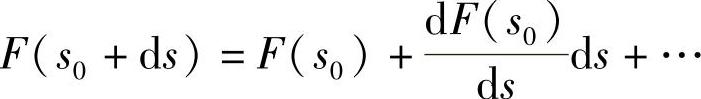
而切削力的增量为

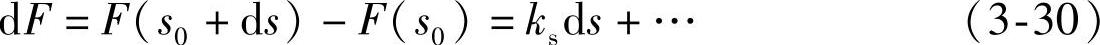
式中

由于F（s₀+ds）是ds的增函数，故应有k_s＞0。将式（3-29）代入式（3-30），得

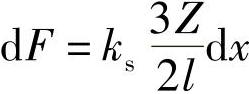
由此得等效刚度系数

由式（3-28），系统总的刚度为

其中，-k_s3Z/（2l）这一部分是由于位移反馈所造成的等效负刚度。产生“扎刀”现象的条件为

防止扎刀的一个有效措施是改变刀杆的形状，使得当切削刃向下变形时，它同时会退离工件，而不是扎入工件，这样式（3-34）中的第二项会变成正刚度，当然不会再有失稳之虞。图3-13所示的弹性刀杆就可以满足以上要求，这种刀具的切削刃在切削力的作用下大体上沿一个圆弧移动，它在向下移动的同时，也向后退。

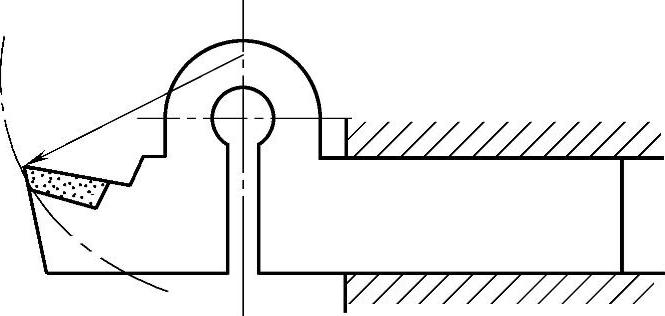
图3-13 弹性刀杆（防止扎刀）

由以上分析可以看到，单纯的位移反馈或者只能使系统原来的正刚度增加，或者形成负刚度而引起静态不稳定，但不可能引起动态不稳定，即不可能引起自激振动。以下我们会看到，位移的延时反馈却可以引起自激振动。