能量平衡与振幅稳定性分析

以下从能量平衡关系来讨论系统的振幅稳定性与稳定振幅。由式（3-12）可得到系统的阻尼在一个振动周期中消耗的能量-W_d与振幅A之间的关系，如图3-6中粗实线所示；式（3-11）所表示的切削力所做正功W_p在图3-6中用点画线表示。就图中所示的情况而言，由于在任何振幅A下，均有-W_d＞W_p，因而在这种情况下不可能发生颤振。以上曲线W_p是按c′的一定的值绘出的，设想∣c′∣取另一更大的数值，可得到另一曲线W′_p，如图3-6中虚线所示。这时由于在任一振幅A下，总有W′_p＞-W_d，因而将发生自激振动，振幅将不断扩大。

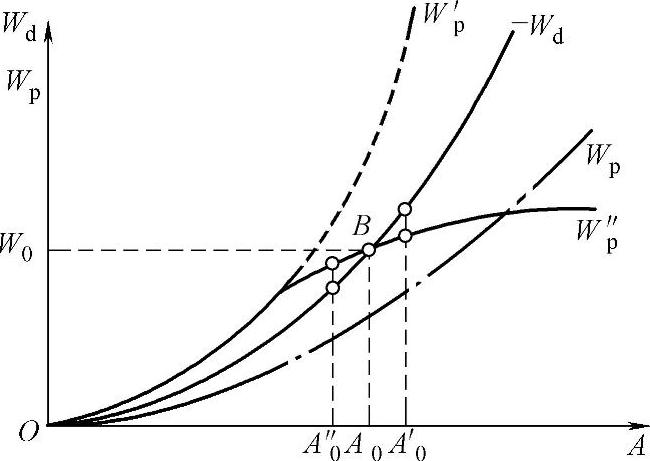
图3-6 能量平衡与振幅稳定性

图3-6中诸曲线均为抛物线，它们除了在原点相切以外，再无别的交点，即能量的积聚与能量的耗散总是无法平衡，要么如曲线-W_d与W_p所示，并不能产生自激振动；要么如曲线-W_d与W′_p所示，振幅将无限上升。总之，是一种无法实现稳定的自激振动。但事实上，自激振动系统一般都具有振幅稳定性。为了解释这一问题，需将式（3-2）表示的切削力中的高次项＜即非线性项＞纳入考虑。为此，将式（3-2）代入式（3-10），得

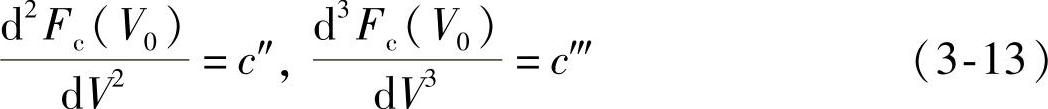
且略去大于三次的项与常数项F_c（V₀），得切削力在一个振动周期中所做的正功为

再将式（3-9）代入，并积分得(www.xing528.com)

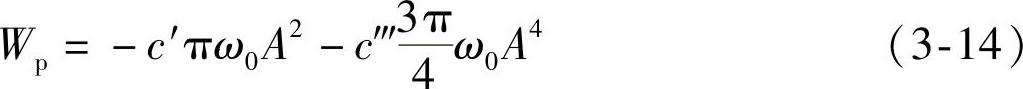
在达到能量平衡时，应该有W_d+W_p=0，将式（3-12）与式（3-14）代入这一条件，有

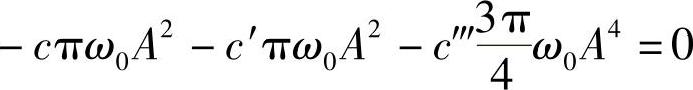
由此可解出达到能量平衡时的稳定振幅为

前面说过，发生自激振动的条件是c+c′＜0，而由上式，为了得到稳定振幅的实数解，应有c‴＞0。再看式（3-14），其右边第一项取正值，其值随A²而上升；而第二项取负值（因为c‴＞0），这是一种抑制W_p上升的因素。当振幅A较小时，此因素并不显著，可是当A上升时，这一抑制作用会急剧地上升。在图3-6中，曲线W″_p（细实线）是将后面这一项非线性因素纳入考虑以后的W_p与A的关系曲线。将之与曲线W′_p（虚线）比较，可以明显地看出非线性项的抑制作用。W″_p与-W_d两条曲线的交点B即给出系统的稳定振幅A₀。为了说明此振幅A₀是稳定的，假设由于偶然因素的干扰，振幅由A₀突然增加到A′₀，这时从图上可见有-W_d＞W″_p，即能量的消耗大于能量的积聚，系统的总能量下降，因而振幅下降，由A′₀降回至A₀点；反之，若由于偶然干扰，A₀下降至A″₀，由类似的分析也可看出系统的总能量将会上升，而使振幅由A″₀回升至A₀。