探讨自激振动的能量机理

现分析自激振动系统的能量输入与能量消耗机理。

3.2.3.1 切削过程的能量机理

当机床工作在切削力的下降特性区域时，切削力将对振动系统做净正功，即对振动系统输入能量；而当机床工作在切削力的上升特性区域时，切削力对振动系统做净负功，即振动系统的能量被切削过程耗散掉。为了说明这一问题，试比较图3-4c与图3-4d，它们分别表示在上述两种条件下，刀具在x方向（铅垂方向）的振动位移与其所受切削力之间的回线关系。先看图3-4c，在x增加的半个周期中，F_c与x的关系如曲线abc所示，而在x减小的半个周期中，F_c与x的关系如曲线cda所示。这两者的差别是由于速度的不同而引起的：在前半个周期中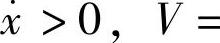，比较大，因而切削力F_c比较小；而在后半周期中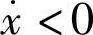，，比较小，因而切削力比较大，由此F_c-x的关系分成两支，而成为回线。由于切削力的方向总是指向x的负向（图3-4a），因而在前半周期中切削力做负功，负功的数量由图形abcfOea的面积给出；而在后半周期中切削力做正功，正功由图形cdaeOfc的面积给出。显然，在数量上正功大于负功，而闭曲线abcda的面积给出了在一个振动周期中，切削力所做的净正功，即输入振动系统的能量。对图3-4d进行同样的分析，可见闭曲线ad-cba给出了一个周期中切削力所做的净负功，即耗散掉的振动系统的能量。

为了从数量上估算通过切削过程所输入或所耗散掉的振动能量，假定阻尼率ξ很小，因而式（3-8）中的，ω_d≈ω₀，且通过适当选择时间起点，可使初相ϕ=0，于是式（3-8）简化为

切削力在一个振动周期中所做的功为

把式（3-4）、式（3-9）代入式（3-10）得

积分后，得(www.xing528.com)

显然，当工作在切削力的下降特性区域时，由式（3-3）有c′＜0，因而W_p＞0，即切削过程做正功，对系统输入能量；反之，当工作在切削力的上升特性区域时，c′＞0，W_p＜0，切削过程做负功，振动能量通过切削过程而耗散。

3.2.3.2 机床结构的内阻所耗散的能量

一个振动周期中机床结构的内阻所耗散的振动能量为

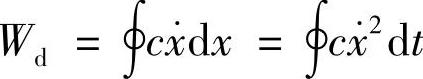
将式（3-9）代入，并积分，得

由于恒有c＞0，故W_d＜0，表明机床结构的阻尼力只会对振动系统做负功，使振动能量耗散。当W_p+W_d＞0时，切削力的下降特性就可能使切削过程失稳，引起颤振。