速度反馈对负阻尼的影响

将式（3-1）右边的在V₀附近展开，得

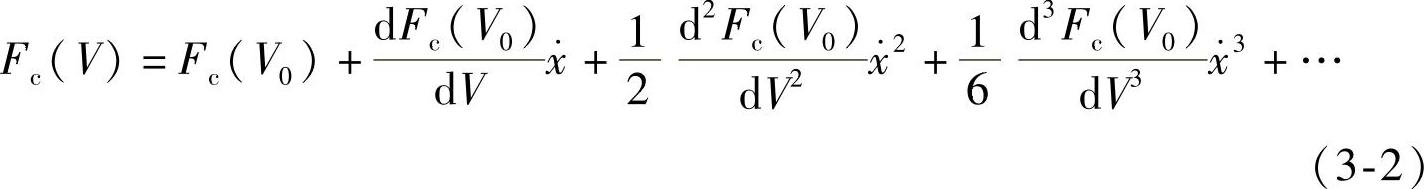
如果仅研究刚开始发生颤振的情况，可以假定与V₀比较起来，很小，因而可仅取其线性项，而略去高次项。又由于上式中的恒量F_c（V₀）对振动并无影响，可以略去，即

可将式（3-2）简化为

代入式（3-1）并移项，得

这是一单自由度系统自由振动的运动方程，它与普通的振动系统不同，其系统的阻尼由两部分组成：一部分是振动系统（机床结构）本身的阻尼，这是通常意义下的阻尼，即对于振动的一种阻碍，其阻尼系数c取正值，这种阻尼称为“正阻尼”；另一部分是由于速度反馈而形成的等效阻尼，其阻尼系数c′可以为正，也可以为负，需视V₀在V-F_c曲线上的位置而定。如果V₀处于切削力的上升特性部分，如图3-4b中B点，则由式（3-3）可知c′=dF_c（V₀）/dV＞0，从而总的阻尼c+c′＞0，即为正阻尼；如果V₀处于切削力的下降特性部分，如图3-4b中A点，则c′=dF_c（V₀）/dV＜0，这时等效阻尼是一种“负阻尼”。当这种负阻尼足够大，胜过系统本身的正阻尼时，总的阻尼就可以变成负的，即c+c′＜0。前面说过，负阻尼实际上是一种“助力”，它不仅不会阻碍系统的振动，反而会推波助澜地扩大系统的振动。令

(www.xing528.com)

式（3-5）成为

式中，ξ为总的阻尼率，它可以为正、为零或为负。上式的通解为

式中，，对应于ξ＞0、ξ=0与ξ＜0三种情况下的振动历程，分别如图3-5所示。这三种情况下的系统分别称为稳定的、临界的与不稳定的。

图3-5 不同阻尼率下的振动历程

一个具有负阻尼的系统之所以是不稳定的，是由于它处在一种“一触即发”的状态下，只要有任何一个扰动激起，哪怕是非常微小的初始振动（位移或速度），也会由于负阻尼之助而不断扩大，发展成为强烈的自激振动。这类自激振动称为由切削力的下降特性引起的颤振。