相平面、平衡点、极限环及其稳定性探究

1.相平面

自激振动可以直观地在相空间里加以表述。对于单自由度系统来说，相空间是由振动位移x=x₁及振动速度x=x₂这两个坐标所形成的相平面，如图3-1所示。相平面上的每一点称为一个“状态点”。每一个状态点代表一定的振动位移和一定的速度的组合。当系统振动时，其位移与速度均在连续变化，而状态点则在相平面上画出一条曲线，称为轨线；轨线的全体形成相图。相图反映了一个振动系统的整体动态特性。

相图上的平衡点和极限环分别对应于一个振动系统的定态和周期运动，这两者往往在工程上具有实际意义，值得认真研究。

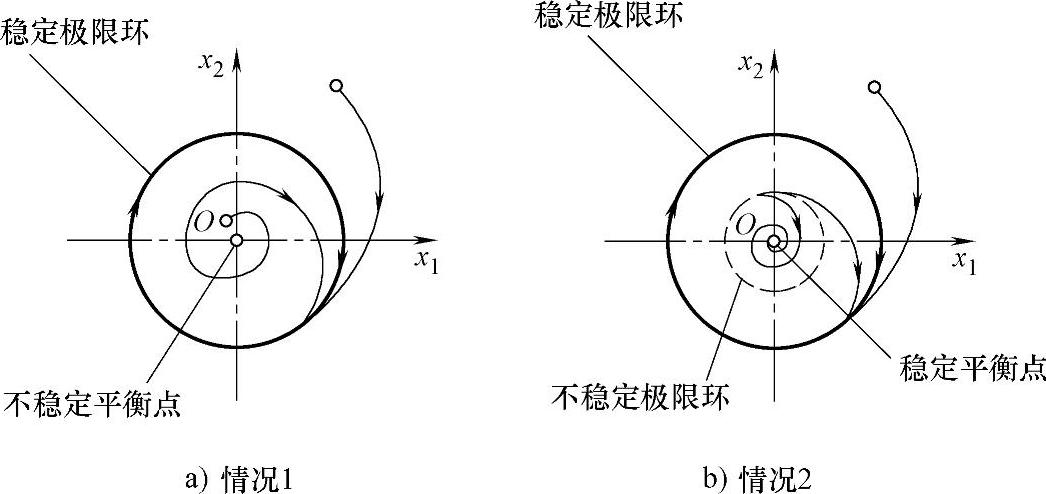
图3-1 相平面、相图、平衡点和极限环

2.平衡点及其稳定性

当一个动态系统处于平衡状态时，其速度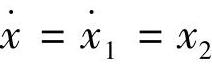（）与加速度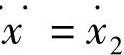（）均为零，即有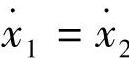=0。相平面上满足这一条件的点称为平衡点。例如，图3-1中假定原点为平衡点。显然，一个处在平衡点上的系统由于既无初速度，又不受力（加速度为零），当然不会自行运动起来。

平衡点分为两类，即稳定平衡点和不稳定平衡点。其差别并不在于平衡点本身的状态，而在于系统略为偏离其平衡点时的运动趋势：是趋向于回到平衡点、保持在平衡点近旁运动或者趋向于偏离该平衡点越来越远。相应地，该平衡点的运动趋势称为渐近稳定的、仅稳定的或不稳定的。

必须了解“平衡”与“稳定”这两个概念之间的联系与差别。须知，“平衡点”并不一定稳定，而“稳定性”则一定是围绕某一平衡点而言的。这些概念对于理解一个金属切削系统的稳定性是至关重要的。一般说来，一个金属切削系统如果能够稳定地运行，则它应该工作在其平衡点上。但这还不够，应该说，它必须工作在其稳定平衡点上。这是由于，一个真实的金属切削系统必然经受各种各样的扰动，只有稳定平衡点才具有抗扰动的能力，从而能将金属切削系统维系在其周围，稳定地运转。对于处在这种平衡状态下的金属切削系统，任何短暂、微小的扰动只会引起其工作状态短暂、微小的变化，而这些变化一般是工程实践可以容忍的。稳定平衡点对应于金属切削系统的定态解。可是，对于不稳定平衡点来说，任何短暂、微小的扰动，都会使金属切削系统永远地、大幅度地偏离其正常工作点，完全破坏金属切削系统的工作条件。由于这种不稳定平衡状态不具备抗扰动的能力，而现实世界又总是充满着各种各样的扰动；因此，所谓不稳定平衡状态只是一种理论上的平衡状态，实际上是观察不到的。

不稳定平衡点是一种中间状态，它对应于一种稳定的振动，在研究机床颤振时，我们仍然将它视为一种不稳定的状态。(www.xing528.com)

3.极限环及其稳定性

我们知道^[123]，保守系统由于机械能守恒的缘故，其振动轨线是一条封闭的曲线。机床振动系统由于与外界存在能量交换，因而属于非保守系统。非保守系统的相图中也可以存在一种封闭的轨线，如图3-1a和图3-1b中的粗实线和虚线圆圈所示。与保守系统不同，这类非保守系统的封闭轨线具有以下特点。

1）非保守系统在一封闭轨线上运动时，其总机械能并不守恒，它既吸收能量，又耗散能量，总机械能在不断变化。只不过经过一周以后，能量的“收支”必须平衡，而系统的状态变量返回原状，然后再开始下一个周期的运动。

2）非保守系统的封闭轨线还可以具有一种“吸引力”，它可以把从该轨线以外的其他点上出发的轨线“吸引”到该封闭轨线上来。如图3-1中以粗实线表示的封闭轨线即具有这种性质。因此，非保守系统的这种封闭轨线代表一种与初始条件无关的周期运动。这种周期运动是由系统本身决定的，初始条件的变化（图3-1a），或者初始条件在一定范围内变化（图3-1b），并不影响系统最后趋近的这种周期运动。而众所周知，保守系统的封闭轨线是由其初始条件决定的，而且相平面上对应于不同初始条件的封闭轨线并不相交。

具有以上特性的非保守系统的封闭轨线称为“极限环”（Limited Cy-cle）。极限环对应于系统运动的周期解。除了定态解（平衡点）以外，周期解（极限环）也是动态系统的一种重要的运动方式。因此，对极限环的研究具有实际的工程意义。

极限环分为稳定的与不稳定的两种。前述图3-1a、图3-1b中以粗实线表示的极限环是稳定的，而图3-1b中以虚线表示的极限环则是不稳定的。一般而言，对于一封闭轨线c，如果其附近的任一轨线都始终保持在它附近，则称c是轨道稳定的；如果其附近的轨线当时间t→∞时都无限趋近于c，则称c是轨道渐近稳定的；如果其附近的轨线都倾向于离开c越来越远，则称c是轨道不稳定的。

稳定极限环具有轨道稳定性，即具有抗扰动的能力。当系统沿某一稳定极限环运动时，即使由于外界扰动使它暂时地偏离该极限环，但它终归还是会回到该环上，或者保持在该环附近运动，不至于产生过大偏差。而不稳定极限环只是理论上的一种可能性，由于实际环境中的各种扰动不可避免，因此在实践中是不可能观察到沿着不稳定极限环运动的。

图3-1给出了极限环与平衡点的两种典型的配置方式。图3-1a中，原点是不稳定的平衡点，而包围原点的极限环是稳定的；图3-1b中，原点是一个稳定平衡点，其外包围着一个不稳定极限环（虚线），再外层是一稳定极限环（实线）。在图3-1b的情况下的原点，对于小的扰动（在虚线环之内）是稳定的，而对于大的扰动（超过虚线环）则是不稳定的。这种原点称为具有“有限振幅不稳定性”。

平衡点与极限环相结合，可以用来描述自激振动的过程与特点。在图3-1a的情况下，系统不可能静止在其中心的平衡点上，任何微小的初始扰动均会激起不断上升的振动，而最后振动被约束在稳定极限环上。在图3-1b的情况下，如果扰动不越出虚线环所规定的阈限，系统可以稳定在其中心平衡点上；一旦扰动越过这一阈限，就立即激起增幅的自激振动，而最后振动被稳定在外层的实线（稳定）极限环上。