【摘要】：MMC修正时的零位置度公差不适合应用在过渡配合或过盈配合中。MMC或LMC修正时的几何公差的零公差很容易判断是否合适。如对于一个同轴的零件需要旋转的时候，通常不会使用MMC或LMC控制，因为当特征偏离MMC时，零件的质量分布必然不均匀。并且由于自对中性，在螺纹孔或锥形沉孔的情况下也不适用零位置度公差。
MMC修正时的零位置度公差不适合应用在过渡配合或过盈配合中。对于浮动零件（如销或轴），没有自己的位置度公差，其相对的匹配特征对于定位基准的位置度控制也不会太重要。
MMC或LMC修正时的几何公差的零公差很容易判断是否合适。如对于一个同轴的零件需要旋转的时候，通常不会使用MMC或LMC控制，因为当特征偏离MMC时，零件的质量分布必然不均匀。并且由于自对中性，在螺纹孔或锥形沉孔的情况下也不适用零位置度公差。并且这些情况中的公差补偿量计算很复杂。
然而，如果设计者关心的是匹配特征能够在总成中装配到一起，当尺寸定义和基准指定适当时，零位置度公差是最好的定义方式，能够将零件的合格率提高到最多。这意味着，在零件的验证过程中，更注重零件的功能（装配功能），而不是单单的尺寸约束。
(www.xing528.com)
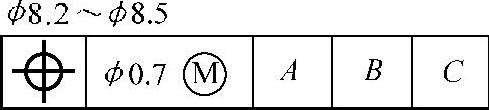
图7-30 轴的位置度定义
下面讨论图7-30所示轴的位置度定义。
如果只考虑这个轴的装配（相对于基准的定向和定位控制），这个轴和一个定位轴的同样的基准框架定位的孔配合。这个定义会导致许多能够满足装配的零件被拒收。这个零件的最差匹配条件（实效边界）是MMC加上受控特征在MMC时的几何公差，为φ9.2mm（8.5+0.7=9.2）。所以这个孔理论上能够接收那些实效边界小于或等于φ9.2mm的所有轴。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
