几何公差与尺寸公差的比较

1.公差带的比较

首先我们从这个经典的例子说起，图1-3所示为一个孔板尺寸公差的标注和这个尺寸公差控制的正方形公差带。

图1-3 尺寸公差约束的公差带

通常情况下尺寸公差带是正方形的。在一些特殊的要求下（如保证某一方向上的壁厚或特定的功能），尺寸公差带也可能是矩形的。

在实际装配中，孔和轴的配合间隙在360°方向上都应该是相等的。这就意味着配合轴的浮动范围（轴的轴线的位置公差带）应该是一个圆柱面。所以实际装配情况的公差带与尺寸公差定义的矩形公差带是不相符合的。

正方形的公差带没有反映出孔的实际装配条件。轴的轴线在矩形的公差带内浮动，在360°方向上距离理论的装配中心是不等的。当轴线处于正方形的对角线位置上，距离理论装配中心最远，导致的装配间隙最小。当轴线处于正方形的4个正交方向上配合间隙最大。所以为了保证装配间隙或避免干涉，设计者应该以这个矩形公差带的对角线的距离来计算。但是通常的做法都是以正交方向上的浮动距离来计算的，这就导致了产品在最终成品上会出现干涉的风险。

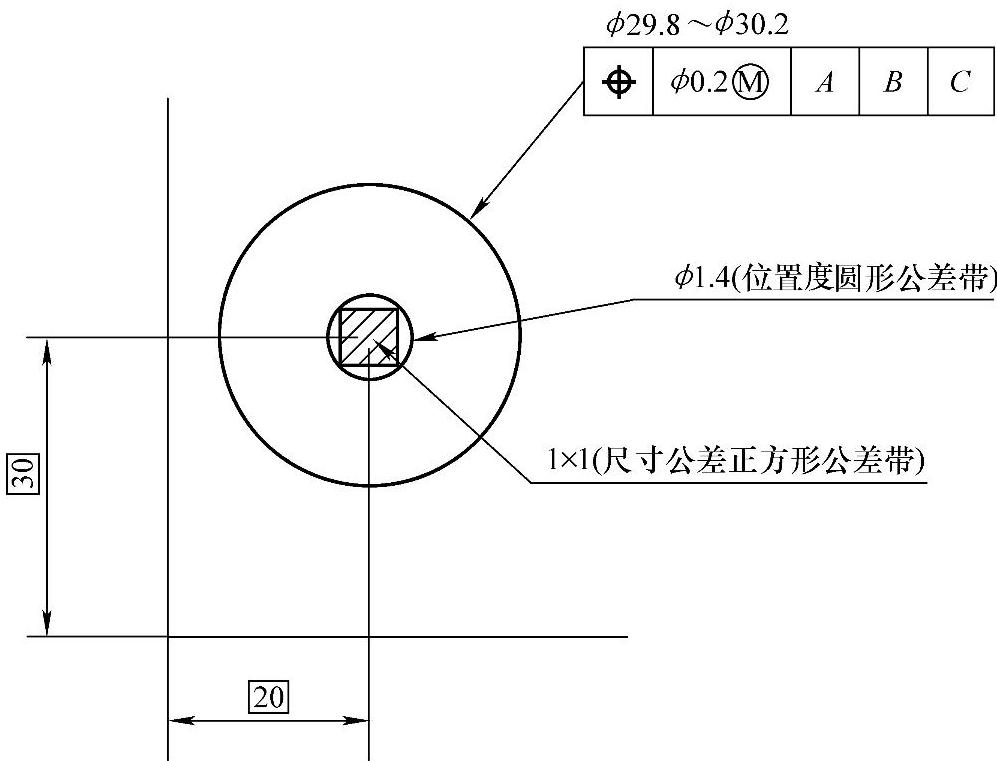
图1-4 几何公差（位置度）约束的等效公差带

可以判断出，这个实际配合的圆柱面公差带外切于尺寸公差的正方形柱面。即如果正方形的公差带能够满足配合，那么以这个正方形对角线为直径的圆柱也能满足装配。对于这个装配的圆柱面公差带，可以按图1-4进行等效GD＆amp;T设计，这个位置度公差控制方式描述了一个圆柱面公差带φ1.4mm，为正方形公差带的对角线长度。

如果实际零件尺寸落在圆和正方形不相交的区域，就意味着合格的零件被当作不合格的零件拒收。这一部分的面积是尺寸公差带不可避免产生的，造成了浪费，同样地，也因为公差控制更严，加工成本也会增加。

两种公差带的面积计算比较如下：

正方形的尺寸公差带面积

S₁=1×1mm²=1mm²

圆形的几何公差带面积

两种公差标注的面积差

S₀=S₂-S₁=（1.57-1）mm²=0.57mm²

几何公差比尺寸公差带多出的面积比

S₀/S₁=57%

几何公差的公差带比尺寸公差的面积区域大出57%（见计算式），并且，如果应用最大实体原则，意味着当尺寸由最大实体尺寸增大到最小实体尺寸时，这个值还可以随着扩大，这就是几何公差中的公差补偿。更大的公差意味着更具经济性。但是我们不应该判断至少57%的零件被浪费掉了，因为稳定生产的零件尺寸遵循不相关随机分布，是一个正态分布曲线，尺寸集中在中值附近，需要知道相关的标准差才能计算出不合格的零件数量。

对于这个装配孔，要满足装配功能，需要一个位置公差。我们观察一下，尺寸公差定位这个孔的公差带是一个正方形，如图1-3所示。如果不考虑壁厚影响和其他特殊要求，在此例中几何公差规定的公差带应该是一个圆形。就是这个孔和轴的装配在任何方向上应该是等间隙的，如图1-4所示。假设一个螺栓穿过此孔，合理的理解是围绕螺栓在任何方向上间隙（即设计公差带）的分布是均匀的（圆形的公差带）。但是很明显，尺寸公差的公差带的分布是不均匀的，对角线方向上的变化最大，这就导致了正方形公差带必须内切于圆形公差带，牺牲了空白区域内的公差带，尺寸公差无法描述这一合理公差带区域。位于这个区域内的公差（实际能够满足装配）被作为不合格的零件检出。看一下这部分的面积比，达到57%！从这个例子可以看出，尺寸公差带人为地缩小了公差带的大小。这就意味着，合格的零件以废品的形式被检出，造成浪费！而缩小公差带，则增加了加工成本！而且我们在本书后面会介绍，几何公差控制的公差带不是固定的，可以应用公差补偿的理念，在公差要求的范围内扩大公差带，以降低成本；而尺寸公差是一个固定的公差带，无法优化，给公差分配带来困难，成本相对较高。(www.xing528.com)

尺寸公差的矩形公差带无法适应复杂的装配。比如异型孔，如销孔特征的公差带是何种形状呢？一些工程图的标注习惯将长圆孔的位置度描述成圆形，或者为尺寸公差的矩形，我们要注意这种标注方式会造成最终无法装配的风险！对于公差带的理解直接关系检测销的形状设计。我们在讲述位置度的时候会详细解答这个问题。

几何公差的公差带可以按照实际的装配需要去定义，也容易验证，能够实现检具检验。

2.基准的问题

尺寸公差往往需要假设测量基准点，造成两个配合零件即使都按照图样制作，也可能造成实际不能够装配在一起，如图1-5所示。

图1-5 尺寸公差的基准不确定性

对于任何实际加工零件，如图1-5中的孔板，在微观状态下会产生这种平行四边形的情况。这个零件如果在设计时以底边定位，设计者无法使用尺寸公差语言来表达这个要求。若加工者或其他的供应商无法直接和设计者沟通，则会按照设备的情况进行工艺定位加工中间的孔，如图1-5b所示。这种假设按照尺寸公差图样理解没有错误。检测者可能也假设出一个测量基准来测量中间的孔，如图1-5c所示。从这个流程可以看出，尺寸公差存在合理假设，描述逻辑不严密造成了最终检测可能合格，但是无法完成装配的情况。基准的不确定造成了项目的风险。

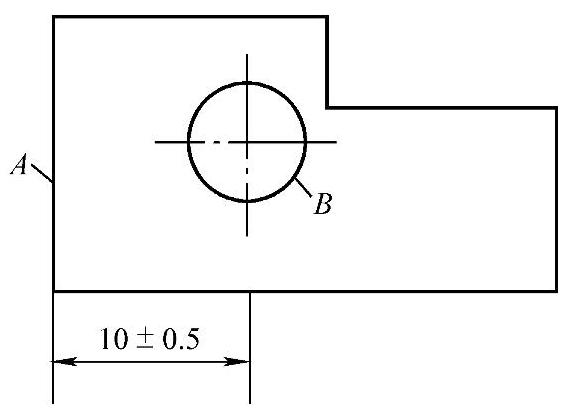
图1-6 尺寸公差的工艺不确定性

（不能确定是孔定位边，还是边定位孔）

图1-6存在两种合理的解释：①先加工孔B，然后由孔B定位加工边A；②先加工边A，然后由边A定位加工孔B。这两种工艺方式实际上在一定精度要求下会造成明显的变差。类似存在假设的尺寸公差标注的还有很多。假设就意味着多种可能，处于假设状态的设置也会因人不同。对于复杂的零件，这种基准不明的情况会导致不同的公差积累结果。图1-5和图1-6所示的标注不能明确加工的工艺和测量的基准。

另外，尺寸公差不能体现实际测量、加工或工装检具设计时基准选择的顺序性。几何公差有完善的基准定义。这个优点虽然是几何公差的核心内容，但不是被很多人了解。基准的设置不同会产生不同的加工结果，这在尺寸公差中也会体现。一个复杂的零件，对于一个有经验的工程师，他会将所有的尺寸尽量设置在一个基准点上，也就是说所有的测量起始于相同的一点，但不能解决所有的基准定位问题。

总之，尺寸公差体现不了基准顺序，有时缺少测量的基准点，并很难描述一个复杂的零件。一个零件在空间中有六个自由度，几何公差可以很容易地通过基准约束这些自由度，而尺寸公差没有这方面的功能。

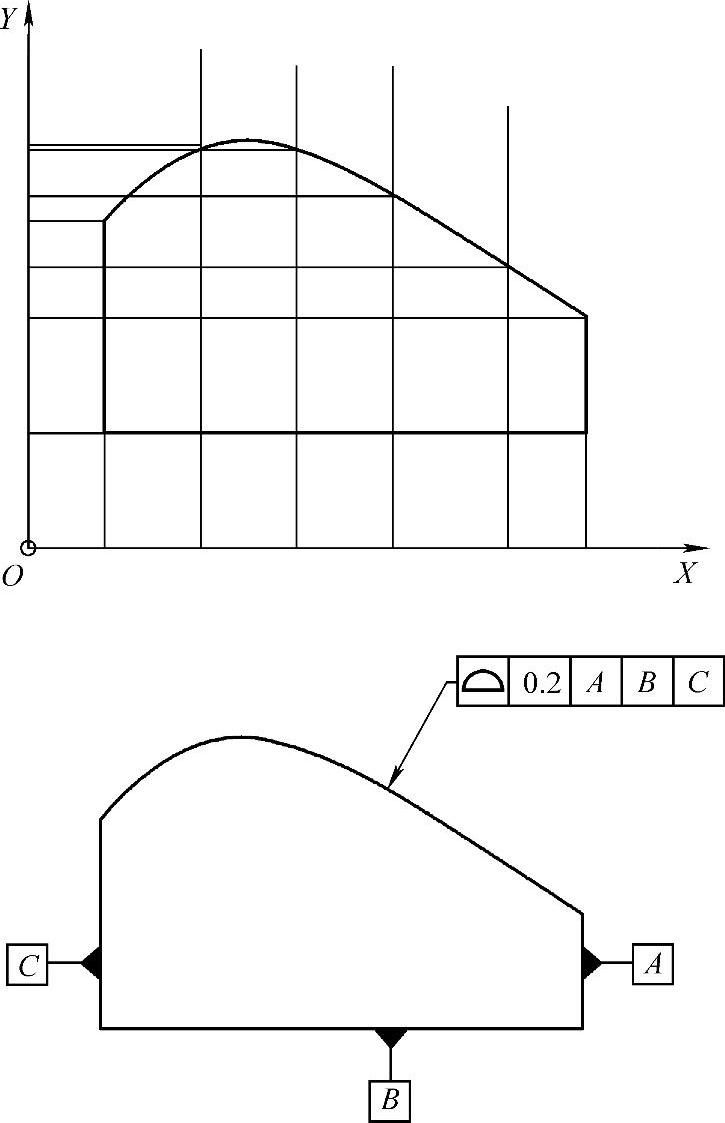
图1-7 尺寸公差和几何公差对于异形特征的定义

3.对于异形特征的描述

通过图1-7可以明显看出，几何公差比尺寸公差表达更简练，能简单准确地传递设计意图。

图1-7所示是对一种零件的两种标注方法。对于这个异形件，尺寸公差方法不仅繁琐而且不能准确表达这个零件准确的曲线轮廓，因为在坐标点之间的曲线轮廓是没有定义的。而几何公差的方法可以连续地描述这个曲线。由于CAD、CNC和CMM技术的发展，加工工艺和检测方法日趋先进，几何公差方法的优势更加明显。

传统的尺寸公差测量方式停留在二维和坐标法验证层面，而CMM是在三维空间验证一个零件，几何公差正是为适应这种先进检测加工设备而产生的。对于几何公差，更快的方式是使用功能检具，只验证合格或不合格两种结果。但这种检具不能收集数据，如数量型测量工具CMM设备。

本书的前部分内容是关于几何公差的基础知识介绍，后部分内容是一些精选的几何公差应用实例。