基于2的FFT算法原理，求解离散数字信号谱

离散傅里叶变换（DFT）是可以用数字方式来实现的从时域到频域的变换，FFT是DFT的一种快速算法，它把N²次运算减少为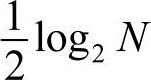次运算。

以基2按频率抽取FFT算法为例介绍FFT原理，对于有限长离散数字信号{x[n]}，0≤n≤N−1，其离散谱{x(k)}可由DFT求得。DFT定义为

离散傅里叶变换（DFT）是可以用数字方式来实现的从时域到频域的变换，FFT是DFT的一种快速算法，它把N²次运算减少为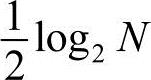次运算。

以基2按频率抽取FFT算法为例介绍FFT原理，对于有限长离散数字信号{x[n]}，0≤n≤N−1，其离散谱{x(k)}可由DFT求得。DFT定义为

式（7-1）可改写成如下形式：

式（7-1）可改写成如下形式：

不难看出，W_N^nk是周期性的，且周期为N，即

不难看出，W_N^nk是周期性的，且周期为N，即

W_N^nk的周期性是DFT的关键性质之一。为了强调起见，常用表达式W_N取代W，以便明确地给出W^nk的周期为N。

对于按频率抽取形式的FFT，输入序列{x[n]}要按下述方式分成两个各有N/2个样本的序列。第—个序列{x1[n]}由{x[n]}的前N/2个点组成，而第二个序列{x2[n]}由{x[n]}的后N/2个点组成。因此

x1[n]＝x[n] n＝0,1,2,…,N/2−1 （7-3）

x2[n]＝x[n+N/2] n＝0,1,2,…,N/2−1 （7-4）

现可将x[n]的N点DFT写成如下形式：(www.xing528.com)

W_N^nk的周期性是DFT的关键性质之一。为了强调起见，常用表达式W_N取代W，以便明确地给出W^nk的周期为N。

对于按频率抽取形式的FFT，输入序列{x[n]}要按下述方式分成两个各有N/2个样本的序列。第—个序列{x1[n]}由{x[n]}的前N/2个点组成，而第二个序列{x2[n]}由{x[n]}的后N/2个点组成。因此

x1[n]＝x[n] n＝0,1,2,…,N/2−1 （7-3）

x2[n]＝x[n+N/2] n＝0,1,2,…,N/2−1 （7-4）

现可将x[n]的N点DFT写成如下形式：

式（7-5）中用了W^Nk/2=e−^jπk这一关系。如果现在分别考虑DFT的偶数样本和奇数样本，则有如下关系：

式（7-5）中用了W^Nk/2=e−^jπk这一关系。如果现在分别考虑DFT的偶数样本和奇数样本，则有如下关系：

式（7-6）和式（7-7）表明，N点DFT转换成了N/2点DFT的问题。

反复运用这一方法，将每个点DFT表示成两个点DFT的组合，最终直接算出两点DFT的简化结果。

式（7-6）和式（7-7）表明，N点DFT转换成了N/2点DFT的问题。

反复运用这一方法，将每个点DFT表示成两个点DFT的组合，最终直接算出两点DFT的简化结果。