时序逻辑电路的基本分析方法

【例7.1】 图7.2所示时序逻辑电路，其输出信号由各触发器的Q端取出。设触发器现态为“0”态，试分析该电路的逻辑功能。

解 （1）判断电路类型。该时序逻辑电路除CP时钟脉冲外，无其他输入信号，且各触发器的时钟脉冲不同，因此判断是莫尔型的异步时序逻辑电路。

（2）写出该时序逻辑电路分析时所需的相应方程式。该时序逻辑电路的各位均为CP上升沿到来时发生状态翻转的D触发器，因此电路的驱动方程为

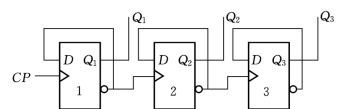
图7.2　[例7.1]逻辑电路

直到第八个CP脉冲上升沿到来时，Q3Q2Q1由111又重新转换为000状态。以后电路将周而复始地重复上述循环。

把以上分析结果填写在状态转换真值表中，见表7.1。

表7.1　[例7.1]逻辑电路状态转换真值表

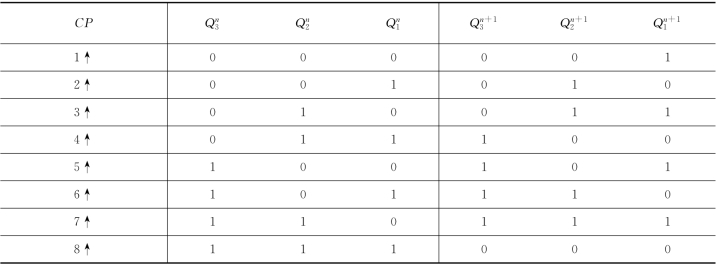
观察上表可看出，电路中的各位触发器状态变化的规律是：每来一个CP脉冲上升沿，触发器1的状态就会翻转一次；每当Q1出现下降沿时，触发器2的状态就会翻转一次；每当Q2出现下降沿时，触发器3的状态将翻转一次。

另外，该时序电路在运行时所经历的状态是周期性的，即在有限个状态中循环，通常将一次循环所包含的状态总数称为时序逻辑电路的 “模”。所以，该时序逻辑电路是一个异步三位二进制模8加计数器电路。

异步三位二进制模8加计数器的状态转换还可用图7.3所示的状态转换图来表示。

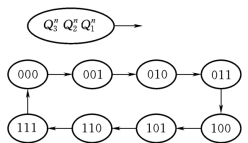
图7.3　[例7.1]电路状态转换图

对 [例7.1]的异步时序逻辑电路进行分析时，首先要看触发器的触发脉冲有无有效的触发边沿或有效的触发电平，只有出现有效触发信号时，才能根据这一时刻的触发器输入信号依据次态方程求出变化后的新状态。

通过[例7.1]可以了解到时序逻辑电路的一般分析步骤通常为：

（1）确定时序逻辑电路的类型。根据电路中各位触发器是否共用一个时钟脉冲CP触发电路，判断电路是同步时序逻辑电路还是异步时序逻辑电路。若电路中各位触发器共用一个时钟脉冲CP触发，为同步时序逻辑电路；若各位触发器的CP脉冲端子不同，如图7.2所示电路，就为异步时序逻辑电路；根据时序逻辑电路除CP端子外是否还有输入信号判断电路是米莱型还是莫尔型，如有其他输入信号端子时，为米莱型时序逻辑电路，如果像[例7.1]所示电路没有其他输入端子，就是莫尔型时序逻辑电路。(https://www.xing528.com)

（2）根据已知时序逻辑电路，分别写出相应的输出方程（注：莫尔型时序逻辑电路没有输出方程）、驱动方程和次态方程，当所分析电路属于异步时序逻辑电路，还需要写出各位触发器的时钟脉冲方程。

（3）根据次态方程、时钟方程、输出方程或时钟脉冲方程，填写出相应状态转换真值表或画出其状态转换图。

（4）根据分析结果和转换真值表（或状态转换图），得出时序逻辑电路的逻辑功能。

【例7.2】 分析图7.4所示时序逻辑电路的功能，说明其用途，设电路的初始状态为“111”。

解 （1）电路中各位触发器时钟脉冲为同一个CP 输入端，具有同时翻转的条件，而且电路中除了三位触发器，还有两个与门，因此判断该电路为米莱型的同步时序逻辑电路。

（2）电路的驱动方程为

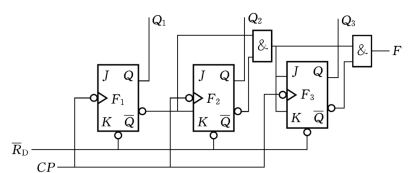
图7.4　[例7.2]逻辑电路

电路的输出方程为

电路的次态方程为

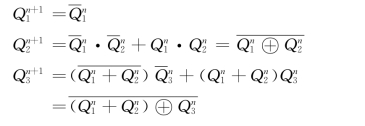
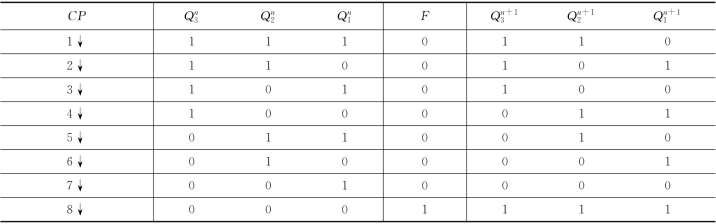
（3）根据上述方程，填写相应真值表见表7.2。

（4）由真值表可看出，此电路为同步二进制模8减计数器，电路每完成一个循环，输出F为 “1”。

比较[例7.1]和 [例7.2]，[例7.2]同步时序逻辑电路与[例7.1]的异步时序逻辑电路相比，虽然它们都是由n位处于计数工作状态的触发器组成，但是同步时序逻辑电路中往往含有门电路，因此电路结构比异步时序逻辑电路要复杂得多。异步时序逻辑电路通常采用的是串行计数，工作速度较低；同步时序逻辑电路由于各位触发器受同一时钟脉冲CP控制，决定各触发器状态 （J、K 状态）的条件并行产生，因此输出也是并行的，状态翻转速度比相应异步时序逻辑电路速度快得多。

表7.2　[例7.2]逻辑电路状态转换真值表