不同数码不仅可以表示不同数量的大小,而且还能用来表示不同的事物。用数码表示不同事物时,数码本身没有数量大小的含义,只是表示不同事物的代号而已,这时我们把这些数码称之为代码。
例如,运动员在参加比赛时,身上往往带有一个表明身份的编码,这些编码显然没有数量的含义,仅仅表示不同的运动员。
在数字系统中,为了便于记忆和处理,在编制代码时总要遵循一定的规则,这些规则就叫做码制。数字系统是一种处理离散信息的系统,这些离散的信息可能是十进制数、字符或其他特定信息,如电压、压力、温度或其他物理量。但是,计算机的数字系统只能识别和处理二进制数码,因此,各种数据要转换为二进制代码才能进行处理。
1.二—十进制BCD码
在数字系统的输入输出中普遍采用十进制数,这样就产生了用四位二进制数表示一位十进制数的方法,这种用于表示十进制数的二进制代码称为二—十进制代码 (BinaryCodedDecimal),简称为BCD码。
BCD码具有二进制数的形式以满足数字系统的要求,同时它又具有十进制的特点,即只有10种有效状态。在某些情况下,计算机也可以对这种形式的数直接进行运算。用四位二进制表示一位十进制数时,所编成的代码有24=16种组合状态,而一位十进制数只有0~9的10个数码,因此,从16个数码中任选出10个组成表示十进制的代码,方案显然有很多种。实用中,我们按照使用的方便与否,选择出其中真正有价值的、为数不多的几种,表4.5所示即为常用的几种二—十进制BCD代码。
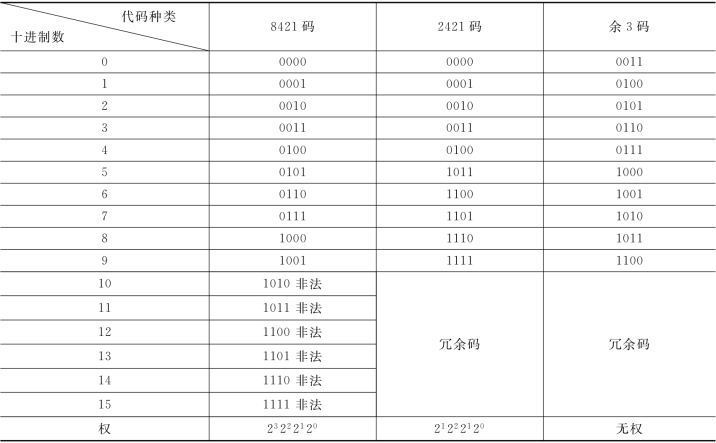
表4.5 常用的几种二—进制BCD码
 (https://www.xing528.com)
(https://www.xing528.com)
从表4.5中可看出,8421BCD码的位权从高位到低位分别为8、4、2、1固定不变,故称为8421BCD码,也称为恒权代码,是有权码中用得最多的一种。
2421码也是有权码中的一种恒权码。2421码的特点是码中的0和9、1和8、2和7、3和6、4和5的编码互为反码(即各位取反所得为反码)。
余3码是一种无权码。由于每一个余3码所表示的二进制数正好比对应的8421BCD码所表示的二进制数多余3,故而称为余3码。由表4.5还可看出,余3码中的0和9、1和8、2和7、3和6、4和5的编码也互为反码。
以上三种BCD码的代码只对应十进制的0~9的数值,剩余编码为无效码,无效码也叫做冗余码。
2.格雷码
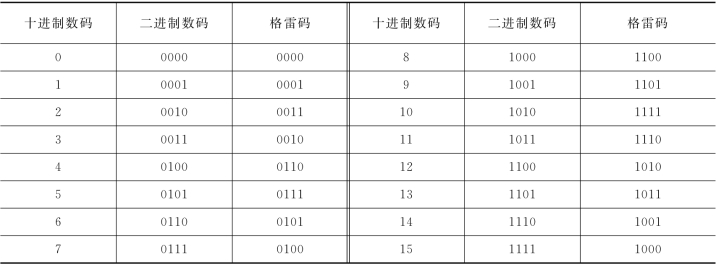
格雷码属于无权码,格雷码有多种代码形式,最常用的四位循环格雷码特点是:相邻两个代码之间仅有一位不同,其余各位均相同。当电路按格雷码计数时,每次状态更新仅有一位代码发生变化,从而减少了出错的可能性。格雷码不仅相邻两个代码之间仅有一位的取值不同,而且首、尾两个代码也仅有一位不同,构成一个 “循环”,故而也称为循环码。此外,格雷码还具有“反射性”,如0和15、1和14、2和13、……、7和8都只有一位不同,故而格雷码又称为反射码。表4.6为典型四位格雷码与十进制、二进制数码的比较。
表4.6 典型格雷码与十进制、二进制数码的比较
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




