集成运放的线性应用优化

当集成运放通过外接电路引入负反馈时，集成运放成闭环状态并且工作于线性区。运放工作在线性区可构成模拟信号运算放大电路、正弦波振荡电路和有源滤波电路等。

1.反相比例运算电路

图3.5所示为反相比例运算电路。其中RF为反馈电阻，跨接在输出和反相输入端之间，构成电压并联负反馈电路；Ri是输入电阻；RP是平衡电阻，为保证电路处于对称状态，就要使运放的反相输入端和同相输入端的外接电阻相等，即满足RP=RF∥Ri的条件；输入信号ui由反相端加入。

观察图3.5所示电路，由 “虚断”概念可得，通入RP的电流为零，因此运放的同相输入端电位可看作与 “地”电位相等。由 “虚短”概念又可得反相输入端的电位等于同相输入端的电位，即U-=U+= “地”电位。反相输入端并未接“地”却具有“地”电位的现象称为“虚地”。

由图3.5所示电路分析可知

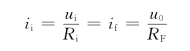
图3.5　反相比例运算电路

由上式可推出反相比例运算电路的闭环电压放大倍数为

式 （3.3）中负号说明输出电压u0与输入电压ui反相。可见，反相比例运算电路的闭环电压放大倍数实际上就是其比例运算常数。由式 （3.3）又可得出电路输出与输入的关系式为

显然，输出电压与输入电压之间的比例运算常数由反馈电阻RF和输入电阻Ri决定，与集成运放本身的参数无关。要想获得所需的输出、输入电压运算关系，只需选择合适的外接电阻元件即可，而且外接电阻的阻值精度越高，运放的精度和稳定性也越好。

当Ri=RF时，u0=-ui或Auf=-1时，表明输出电压与输入电压大小相等、极性相反，运放作一次变号运算，故也常把反相比例运算电路称为反相器。

2.同相比例运算电路

图3.6所示为同相比例运算电路。输入信号从同相输入端加入，反相输入端经R2接地，RF接在运放的输出端与反相输入端之间，构成电压串联负反馈电路。

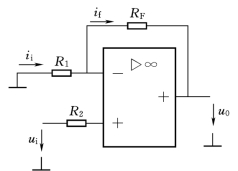
图3.6　同相比例运算电路

由理想运放的两条重要结论可推出：由于 “虚断”，通过R2的电流为零，因此，同相输入端电位U+=ui。由 “虚短”可知U-=U+=ui。

依据图3.6中各电压、电流的参考方向可得

由此，可得同相比例运算电路输出电压与输入电压之间的关系式为

式 （3.5）表明：输出电压与输入电压同相，电路的比例系数恒大于1，而且仅由外接电阻的数值来决定，与运放本身的参数无关。当外接电阻R1=∞或反馈电阻RF=0时，有

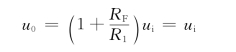
此时输出电压等于输入电压，同相比例运算电路在此状态下构成电压跟随器。

3.双端输入运算电路

双端输入运算电路如图3.7所示。双端输入运算电路实际上是一个差动输入运算放大器，为保证输入端平衡，电路中R1=R2，R3=RF。

实质上，双端输入运算电路是由反相输入和同相输入两种运算放大器组合而成。由于放大器工作在线性区，因此可用叠加定理分析电路的输出和输入关系。

首先令ui1=0，只考虑ui2单独作用下的情况。显然，这时的电路是一个同相输入运算电路，由图3.7可得同相输入端电位为

图3.7　减法运算电路

由 “虚短”可得

根据前面讨论的同相比例运算输出与输入的关系可得

因为R1=R2，R3=RF，所以上式可整理为

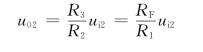(www.xing528.com)

再令ui2=0，只考虑ui1单独作用下的情况。显然，这时的电路是一个反相输入运算电路，反相输入运算电路总是存在“虚地”现象，由前面的讨论可得

根据叠加定理最后可得出

如果再有R1=RF，则

实现了输出对输入的减法运算。

4.微分运算电路

把反相比例运算电路中的输入电阻Ri用C1代替，就构成了微分电路，如图3.8所示。

微分电路当输入信号频率较高时，电容的容抗减小，放大倍数增大，因而对输入信号中的高频干扰非常敏感。

由理想运放的“虚断”和 “虚短”条件可得

因此

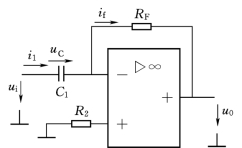
图3.8　微分运算电路

可见，微分电路的输出电压正比于输入电压对时间的微分。电路中的比例常数取决于时间常数τ=RFC1。当输入信号为矩形波电压时，输出信号为尖脉冲电压，如图3.9所示。

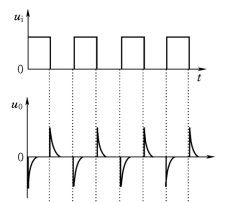
图3.9　微分电路的波形变换

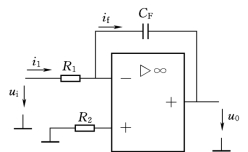
图3.10　积分运算电路

5.积分运算电路

只要把微分运算电路中的RF和C1的位置互换，就构成了积分电路，如图3.10所示。

由理想运放的“虚断”和 “虚短”条件可得

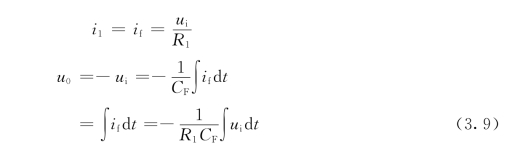
可见，输出电压u0正比于输入电压ui对时间的积分，其比例常数取决于积分时间常数τ=R1CF。式 （3.9）中的负号表示输出电压与输入电压反相。

6.集成运放线性应用实例

（1）应用实例1——测振仪。测振仪的组成框图如图3.11所示。

测振仪用于测量物体振动时的位移、速度和加速度。设物体振动的位移为x，振动的速度为v，加速度为α，则

图3.11中，速度传感器产生的信号与速度成正比，开关在位置“1”时，它可直接放大测量速度；开关在位置“2”时，速度信号经微分器进行微分运算再放大，可测量加速度α；开关在位置“3”时，速度信号经积分器进行积分运算再一次放大，又可测量位移x。在放大器的输出端，可接测量仪表或示波器进行观察和记录。

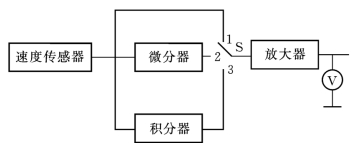
图3.11　测振仪组成框图

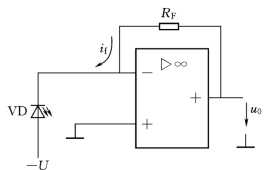
图3.12　光电转换电路

（2）应用实例2——光电转换电路，如图3.12所示。

光电传感器有光电二极管、光敏电阻、光电三极管和光电池等，它们都是电流器件。光电转换电路在光照作用下产生电流，将光信号转换成电信号，经放大后即可进行检测与控制。

光电二极管的结构在前面讲过，也是由一个PN结构成的，只是其PN结面积较大，以增加受光的面积；PN结的结深很浅（小于10-6m），可提高光电转换效率。

光电二极管工作在反向状态。无光照时，其反向电流一般小于0.1μA，常称为暗电流。光电二极管的反向电阻很大，高达几个兆欧。有光照时，在光激发下，反向电流随光照强度而增大，称为光电流，这时的反向电阻可降至几十欧以下。在图3.12示电路中，有光照时产生的光电流if，流经路径为u0→RF→VD→-U，这时集成运放的输出电压为u0=ifRF。