中等复杂镜头设计实例分享

显微物镜中的李斯特（Lister）物镜是中倍显微物镜的基本结构，它是由两组双胶合透镜组成的，它的数值孔径NA约为0.3，属于孔径较大的镜头。放映物镜中的四片物镜可以看成是匹兹瓦（Petzval）物镜的变型，匹兹瓦物镜的基本结构也是由两组双胶物镜组成的，它们的相对孔径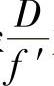为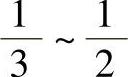，也是孔径较大的镜头。双高斯（Gauss）物镜是摄影物镜中的典型结构，普通的双高斯物镜一般是四组六片，中间两组胶合厚透镜对称放置，光阑居中，最外面两边各有一块正光焦度单片。它的相对孔径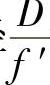约为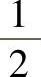，它的全视场2ω约为40°，是孔径和视场都比较大的镜头。

结构大致由4～6片玻璃组成，光学特性或者孔径较大，或者孔径和视场都比较大的这些镜头称为中等复杂镜头。

李斯特物镜、匹兹瓦物镜和双高斯物镜是光学镜头中应用很广泛的结构型式，这类镜头的优化设计是光学设计的初学者们应该做的一部分练习。

本章列举这几类物镜的八个优化设计实例，前两个是李斯特物镜设计例。康拉弟（Conrady A.E.）配合法是设计李斯特物镜的一个基本方法，也是一个很有成效的方法，不足之处在于没有考虑像散的消除问题。这里，在设计第一个李斯特物镜时，对康拉弟配合法做一些改进，改进之一在于配合过程中就加进优化，简化初始解的求解过程；改进之二在于优化设计时不仅要消除球差、彗差和位置色差，而且要消除像散。设计的第二个李斯特物镜以现成的结果为基础进行优化设计，也是不仅要消除球差、彗差和位置色差，而且要消除像散。(www.xing528.com)

第三个设计实例是一个四片的放映物镜，它的结构可以看成是匹兹瓦物镜的变型。设计时先由初步的光焦度分配开始，再分步选择各透镜的初步形状，构成一个初始结构，然后再优化设计出可用的结果。第四个设计实例是以第三个实例的初始结构为基础，采用不同的评价函数优化设计出结果。第五个设计实例是以第三个实例的结果为基础，分裂其中的部分镜片使其复杂化，进一步改善放映物镜的像质。

第六、第七和第八个设计实例都是双高斯摄影物镜。第六个设计实例取之于ZEMAX程序中附带的范例，设计时将它的全部半径破坏掉，将它的厚度做适当的破坏，采用范例选用的玻璃材料，然后再逐步优化成一个像质与范例可以相比的优良结果。第七个设计实例从一个像质很差，大量违反边界条件的初始结构开始，经过逐步优化，给出一个像质可与OSLO程序中附带的范例相比的优良结果。第八个设计实例的初始结构是一个失效的专利，经过逐步优化，给出一个像质可与《光学系统设计》（Optical System Design）（参考文献[5]）中的范例相比的优良结果。