用旋转矢量表示同频率正弦交流电

实训与思考4

◆已知两正弦交流电压

u₁=3sin314tV

试求总电压u=u₁+u₂的解析式。

◆已知上述两正弦交流电压的波形如图5-14所示，试求总电压u的波形图。

其实要完成上述的实训与思考的要求，没有较好的数学知识支持，是很难解题的。这是因为

同学们用现有的知识解题不仅是有困难的，而且也比较繁琐。而用波形图求解的结果如图5-15所示，也同样不怎么好操作。可见，解析式和波形图对正弦交流电进行加、减运算都不方便，那么有方便的解决方法吗？为此，引入第三种方法，即用旋转矢量来表示正弦交流电。

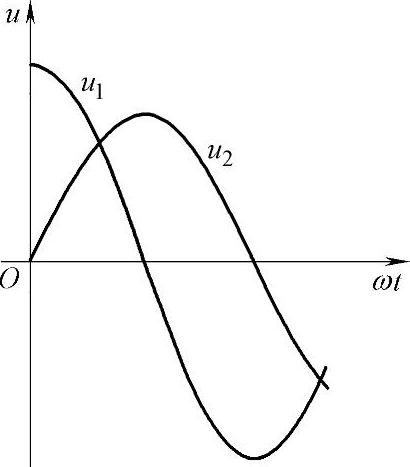
图5-14 两正弦交流电压的波形图

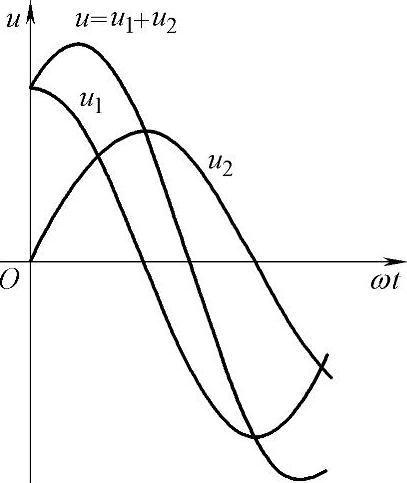
图5-15 用波形图求总电压

旋转矢量不同于力学中的空间矢量，它是随时间变化的矢量，在空间没有方向。它的加、减运算服从平行四边形法则。

正弦量的旋转矢量是以坐标原点O为端点做一条有向线段，线段的长度为正弦量的最大值（如I_m、U_m、E_m），旋转矢量的起始位置与x轴正方向的交角为正弦量的初相φ₀，它以正弦量的角频率ω为角速度，绕原点O逆时针匀速转动，即在任意时刻t，旋转矢量与x轴正半轴的交角为ωt+φ₀。则在任一时刻，旋转矢量在纵轴上的投影就等于该时刻正弦量的瞬时值。正弦交流电的旋转矢量与对应的波形图之间的关系，如图5-16所示。

图5-16 正弦交流电的旋转矢量与对应的波形图之间的关系

这样，就可以把某个正弦交流电用旋转矢量来表示。或者说，确定了正弦交流电的三要素，就确定了正弦交流电的旋转矢量。为了区别一般的空间矢量，用最大值符号（大写字母带下标“m”）上加“.”或黑体字表示。如、、分别表示正弦交流电流、电压、电动势的最大值旋转矢量，如图5-17a所示。

同频旋转矢量在坐标系中以同样的角速度旋转，各旋转矢量之间的交角反映彼此之间的相位差。相位差不变，相对位置保持不变，各个旋转矢量是相对静止的。因此，将它们当作静止情况处理，并不影响分析和计算的结果。所以，只有正弦量才能用旋转矢量表示，只有同频率正弦量才能借助于平行四边形法则进行旋转矢量的加、减运算。

初始位置的旋转矢量视为正弦交流电的相量表示法，对应的旋转矢量图称为相量图。有向线段的长度等于正弦量最大值的相量称为最大值相量。在旋转矢量图上省去坐标和旋转速度是相量图的习惯画法，如图5-17b所示。

图5-17 正弦交流电的旋转矢量和相量

几个同频率的正弦量都用相量表示，画在同一个坐标系中，不仅能直观地描述各个正弦量的大小和相互间的相位关系，而且能利用平行四边形法则进行加、减运算，非常方便。

在实际应用中，常采用有效值旋转矢量。这样，旋转矢量图中的有向线段的长度就变为正弦量的有效值。有效值旋转矢量用有效值符号（大写字母）上加“.”或黑体字表示。如正弦交流电流、电压、电动势的有效值旋转矢量分别表示为、、。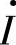

图5-18 相量图(www.xing528.com)

如图5-18所示为两个正弦交流电动势相加的相量图，做图步骤是首先按画图区域的大小确定标度和参考起点，然后按正弦交流电的三要素画出各相量，最后利用平行四边形法则进行加、减运算，按运算结果写出正弦交流电的解析式。

【例5-6】按已知条件求做电动势、电压、电流的相量图。已知正弦交流电的解析式为，，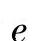

解：

1）为了做图方便，取电动势、电压、电流的有效值来做图。

2）做基准线。

3）取标度。

4）以各正弦量的有效值作为相量的长度，以各初相作为相量与横坐标的夹角（坐标可以省去）做图，如图5-19所示。

【例5-7】已知两正弦交流电压u₁=3sin314tV，u₂=4sin（314t+π/2）V，试用相量图求总电压u=u₁+u₂的解析式。

解：

分别做出两正弦交流电的相量图，并用平行四边形法求做总电压的相量图，如图5-20所示。

图5-19 例5-6图

图5-20 例5-7图

根据总电压的相量图用尺子量出或利用几何关系求出总电压的大小和初相位。

测量或计算的结果是总电压的最大值为5V，初相位为37°。

这样就能写出总电压的解析式为

u=u₁+u₂=5sin（314πt+37°）V

实训与思考5

◆根据图5-21所示的正弦交流电流的相量图，写出总电流i的解析式。

提示：用两个正弦量Oa与Ob相加的方法去思考。

根据图5-21所示的平行四边形Oacb可知，对角线Oc的长就是相加后的正弦交流电流i的最大值，Oc与x轴（可以省去不画）的夹角就是正弦交流电流i的初相位。

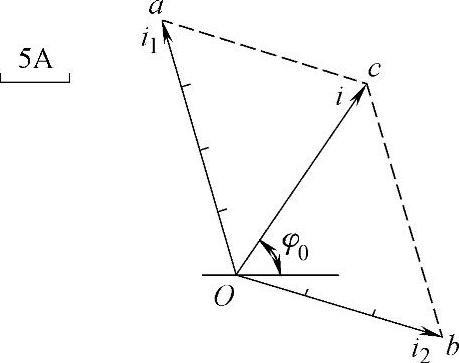
图5-21 实训与思考5图