正弦交流电的相位和相位差详解

1.相位

图5-6所示为交流发电机线圈以ω角速度旋转时线圈平面与中性面的角度变化情况。若起始时刻线圈平面与中性面的夹角为φ₀，那么，t时刻线圈平面与中性面的夹角应为（ωt+φ₀），我们把（ωt+φ₀）称为正弦交流电的相位。显然，t=0时，相位等于φ₀，φ₀称为初相位，简称初相。初相位反映正弦交流电起始时刻的状态（电角度）。

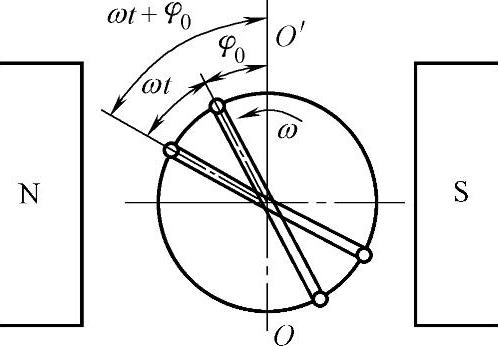
图5-6 正弦交流电的相位

实验表明，在t时刻发电机所发出的感应电动势的瞬时值表达式为e=E_msin（ωt+φ₀），它表示了正弦交流电动势与时间的关系。

初相的大小和时间起点的选择有关，习惯上用绝对值小于π的角度来表示初相位。例如把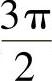写成。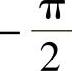

相位是表示正弦交流电在某一时刻所处状态的物理量。它不仅决定交流电瞬时值的大小和方向，还能反映正弦交流电的变化趋势。这与数学中的正弦函数变化规律分析类同。

2.相位差

如图5-7所示，设两个同频率的交流电i₁=I_m1 sin（ωt+φ₀₁），i₂=I_m2sin（ωt+φ₀₂）。由于它们的初相不同，因此在某一时刻的相位也不同。两个同频率的正弦交流电，任意时刻的相位之差称为相位差，用φ来表示（当特别需要强调次序时，可用下标来说明，如φ₁₂等），即

φ=（ωt+φ₀₁）-（ωt+φ₀₂）=φ₀₁-φ₀₂ （5-3）

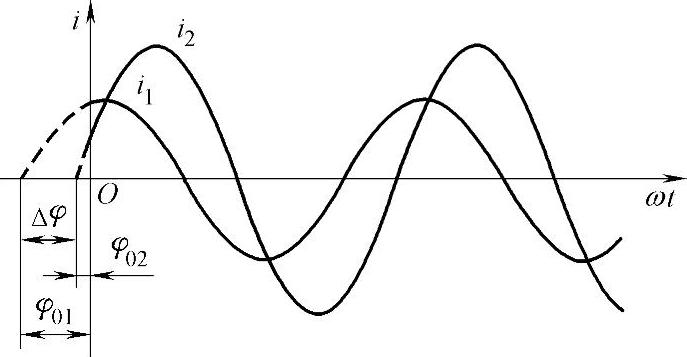
图5-7 两个同频率正弦交流电的相位差

由此可见，两个同频率的正弦交流电的相位差就是初相之差。它与时间无关，在正弦量的变化过程中的任意时刻都是一个常数。它表明了两个正弦量之间在时间上的超前或滞后的关系。在实际应用中，规定用绝对值小于π的角来表示相位差。

通常两个正弦量的相位关系有五种。

1）当φ_ui＞0时，称u超前i，如图5-8a所示；

2）当φ_ui＜0时，称u滞后i，如图5-8b所示；

3）当φ_ui=0时，称u与i同相，如图5-8c所示；

4）当φ_ui=±π时，称u与i反相，如图5-8d所示；

5）当φ_ui=±π/2时，称u与i正交，如图5-8e所示。

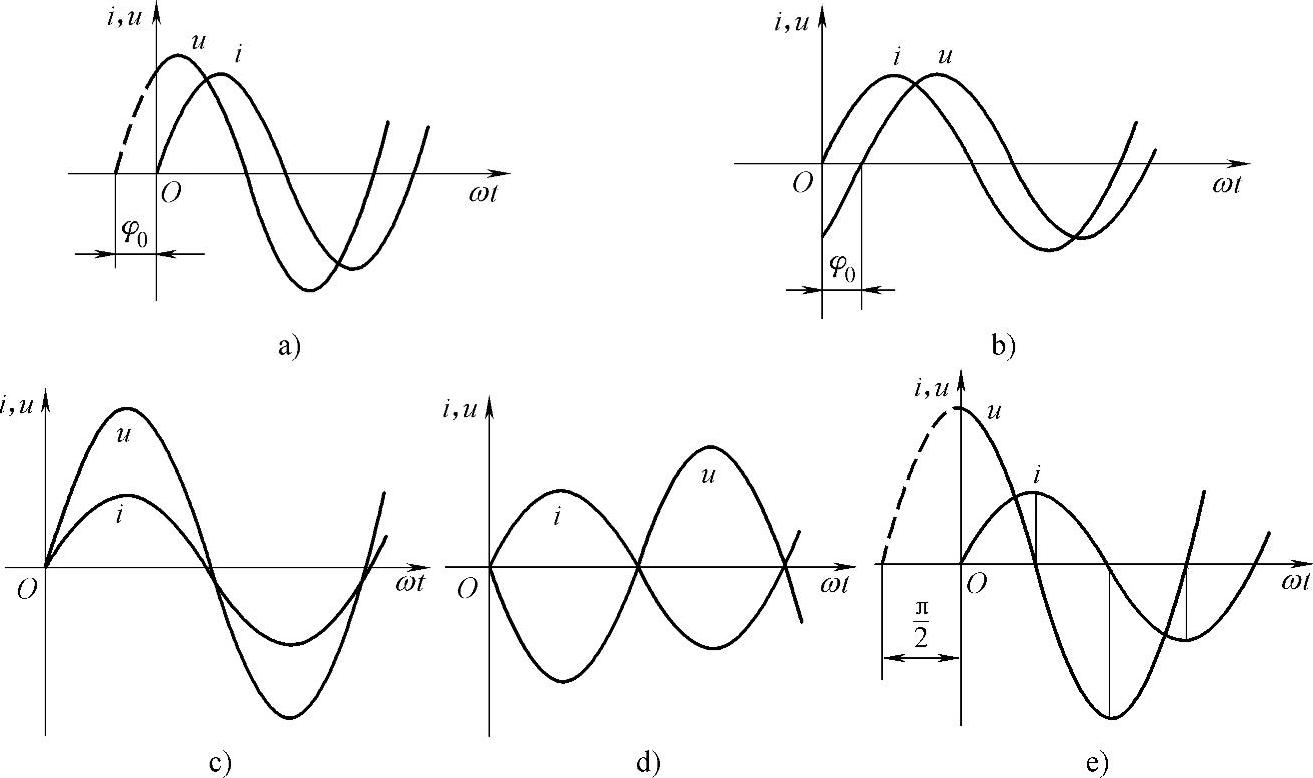
图5-8 两个同频率正弦交流电的相位关系(www.xing528.com)

值得注意的是，当i₁超前i₂时，不能理解为i₁比i₂先产生，而是表明当电流i₁达到最大值时，电流i₂要过φ₁₂/ω以后，才能达到最大值。

实训与思考3

◆两人合作，按图5-9a所示分别将两台手摇发电机接上电流计，以相同的频率转动线圈，观察电流计指针的摆动，如图5-9b所示判断哪个电流相位超前。

方法如下：

两电流计的指针最大偏转都能到达“5”，请两位同学（最好声音有明显区别的）

观察指针运动，一位看表1，一位看表2，当指针到“5”时喊“到”，根据两位同学

喊声的先后，可以判断哪个电流相位超前。

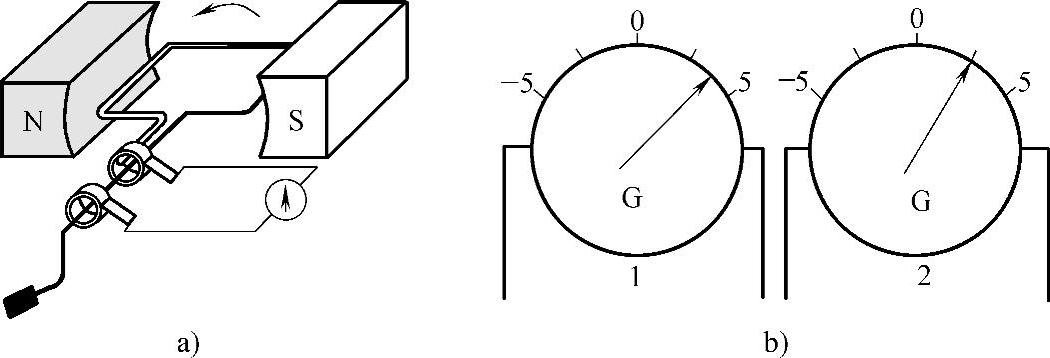
图5-9 两相同频率的正弦交流电的相位关系实验

a）手摇发电机原理图 b）电流计表面指针摆动示意图

【例5-2】如图5-10所示，已知i₁=3sin（314t+30°）A，i₂=5sin（314t-30°）A，求i₁与i₂各自的相位、初相以及它们的相位关系。

解：由已知条件可知，i₁的相位为

φ₁=314t+30°，初相φ₀₁=30°

i₂的相位为

φ₂=314t-30°，初相φ₀₂=-30°

i₁与i₂的相位差为

φ=30°-（-30°）=60°＞0

i₁与i₂的相位关系是：i₁超前i₂60°。

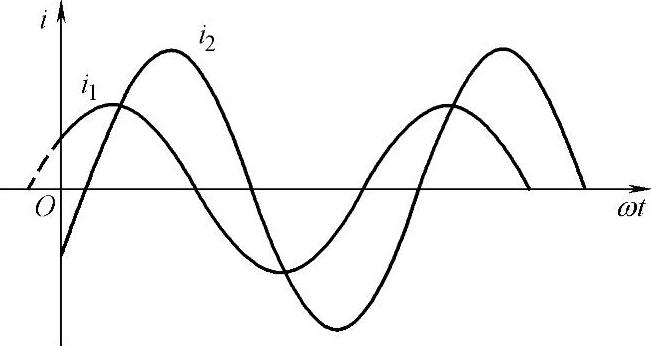
图5-10 例5-2图