优化设计实例：5倍增距显微镜

设计双胶物镜的关键之一是选好玻璃对，设计时可以用PW法得到初始解，然后再上计算机优化，例如前面设计-5^×显微物镜例1时就走过了这样一个过程。也可以不用PW法求解初始结构，先初步选用一对玻璃，大致分配光焦度后直接在计算机上优化，在优化过程中的适当阶段将玻璃材料作为变量参与优化，直至得到一个好的结果。下面用后一个办法设计这个-5^×显微物镜。

1.初选玻璃对的原则

玻璃对通常选择折射率差较大、色散差也较大的常用玻璃。例如这里选用（K9，F5）这对玻璃，它们的折射率和阿贝数分别是K9（1.51637，64.07）、F5（1.62435，35.92）。

2.分配光焦度，初步确定透镜半径

由前面的计算知道，物镜前光路中的平板玻璃产生的CⅠ很小，可以先忽略以使计算简便，如此可联列出如下的消除位置色差方程和合成光焦度方程：

式中，φ是“-5^×显微物镜”的光焦度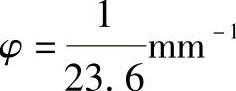，；φ₁和φ₂分别是组成-^5×显微物镜两块镜片的光焦度；ν₁=64.07，ν₂=35.92。

解式（2-6）得

φ₁=0.0963157mm^-1

φ₂=-0.0539428mm-1

设第一块镜片的形状为相等半径值的双凸透镜，由薄透镜焦距公式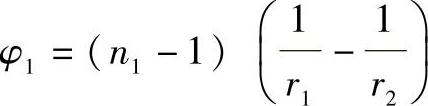并代入K9玻璃的d光折射率n₁=1.51637可得

r₁=10.721mm

r₂=-10.721mm

同样，由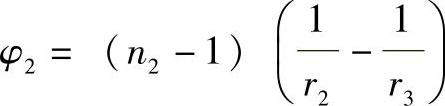可得

r₃=-145.821mm

式中，n₂是F5玻璃的折射率，n₂=1.62435。

3.优化

以上述初步确定的玻璃材料数据，计算出的半径作为初始参数，并将第一块镜片的厚度仿照前面的结果初步定为2.7mm，第二块镜片的厚度定为1mm，以此作为初始结构上计算机进行优化。初始结构参数见表2-26，球差曲线如图2-76所示，点列图如图2-77所示，OSC′的值由弧矢彗差K_s′间接算出为-0.014。

表2-26 -5^×显微物镜例2的初始结构参数

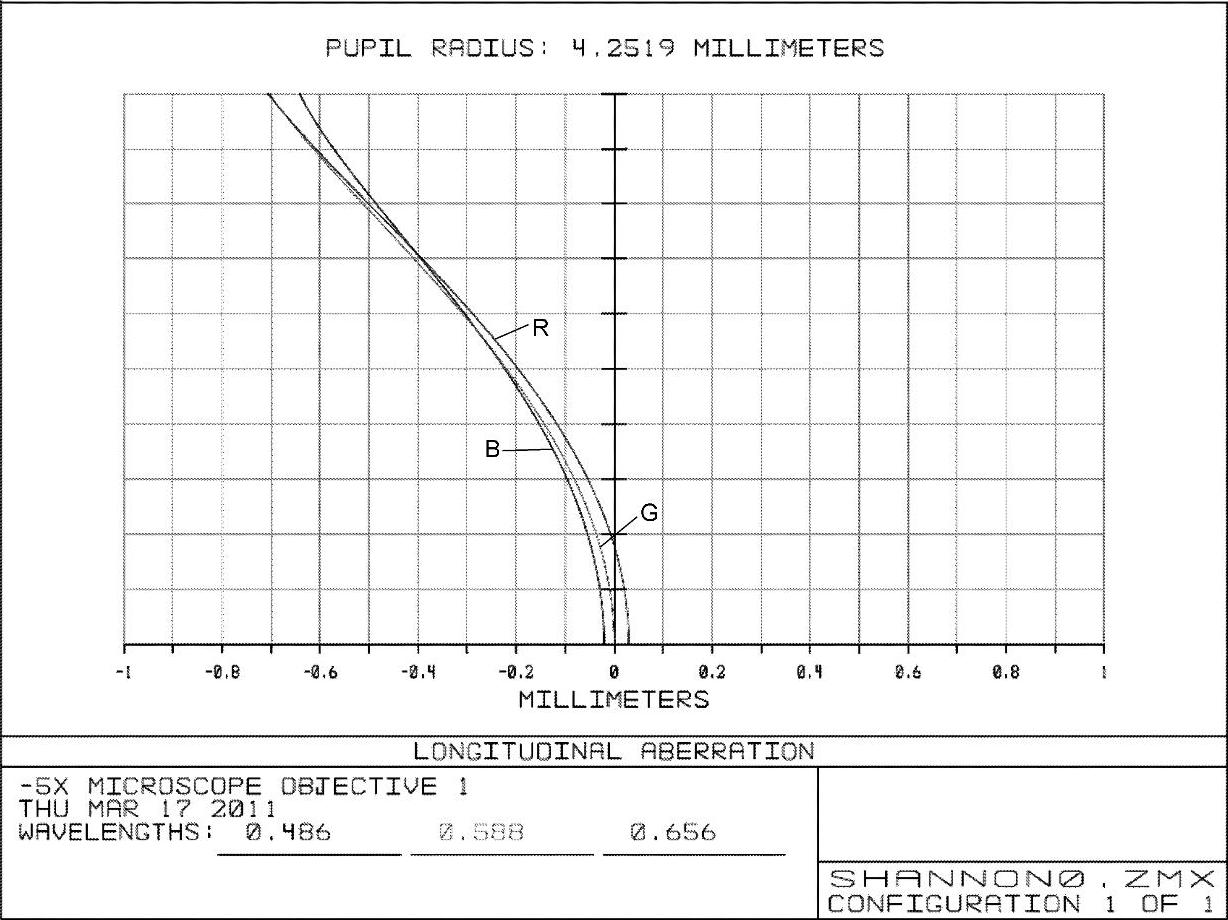
图2-76 -5^×显微物镜例2初始结构的球差曲线

（1）第1步优化 由图2-76看出，初始结构的球差与位置色差必须校正，需要优化。

优化时，选择物镜的前两个折射面半径作为变量，用物镜的第三个折射面半径保证数值孔径NA=0.15。与前例同样，将轴上点全孔径的轴向球差“LONA”（λ=0.587652μm，Zone=1）、轴上点0.707孔径的位置色差“AXCL”（λ₁=0.48613270μm，λ₂=0.65627250μm，Zone=0.707）、以及全孔径的正弦差“OSCD”（λ=0.587652μm，Zone=1）加入到评价函数中，权重都取1，目标值都取0。评价函数用操作语句括号写出如下：

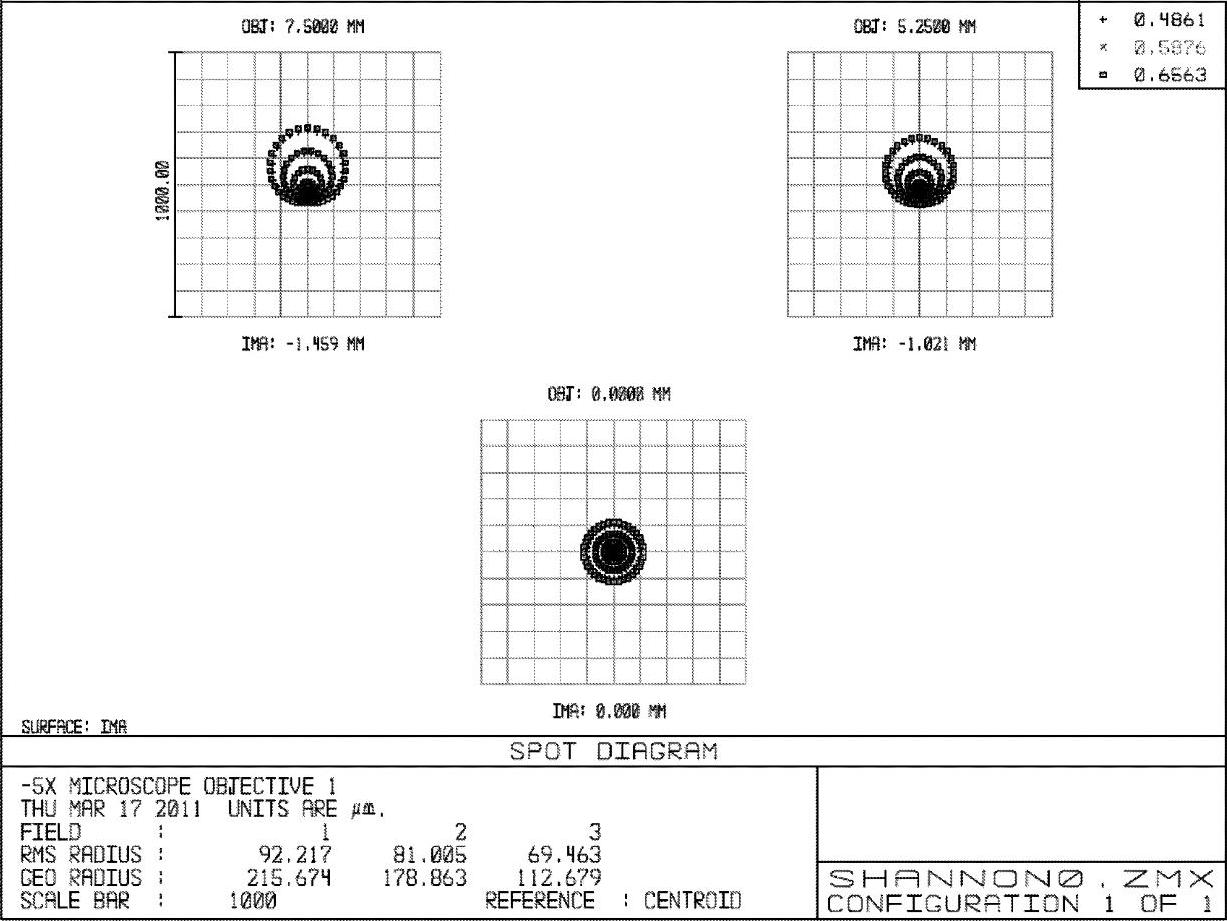
图2-77 -5^×显微物镜例2初始结构的点列图

{LONA（Wave；Zone）；Target，Weight}⇒{LONA（2；1）；0，1}

{AXCL（Wave1，Wave2；Zone）；Target，Weight}⇒{AXCL（1，3；0.7）；0，1}

{OSCD（Wave；Zone）；Target，Weight}⇒{OSCD（2；1）；0，1}

优化后的结构参数见表2-27，球差曲线如图2-78所示，点列图如图2-79所示，优化后的OSC′为0.013。如前述，在ZEMAX程序中，优化后评价函数中“OSCD”的当前值就是优化后的OSC′值。

表2-27 -5^×显微物镜例2第1步优化后的结构参数(www.xing528.com)

（2）第2步优化 从像差曲线图2-78看到，经第1步优化后，球差和位置色差校正的较好。但物镜的OSC′值为0.013，彗差不好。

现将第一块镜片的材料作为变量。将物镜的第一片玻璃改为变量的操作过程如下：

在主窗口中打开的透镜数据编辑器表上，将玻璃材料改为“模型玻璃（model）”→右键单击该片玻璃的折射率→将出现在窗口中的n_d和ν_d改为变量→OK。

值得指出，一般来说将玻璃材料作为变量时要加边界条件来限制折射率和阿贝数在合理的范围内变动，但考虑到现经第1步优化后像质已接近公差允限，估计材料折射率和阿贝数变动不大即可满足要求，所以就暂不在评价函数中加入限制材料折射率和阿贝数变动的边界条件了。

选择物镜第一个折射面半径和第二个折射面半径作为变量，令第三个折射面半径保证物镜数值孔径NA=0.15。选用与第1步优化时同样的评价函数进行第2步优化，组成评价函数的操作语句括号如下：

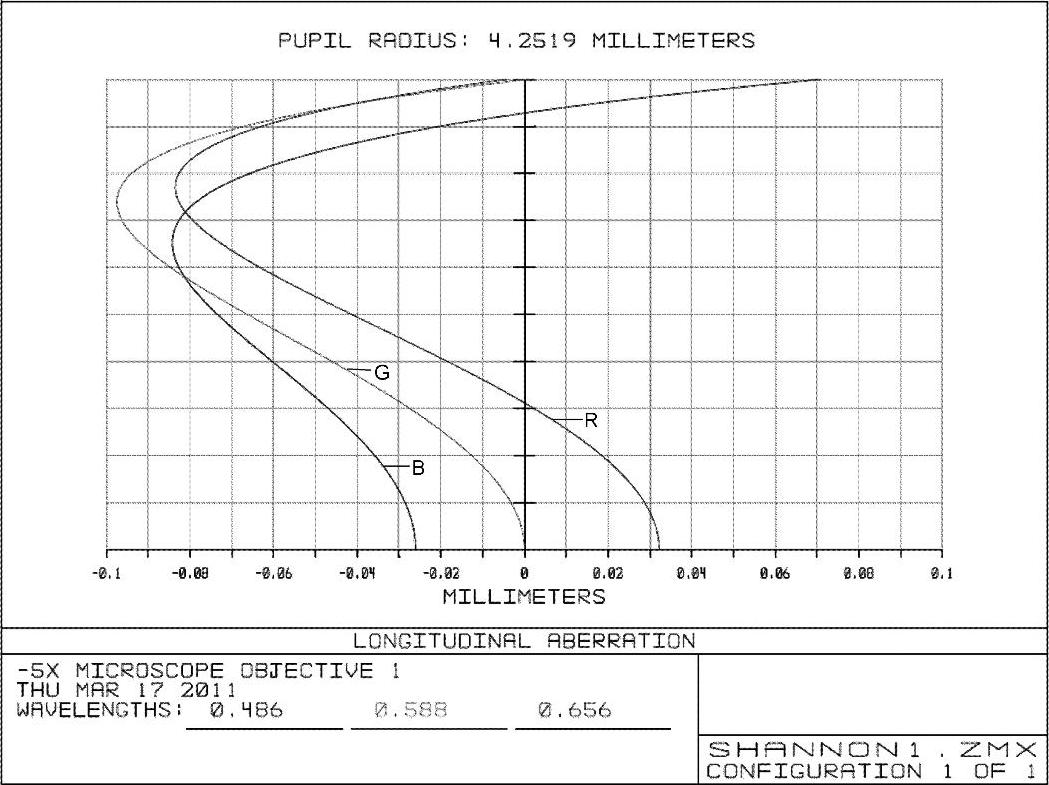
图2-78 -5^×显微物镜例2第1步优化后的球差曲线

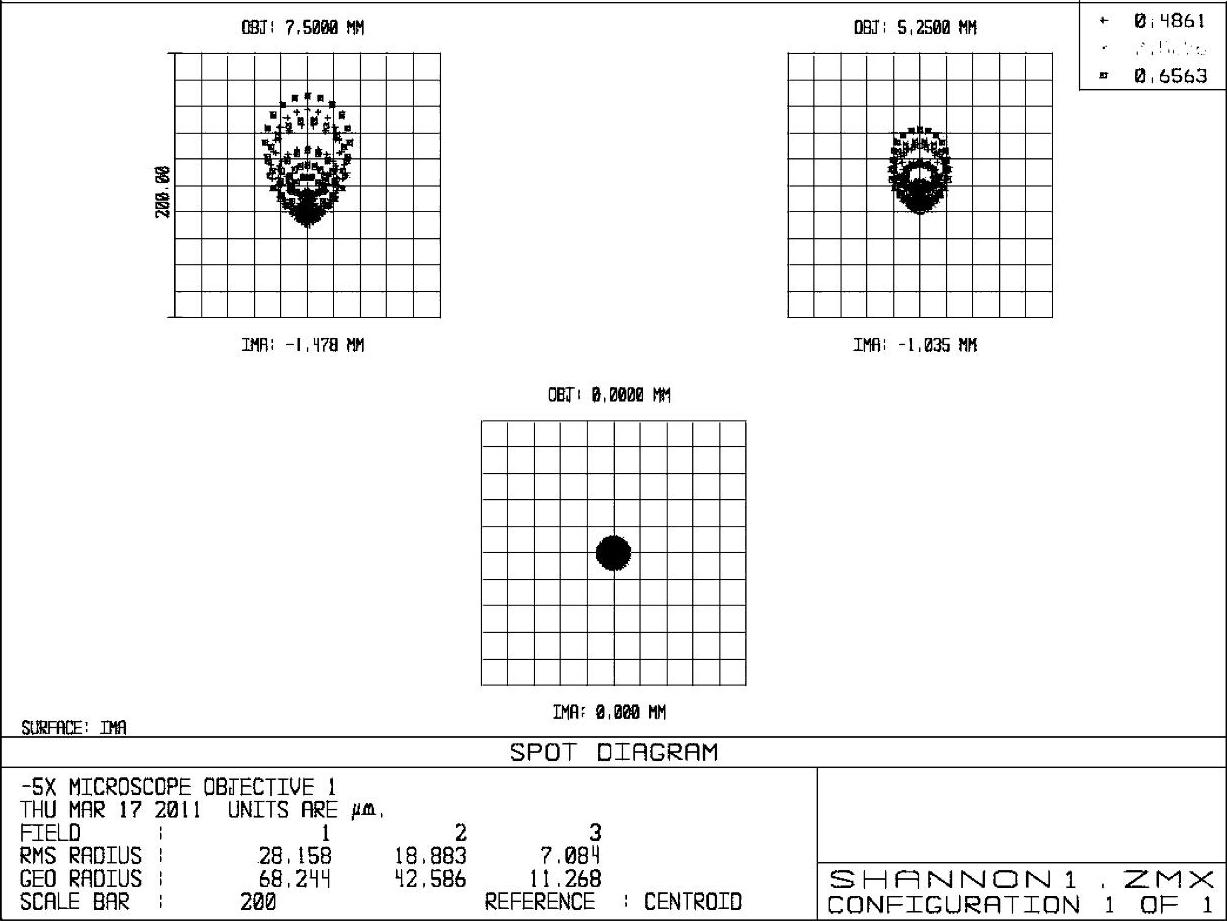
图2-79 -5^×显微物镜例2第1步优化后的点列图

{LONA（Wave；Zone）；Target，Weight}⇒{LONA（2；1）；0，1}

{AXCL（Wave1，Wave2；Zone）；Target，Weight}⇒{AXCL（1，3；0.7）；0，1}

{OSCD（Wave；Zone）；Target，Weight}⇒{OSCD（2；1）；0，1}

第2步优化后的球差曲线如图2-80所示，点列图如图2-81所示，由评价函数中“OSCD”的当前值知优化后的OSC′的值为零。

（3）第3步优化 第2步优化后，尽管像差已校正好了，但由于将玻璃材料作为了变量，又由于在优化过程中这个变量是作为一个连续变量对待的，所以第2步优化后的材料折射率和阿贝数在现实中不一定正好找到，这就要用实际玻璃就近替代优化后的“模型玻璃”。玻璃替代的操作如下：

右键单击模型玻璃折射率，选择替代（substitute）→OK。

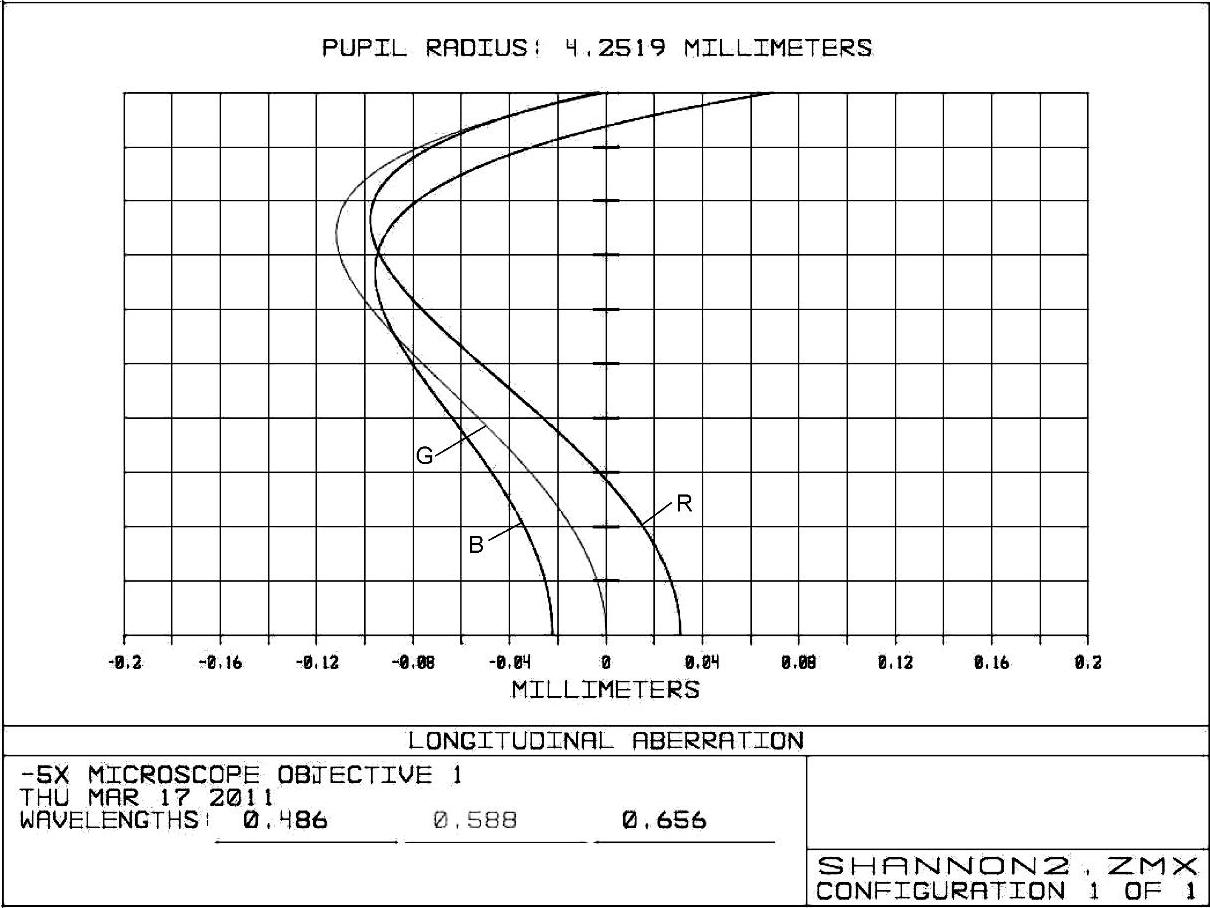
图2-80 -5^×显微物镜例2第2步优化后的球差曲线

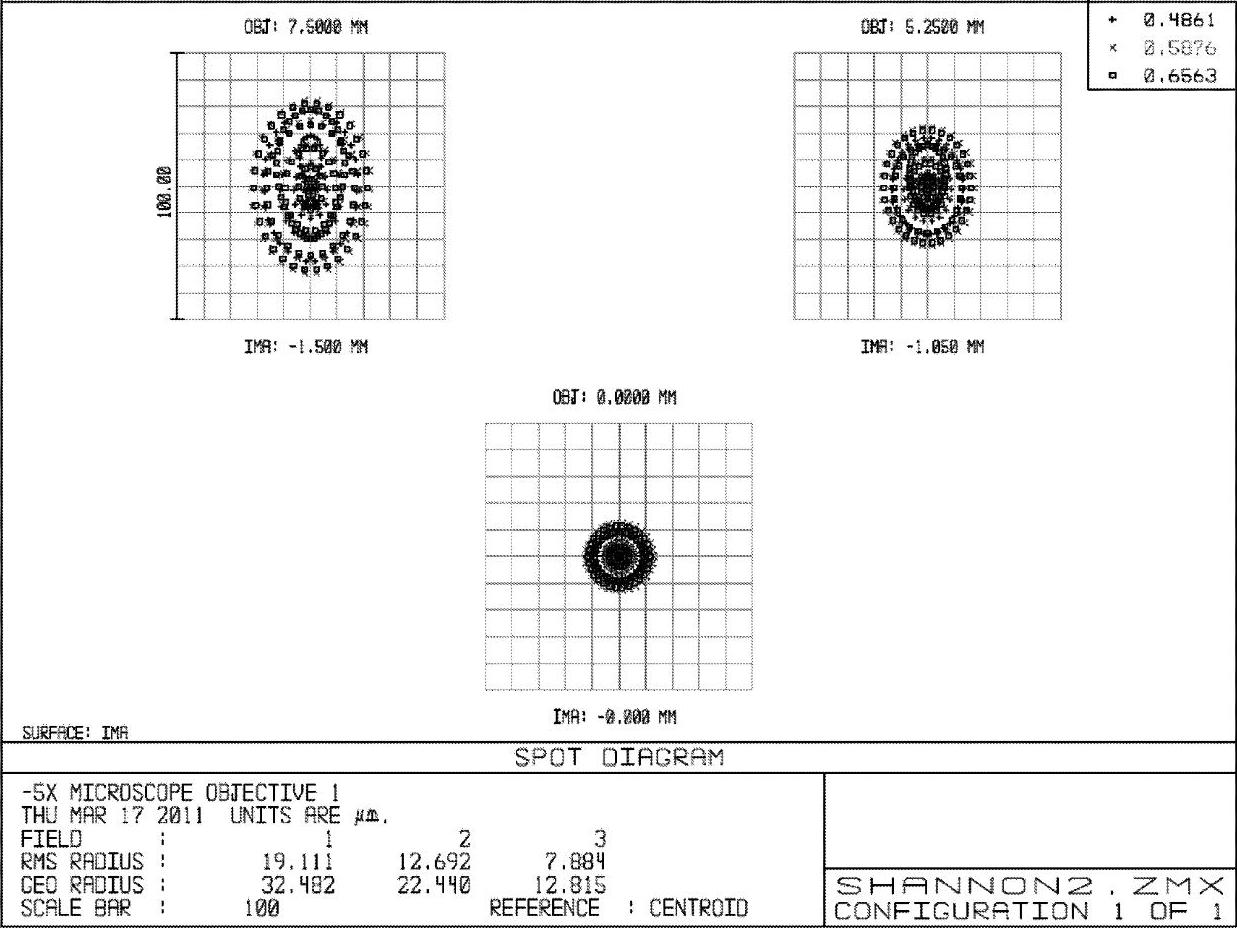
图2-81 -5^×显微物镜例2第2步优化后的点列图

现选择出的替代玻璃是QK3（1.48746，70.04），然后就将笫一块镜片的材料确定为QK3，不再作为变量。并以此为基础，选择物镜的第一个折射面半径和第二个折射面半径作为变量，让第三个折射面半径保证物镜的数值孔径。选用第1步优化时所用的评价函数进行第3步优化。优化后的结构参数见表2-28，球差曲线如图2-82所示，点列图如图2-83所示，OSC′的值为-0.0016。

表2-28 -5^×显微物镜例2第3步优化后的结构参数

从像差曲线和像差数据看出，这个镜头的质量已经符合2.3.2节所列像差公差的要求，设计结果是好的。说明例2确定初始结构的办法是行得通的。

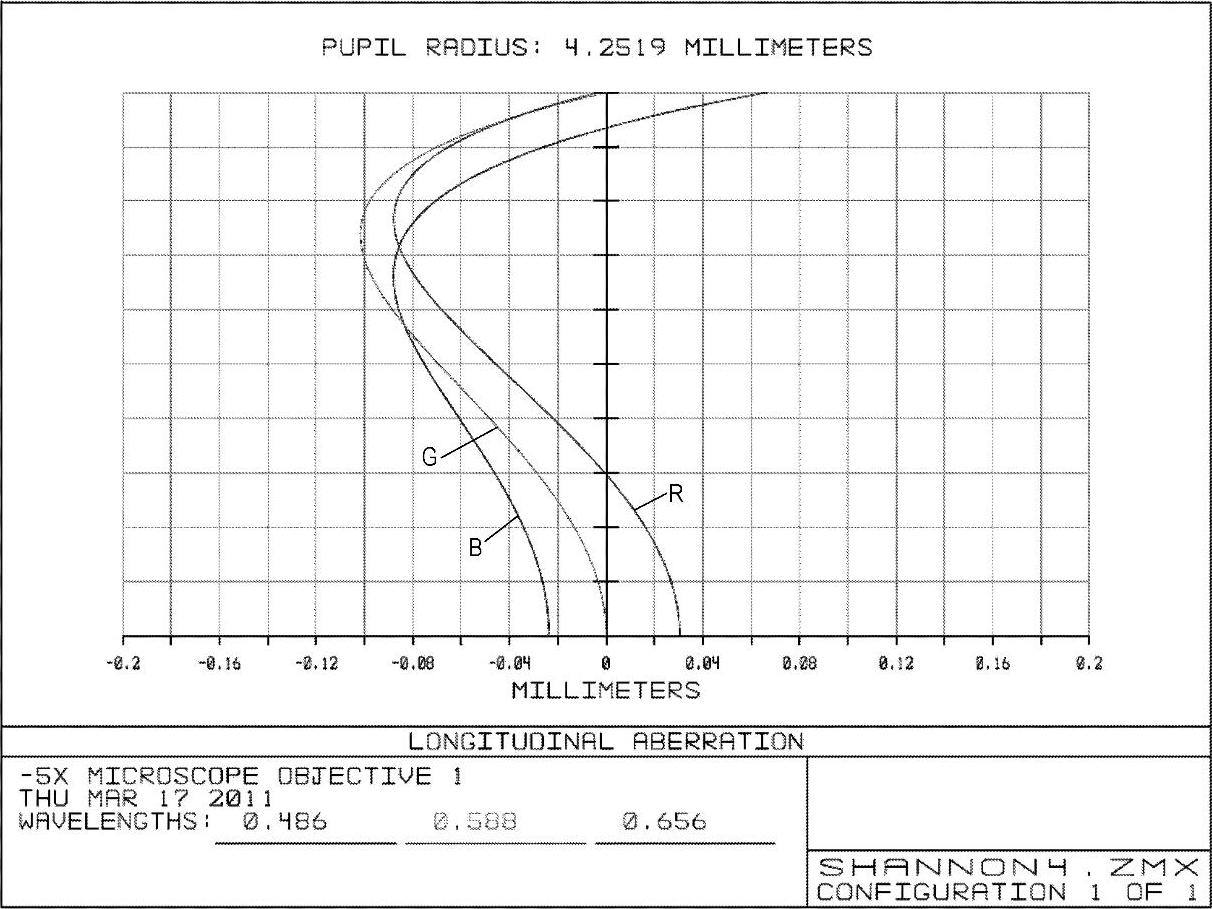
图2-82 -5^×显微物镜例2第3步优化后的球差曲线

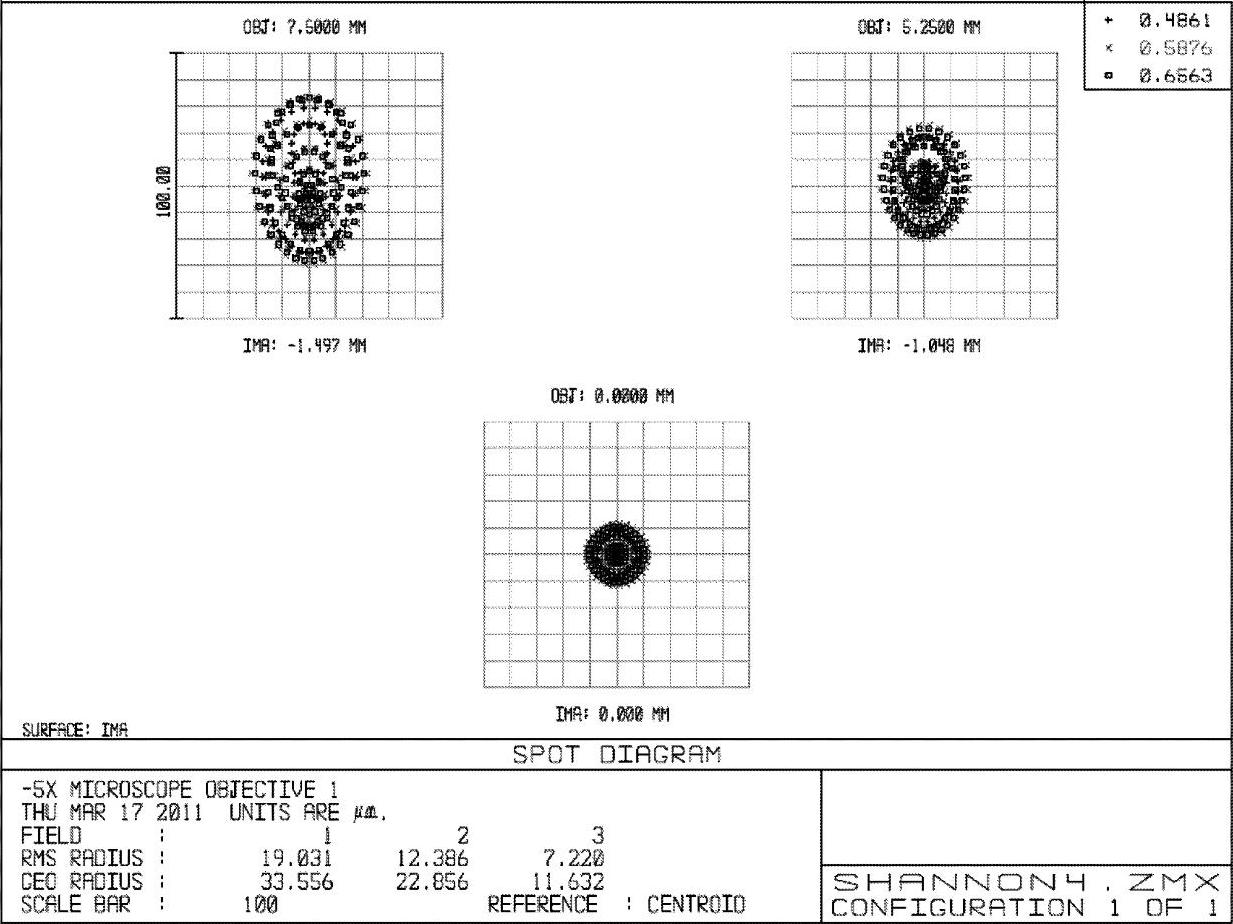
图2-83 -5^×显微物镜例2第3步优化后的点列图

[1]参见全国自然科学名词审定委员会编写的《物理学名词》第68页（见参考文献[27]）