电容器串联实验及其安全问题探究

将两只或两只以上的电容器首尾依次相连，接成一个无分支的电路的连接方式称为电容器的串联，如图3-8所示。

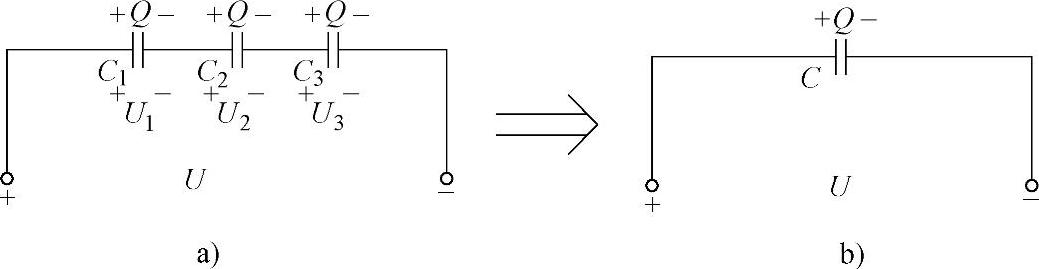
图3-8 电容器串联电路

当单独一只电容器的耐压不能满足电路要求，而它的容量又足够大时，可将几只电容器串联起来，再接到电路中使用。如图3-8所示，如果图3-8b中的电容C与图3-8a中的三只串联电容的总效果相同，则电容C为三只串联电容的等效电容。

实训与思考5

1）按图3-9所示电路（1）连接电路。合上开关，石英小闹钟开始走动。一段时间后，小闹钟停止走动。用电压表测量电容器两端的电压。在表3-4中记录小闹钟走动的时间和电容器两端的电压。

2）按图3-9所示电路（2）连接电路。用电容表测出串联后的总电容量。合上开关，小闹钟开始走动。一段时间后，小闹钟停止走动。用电压表分别测量两只电容器两端的电压。在表3-4中记录小闹钟走动的时间和电容器两端的电压。

3）按图3-9所示电路（3）连接电路。用电容表测出串联后的总电容量。合上开关，小闹钟开始走动。一段时间后，小闹钟停止走动。用电压表测量电容器两端的电压。在

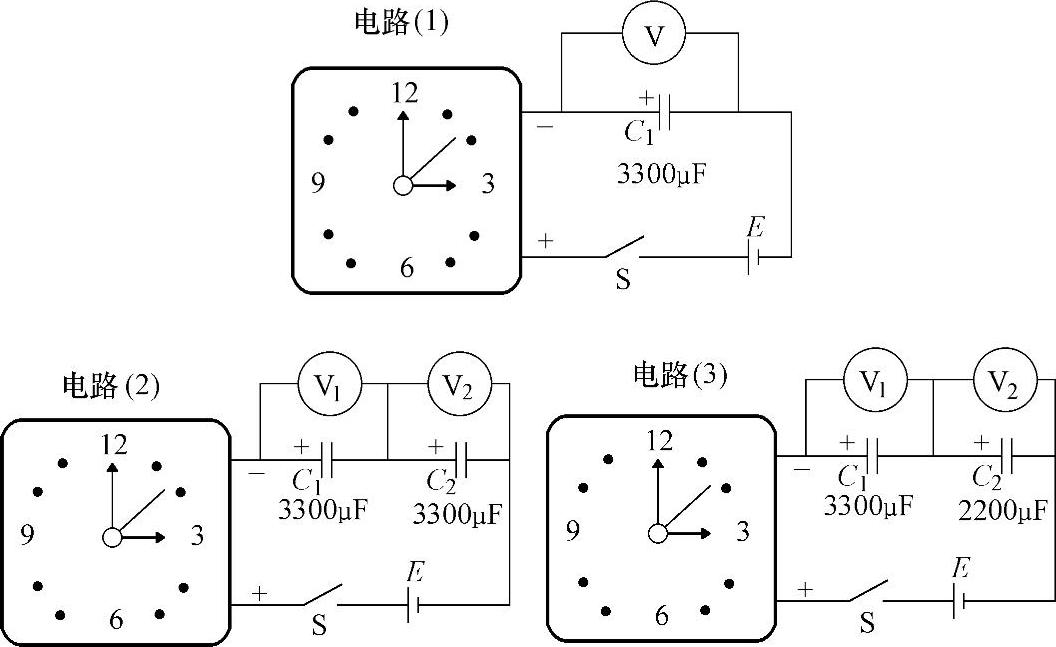
图3-9 电容器的串联实验

表3-4 中记录小闹钟走动的时间和电容器两端的电压。

表3-4 电容器串联实验记录

思考分析：

◆电容器串联后总的电容量如何变化？储存电荷的能力如何变化？____

◆电容器串联电路中，电容器两端的电压与电容量有何关系？____

下面来分析电容器串联电路的特性。如图3-8所示，设有三只电容器组成串联电路，将电源接到这个电容器组两端的两个极板上，当给电容器C₁左面的极板充上电荷量+Q时，则右面的极板由于静电感应而产生电荷量-Q，这样电容器C₂左面的极板就出现电荷量+Q；右面的极板因静电感应而产生电荷量-Q，同理，电容器C₃左面的极板带电荷量+Q，右面的极板带电荷量-Q。因此，串联电容器组中的每一只电容器都带有相等的电荷量，即

Q=Q₁=Q₂=Q₃ （3-4）

根据电容的定义式显然可得，每个电容器两端的电压为

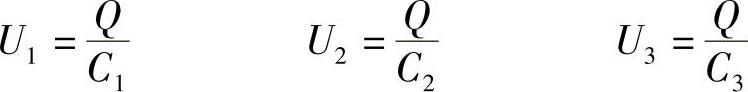
根据基尔霍夫第二定律，列回路电压方程

U=U₁+U₂+U₃ （3-5）

对等效总电容C而言，它两端的电压是U，所带电荷量是Q，应有关系式U=Q/C，代入式（3-5）得

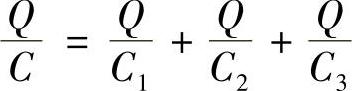
即

电容器串联时，总电容的倒数是各只电容器电容的倒数之和，总电容C比每只电容器的电容都小。这相当于加大了电容器两极板间的距离d，因而电容减小，如图3-10所示。(www.xing528.com)

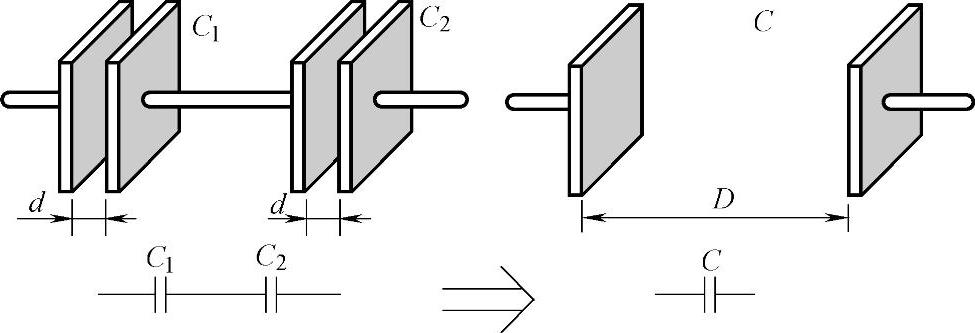
图3-10 串联电容器组的电容量

电容器串联时的各电容间关系，与电阻器并联时的各电阻间关系相似。当有n只电容器串联时，可推广为

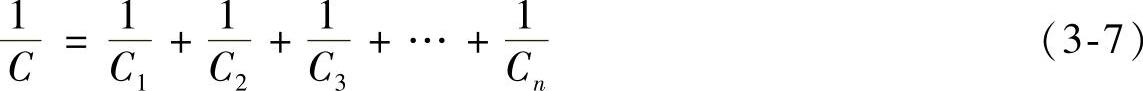
当n只电容器的电容相等，均为C₀时，总电容C为

【例3-4】有三只电容器，C₁=2μF，C₂=3μF，C₃=6μF，若将它们串联起来后，接到60V的电压上，求每只电容器承受的电压U₁、U₂、U₃是多少？

解：由电容器串联的公式（3-6）求出总电容C

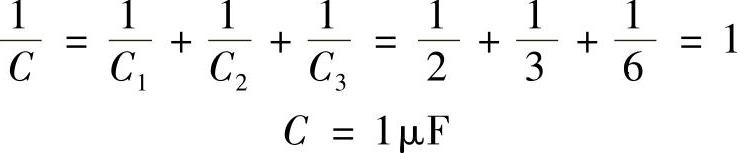
根据总电容、总电压和总电荷量的关系，可求出总电荷量Q

Q=CU=1×10^-6×60C=60×10^-6C

电容器串联电路中，各个电容器所带电荷量相等，即

Q=Q₁=Q₂=Q₃=60×10^-6C

电容器C₁、C₂、C₃所承承受的电压分别为

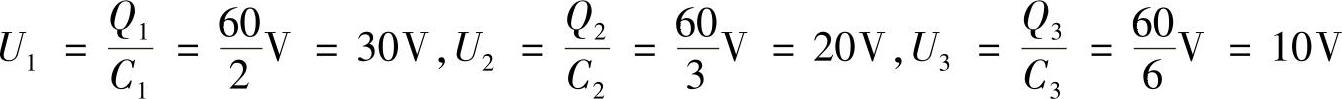
从此例题可以看出，在电容串联电路中，电容量大的电容器分配到的电压小；电容量小的电容器分配到的电压反而大，即在电容器串联电路中，各个电容器两端的电压与其自身的电容量成反比。

【例3-5】有两只电容器C₁和C₂，它们串联后两端接到360V的电压上，其中C₁=0.25μF，耐压为200V；C₂=0.5μF，耐压为300V。问电容器能否正常工作？

解：电容能否正常工作，要看电路中每只电容器上所承受的电压是否超过了自身的耐压。若在耐压范围之内，工作是安全的。

由已知条件可知，电路的总电容C为

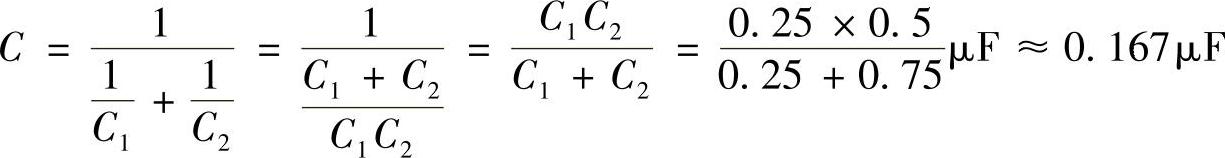
电容器C₁和C₁上所带电荷量相等，且等于总电荷量Q

Q=Q₁=Q₂=CU=0.167×10^-6×360C≈60×10^-6C

电容器C₁和C₁上承受的实际电压分别为

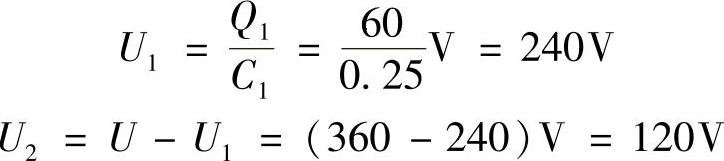
可见，电容器C₁实际所承受的电压超过了它的耐压（200V），所以C₁会被击穿，致使360V电压全部加到C₂上，也超过了C₂的耐压（300V），所以C₂也会被击穿。因此，这样使用电容器，电路是不安全的。