二元相互溶解的固相共存优化研究

相对于均匀的二元（或多元）单相液体，均匀的二元（或多元）单相的固体称为固溶体（solidsolu-tion）。

Solidsolution直接的意思是“固体溶液”，中文称“固溶体”很恰当。因为“固体溶液”和“溶液”根本是两回事。所谓“固溶体”，宏观上是一个均匀的单相合金，但却有它自己确定的晶体结构。而溶液总体上来说是在较高的温度下，组元A和B的原子借弥散力的引力和热扰动的作用而混匀为均匀的一个单相，不同的原子相混，基本是无序的。在固态下，除了玻璃态的固体才算真正的固体溶液以外，固溶体不可能像溶液那样无序混溶。晶体物质都有自己特有的结晶格子，有保护自己结晶格子不被破坏的势垒。另一个组元A如果想“溶”进B的格子里去形成均匀的固溶体，只有两种可能：一种是A原子的体积相对于B的结晶格子的空隙来说极小极小，能够钻进B的格子空隙中去，形成部分的所谓间隙固溶体（inter-stitialsolidsolution），关于这部分不在本书讨论的范围以内；另一种就是用A原子取代原来组元B结晶格子点上的B原子，并且保持原有B的晶格不变，或者用B原子取代原来组元A结晶格子点上的A原子，并且保持原有A的晶格不变，形成一种格子点上被两种组元的原子混合占据的状态。如果希望从A一直均匀取代到B，或者是从B一直均匀取代到A，就必须满足一些条件，例如：A和B具有相同，至少极为接近的结晶格子类型；A和B的原子半径（也就是原子体积大小）相近；A和B的化学性质相近（否则二者会起化学反应，生成化合物）等。两个组元完全“固溶”叫做生成了连续固溶体（continuoussolidsolu-tion）。组元间生成这样固溶体的体系，在元素周期表上大半都是处在上下、左右相近的位置的两个元素。如：AgAu、CuNi、GeSi、FeNi、MoW等。相图中的“（A，B）”，是一种通用的表示组元A和组元B生成的连续固溶体的符号。

图3.5所示是组元A和B之间生成连续固溶体的三种类型。图3.5a表示生成的是均匀的连续固溶体，ls连线是结线，表示平衡着的液相和固溶体相的温度和组成。图3.5b和图3.5c分别是具有最低点和最高点熔化温度的固溶体。

对图3.5a的第一种固溶体而言，显然组成这类固溶体的两个组元的条件最为“匹配”，这类相图（如同族紧邻的AgAu、SiGe、MoW、PdPt以及同周期紧邻的CuNi、PdRh等相图）常可见到。液相限和固相限间的距离宽度往往反映两个组元匹配的程度。匹配得越好，宽度越窄。一些稀土元素之间，例如HoEr等形成的连续固溶体的宽度几乎为0，所以看到这类固溶体相图只有一条线时，不要有所误解。

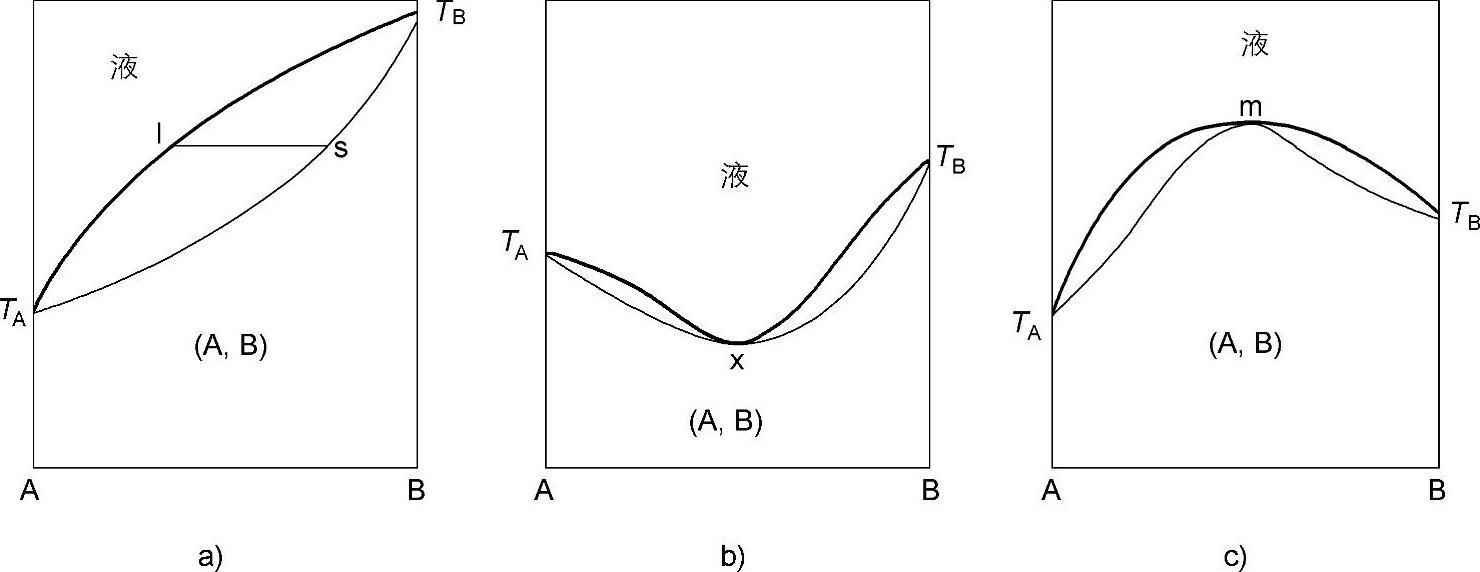
图3.5 生成连续固溶体二元系的三种类型

在生成各种连续固溶体的条件中，两个组元在一定的温度范围内必须具有同一类型的结晶格子，这是绝对必要的条件。那些虽处于周期表同族，但两个组元的原子体积相差稍大，或者不同族但在周期表上处于紧邻位置的两个组元，其原子体积和化学性质都稍有差异的，虽然结晶格子相同，但这时形成的连续固溶体往往具有液相限的最低点，如图3.5b所示。说明组元之间匹配稍差，有共晶结晶的趋势。这类例子屡见于同族的CsK、NiPd、AuCu、AsSb、BaCa系以及不同族但在周期表中位置紧邻的CrV、CoPd等体系中。(www.xing528.com)

图3.5c所示为具有最高点温度的连续固溶体。如果有这种类型的连续固溶体的出现，说明组元之间有生成新化合物的趋势。新的中间化合物总是会产生自己特殊的结晶格子，这就会和两个组元的结晶格子产生“失配”难于互溶，在这种情况下往往就会产生化合物。事实上，这种具有最高点的，理论上存在的固溶体，除了在同一个有机化合物的两个旋光异构体之间能够出现这一特殊例子之外（例如左旋和右旋香芹肟之间），在现有由纯组元构成的二元系的相图中根本就找不到实例。

在图3.5b或图3.5c中的最低点或最高点的自由度可以由吉布斯相律算出：

F（自由度）=2（组元数）+1（恒压时）-2（相数）=1

因此组成有一定的可变范围，固相限和液相限两条曲线在此处是相切的。那种表达成自由度为0的相图画法是不正确的，如图3.6所示。因为按照图中的x点或m点的画法，属于一种“奇点”（singularpoint），它的温度和组成都是不能变的，也就是自由度为0，显然和相律计算的结果矛盾。再有如图3.6a所示，两条液相限曲线在x点冷却，呈共晶析出，而温度降低至固相时却又能连续互溶，这也是完全不合理的。至于在图3.6b中的m点违反相律已如上述，但如果认定m点是一个组成确定而又是稳定的化合物，并通过m点向下作一条垂线和组成坐标相交，此时将这条垂线当作一个“赝组元”并作赝单元系来处理，那么修改后的相图就可以勉强不违背相律，但是这种实例正如前述，根本就找不到。

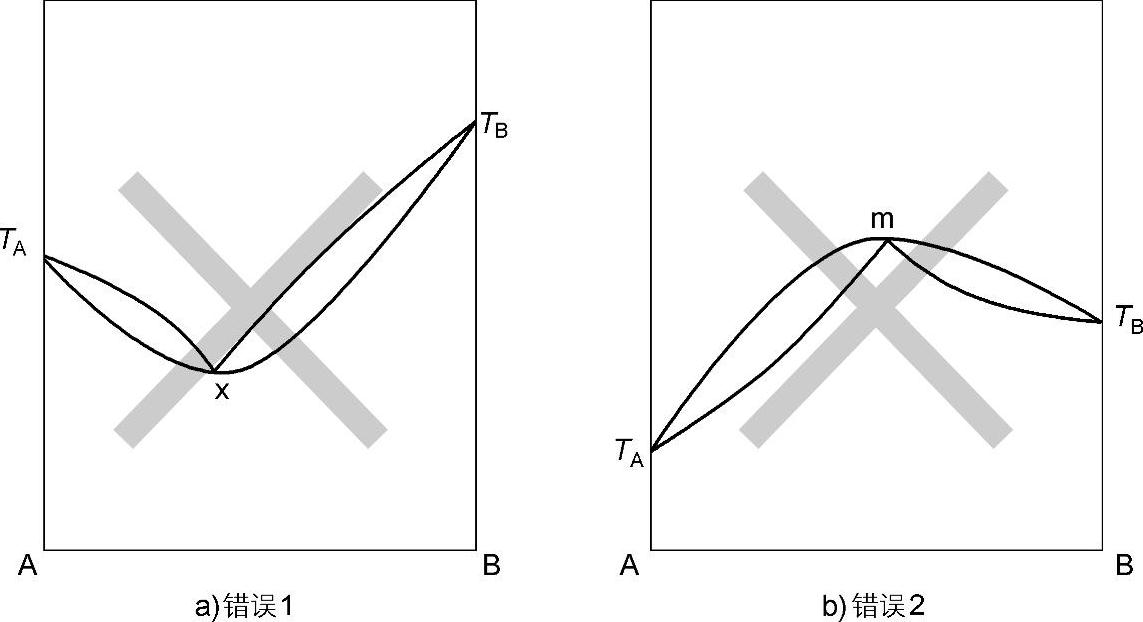
图3.6 两种连续固溶体相图的不正确表达