探析风电的广域平滑特性

风电场一般由几十台甚至几百台风力发电机组组成，由于风电场（特别是大型风电场）占地面积很大，必然涉及同一风电场内机组地理分布的问题，也就是说，由于风速分布不同和相邻风为电机组间的尾流效应等，导致同一时刻、同一阵风引起的不同地理分布的风力发电机组的风况不一致。由于风电场的这种空间特性，风电场中风力发电机组的运行工况各不相同，使整个风电场的功率波动幅度和频率相对单台风力发电机而言大大减少，因此大型风电场往往显示出相对于单台风力发电机较好的输出功率特性，风电场的这种特性称为广域自平滑作用或集群效应。

广域自平滑特性在大规模风电并网应用中是不得忽略的重要特性之一，尤其在风储联合应用的容量配置过程中，应充分考虑风电场的广域自平滑作用。然而，无论以单台风力发电机为单位配置储能，还是以整个风储为单位配置储能都不是最优方案，风力发电机组的合理分组，将有助于提高自平滑特性在风储联合应用中发挥作用。基于风电场的有功功率数据，通过分析风力发电机群的广域自平滑作用，得到合理分组的相关依据。

首先分析装机容量与风力发电机群的广域自平滑作用的关系，通过分析不同台数的风力发电机群的风电出力波动和平均出力，研究装机容量与风力发电机群平滑作用的关系。

仍以辽宁百兆瓦级风电场为例，该风电场共有66风力发电机组，全部并网运行。对比采样时间间隔为15min时该风电场5台、10台、15台、20台、25台、30台、35台、40台、45台、50台、55台、60台、65台风力发电机的累加输出的波动率，分析风力发电机群的波动率与装机容量的关系，研究装机容量与风力发电机群平滑作用的关系。

图2-10是15min前后不同台数的风力发电机群的波动率随装机容量变化的概率密度分布图。为便于观察分析结果，作出图2-10的俯视图，如图2-11所示。

图2-10中波动率随装机容量的增加越来越集中的分布在波动率较小范围内，从图2-11可以更明显地看出这种趋势，随着装机容量的增大，图中央的颜色逐渐加深，即表示波动率分布在这个范围内的密度逐渐增大。也就是说，随装机容量的增加，波动率的分布越来越收敛，这说明风力发电机群自身具有互补平滑作用，并且随着风力发电机群装机容量的增加，自平滑作用增强，这也验证了大型风电场具有相对较好的输出功率特性这一说法。因此对风能资源的集中开发，建设大规模风电场甚至风电基地不仅具有明显的规模经济优势，还能够有效降低风电出力波动率，有利于缓解电力系统的调峰调频的矛盾。

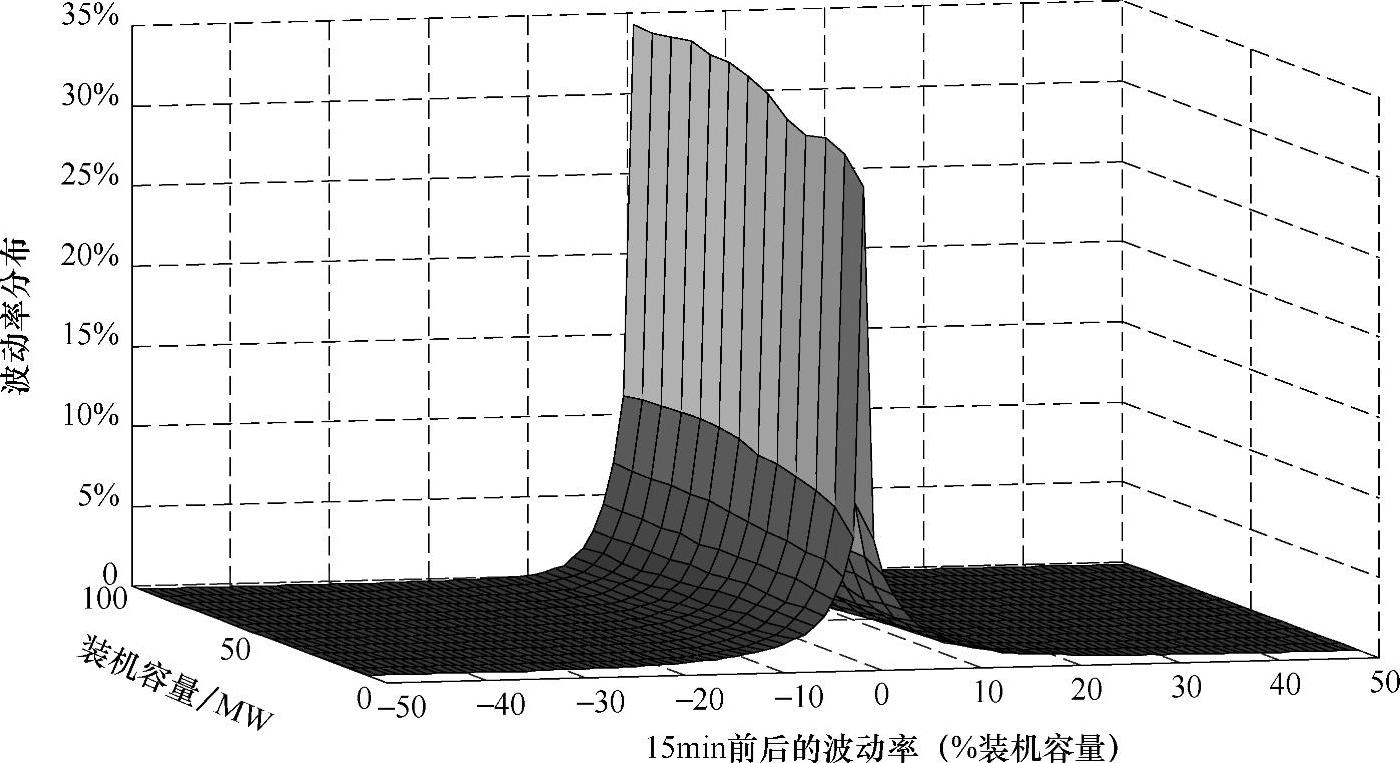
图2-10 装机容量与波动率的概率分布关系

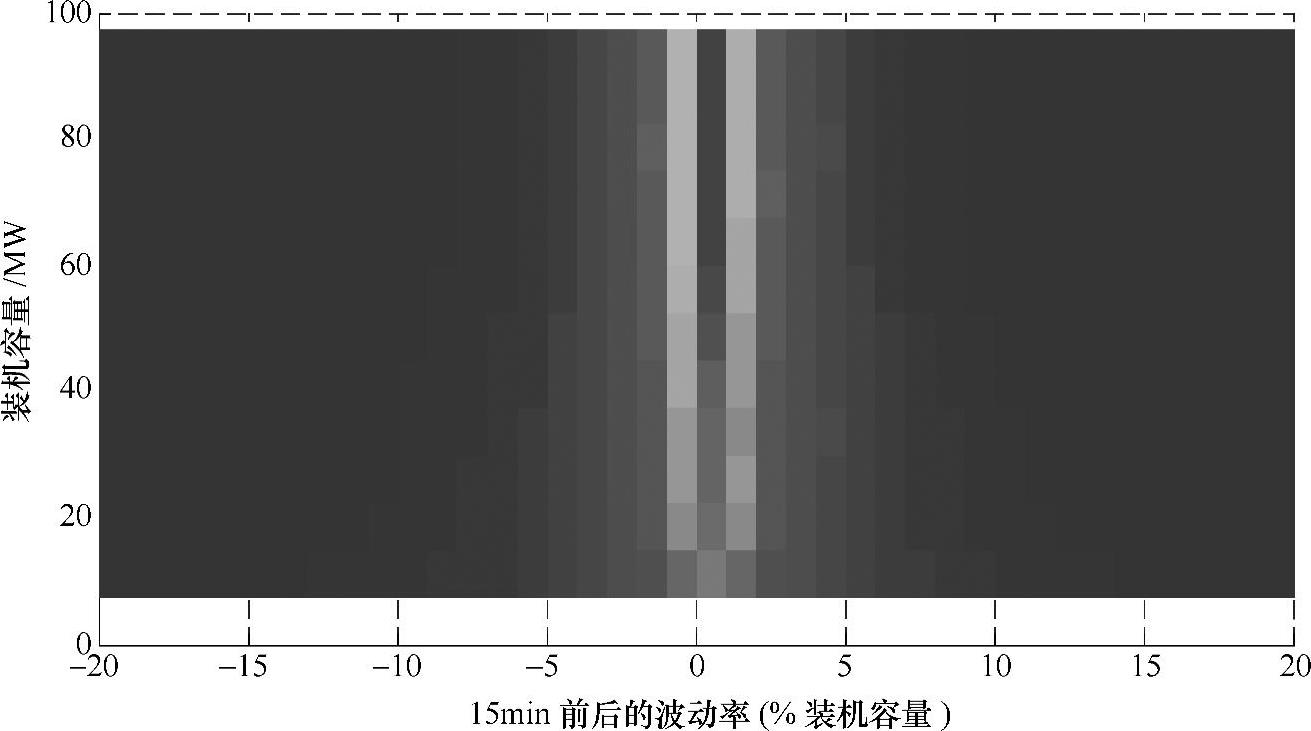
图2-11 装机容量与波动率的关系

图2-12和图2-13为风电场的5台、65台风力发电机的平均出力15min前后的分布情况，通过分析风力发电机的平均出力的波动与装机容量的关系，研究装机容量与风力发电机群平滑作用的关系。

对比图2-12和图2-13，可以看出65台风力发电机15min前后的平均出力明显更集中分布在图的对角线周围，说明65台风力发电机的平均出力在15min前后波动较5台风力小，说明65台风力发电机出力的波动小于5台风力发电机出力的波动。

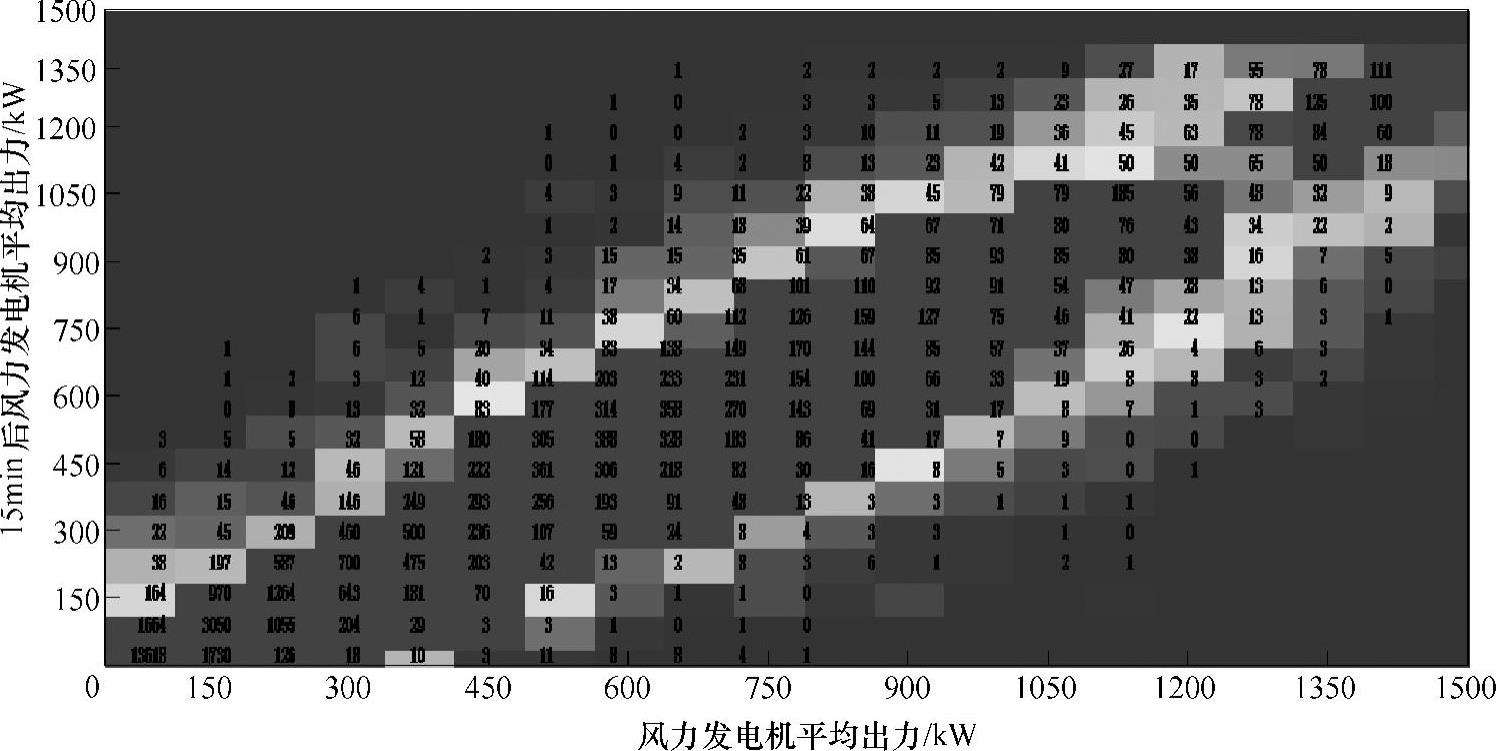
图2-12 15min前后5台风力发电机的平均出力分布

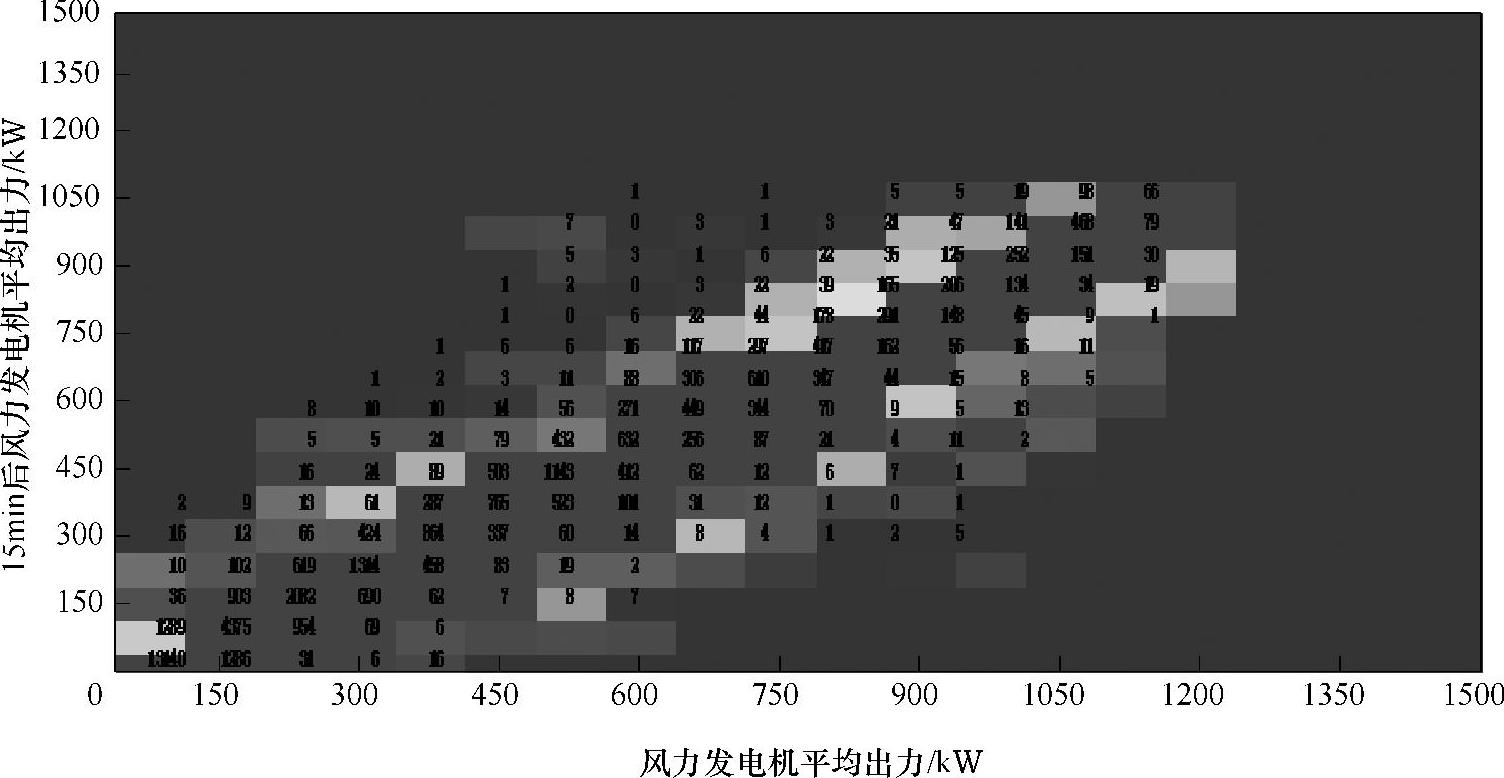
图2-13 15min前后65台风力发电机的平均出力分布

在风力发电机群的广域自平滑作用随装机容量增加而增强的结论基础上，进一步分析风力发电机的地理分布和连接结构与风力发电机群平滑作用的关系。风力发电机群中风力发电机的地理分布使得不同风力发电机风速到达高峰和低谷的时间不同，不同风力发电机的出力最大和最小值出现时刻也不同，从而降低了风力发电机群整体的出力波动。该百兆瓦级风电场的66台风力发电机的连接结构如图2-14所示。

对比分析单台风力发电机、单线（17台）风力发电机和整个风场（66台）的风力发电机总出力和总出力波动率，如图2-15所示。从图中可以看出单线风力发电机有功输出曲线比单台风力发电机的曲线平滑，整个风场的有功输出曲线比单线风力发电机的曲线平滑，但是曲线的平滑程度不及从单台风力发电机到线的变化显著。(www.xing528.com)

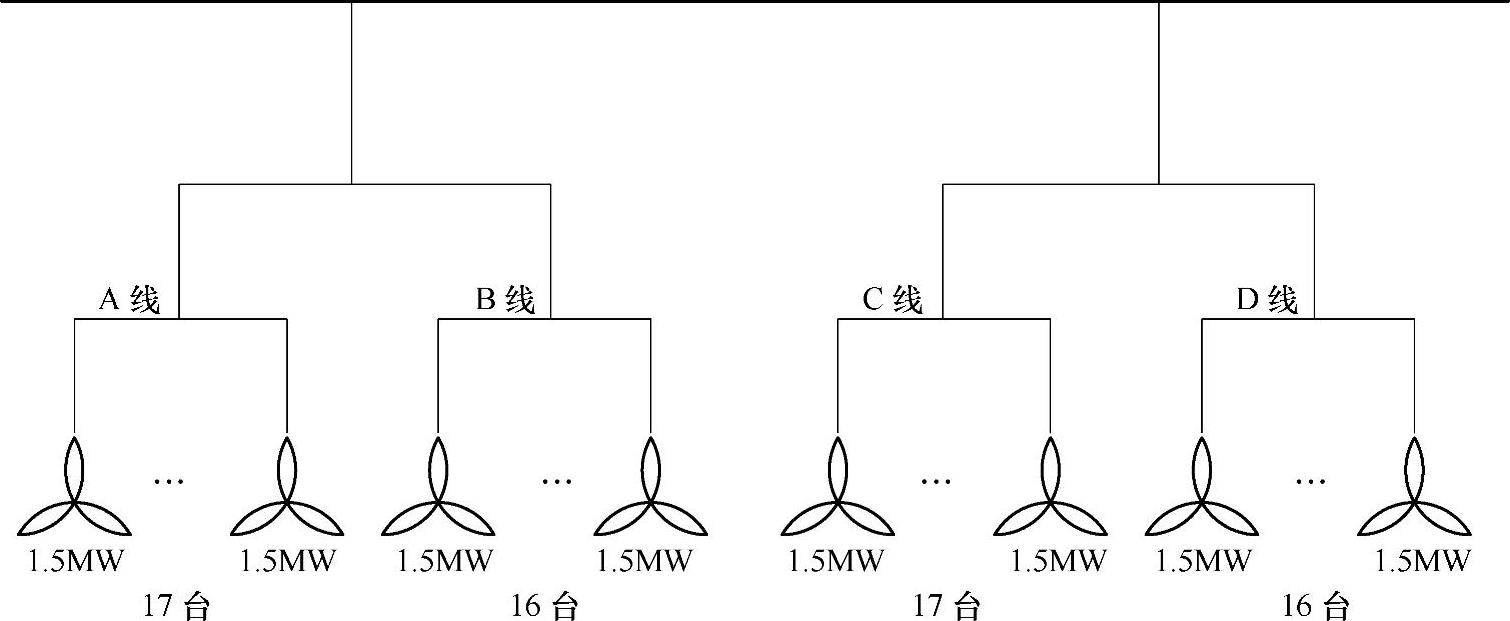
图2-14 风电场接线示意

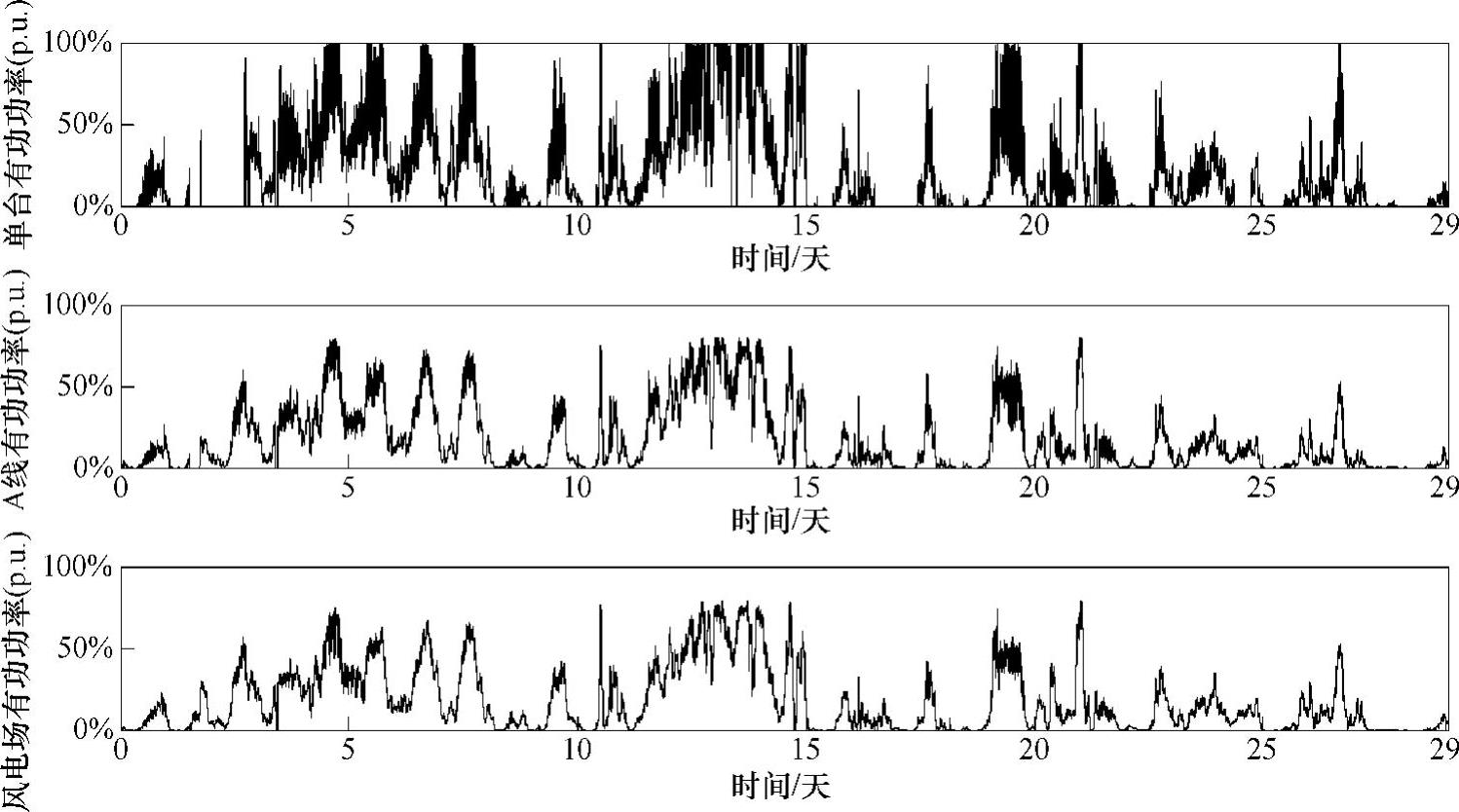
图2-15 风电场单台风力发电机、A线风力发电机、整个风场风力发电机的输出有功功率

图2-16～图2-18对比风电场的单台风力发电机、单线（17台）风力发电机和整个风场（66台）的输出有功功率在时间间隔为1min时的波动率曲线，通过对比效果可以看出单线风力发电机的波动率明显小于单台风力发电机的波动率，风场的波动率小于单线风力发电机的波动率，但效果并不明显。

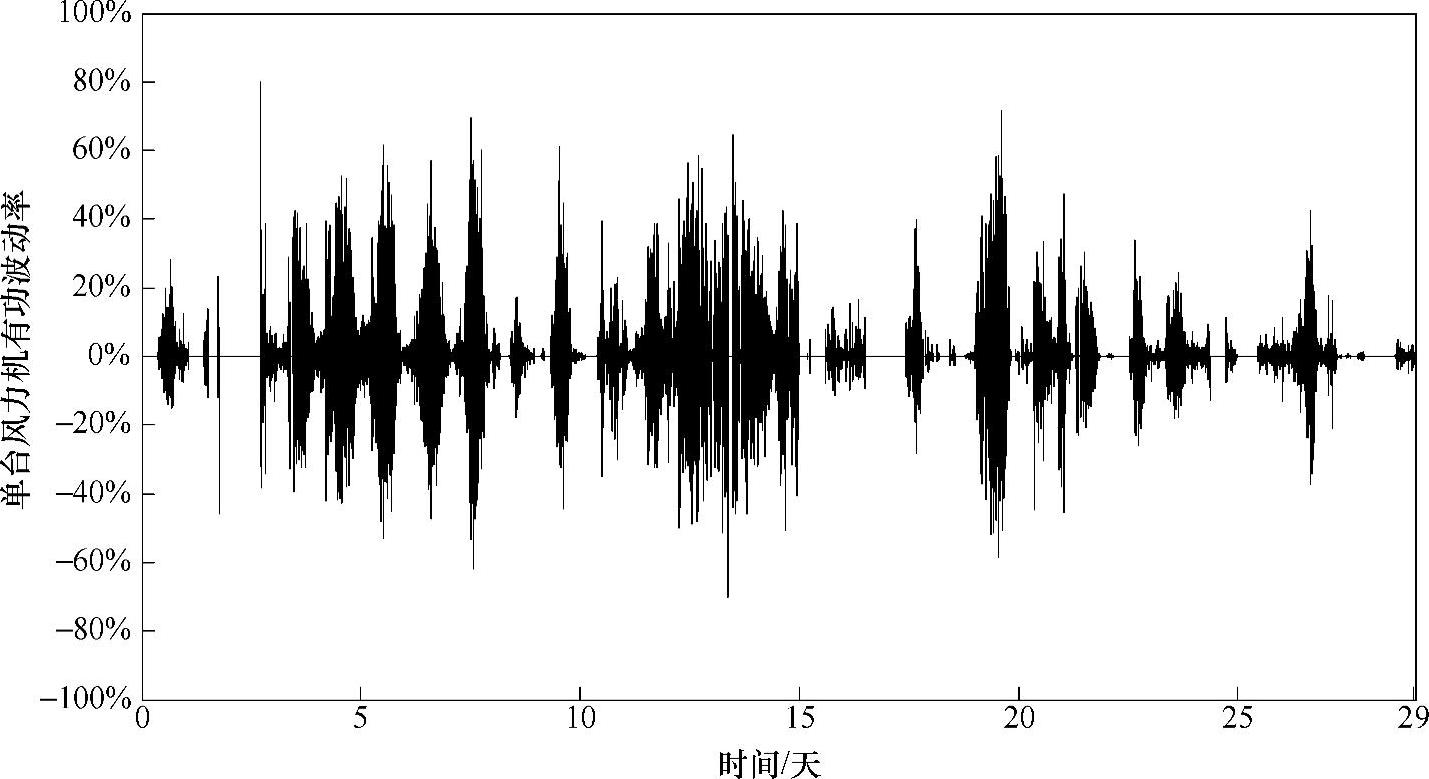
图2-16 单台风力发电机的功率波动率曲线

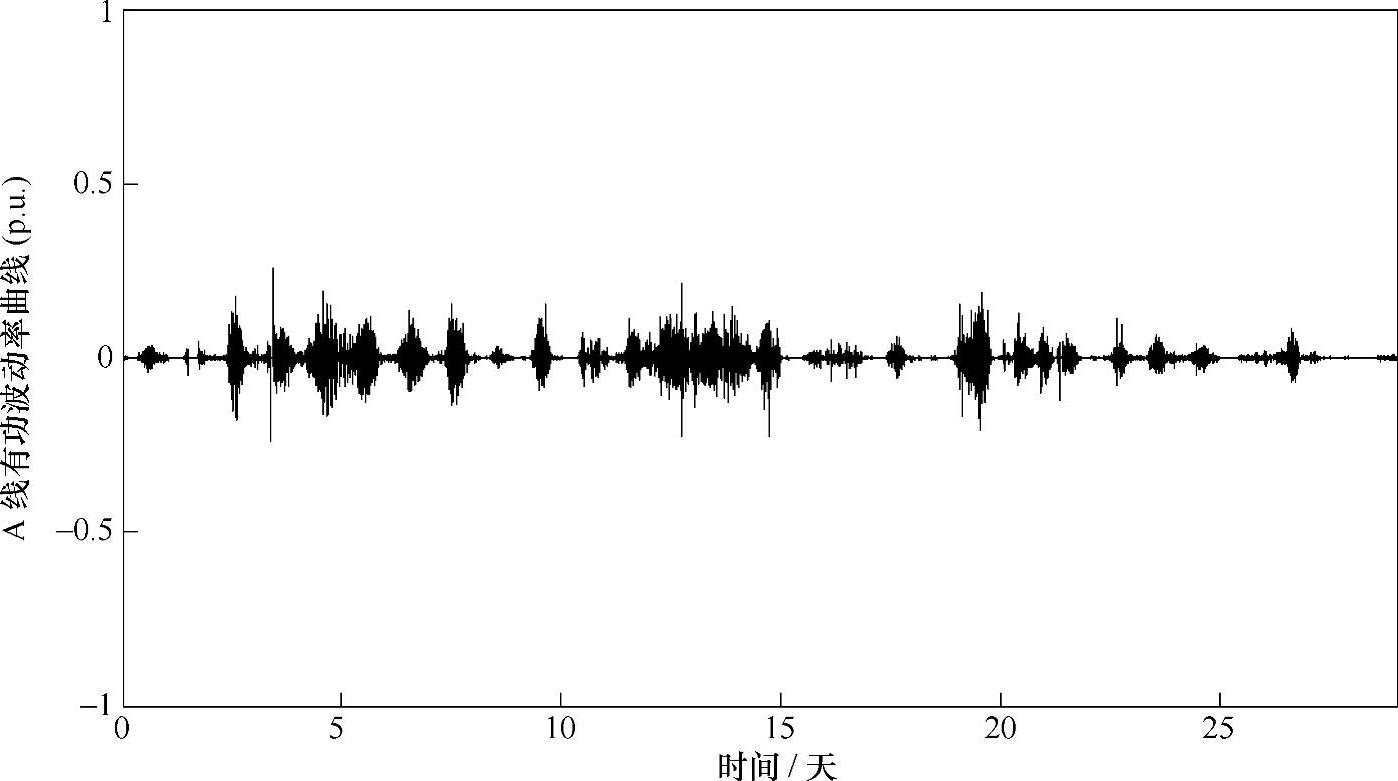
图2-17 A线风力发电机的功率波动率曲线

从单台风力发电机到单线的17或16台风力发电机，有功输出曲线和输出波动率曲线都变化较大，说明风力发电机群有较强的平滑特性。在考虑风力发电机群的集群效应的基础上以风力发电机群为单位配置储能，相较于以单台机组为单位配置储能，可以节约储能容量，从单线的17台风力发电机再增加到整个风场的66台风力发电机，两个方面的变化都不明显。为了观察随着风力发电机台数逐台增加，风力发电机群出力的最大波动率的变化趋势，排除偶然的大功率波动对分析结果造成影响，波动率的置信区间设为99.9%。图2-19为在置信区间为99.9%时不同风力发电机台数的风力发电机群的最大波动率曲线，从图中可看出随着风力发电机台数逐台增加，风力发电机群的最大波动率开始下降明显，到10台时开始变缓，增至17台时变化趋于平稳，增至整个风电场相较于17台的风力发电机群最大波动率变化很小。这说明风力发电机群的平滑特性不仅与风力发电机群的装机容量（风力发电机台数）相关，还与风力发电机的地理分布和连接结构有关。

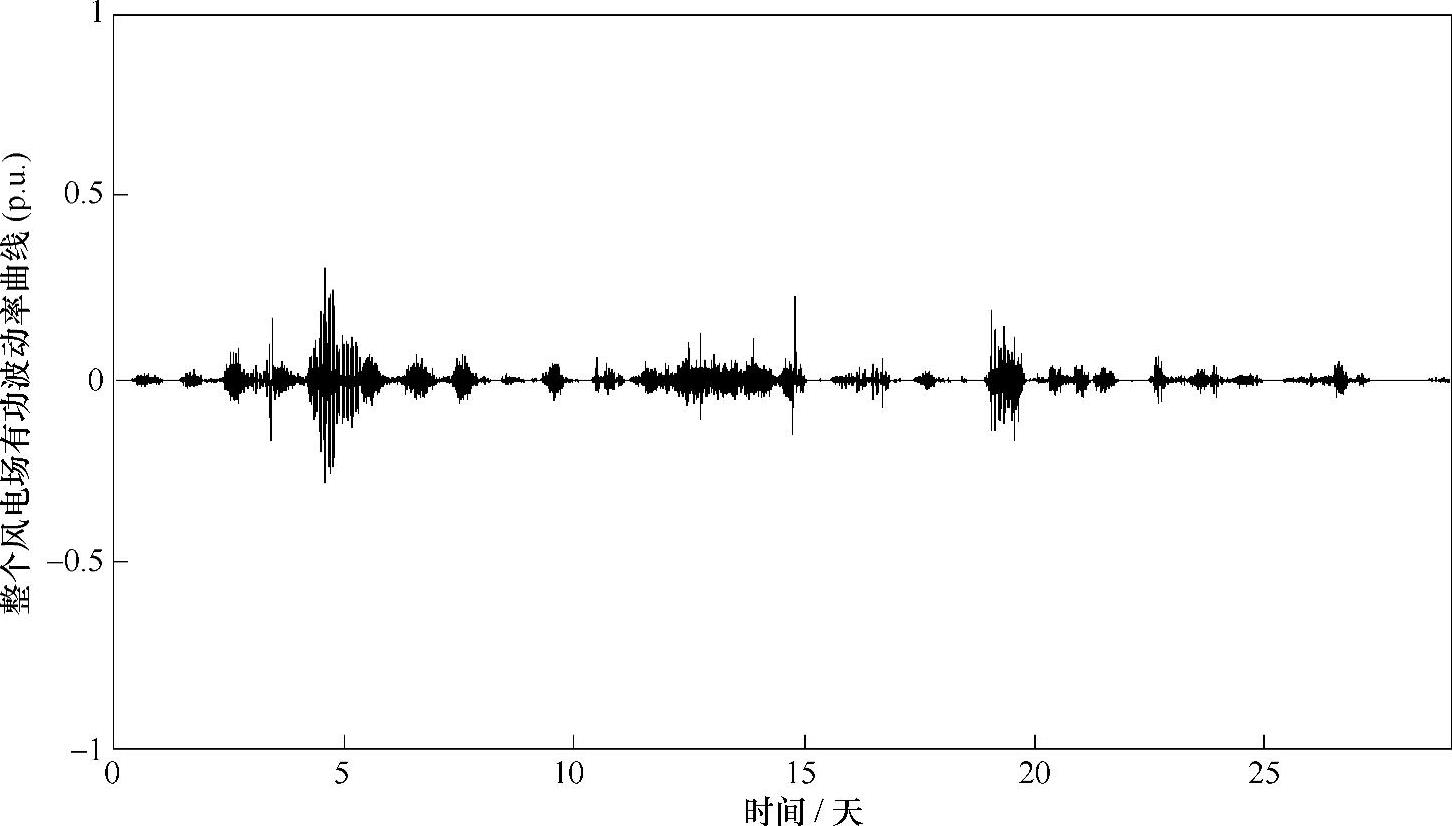
图2-18 整个风场的功率波动率曲线

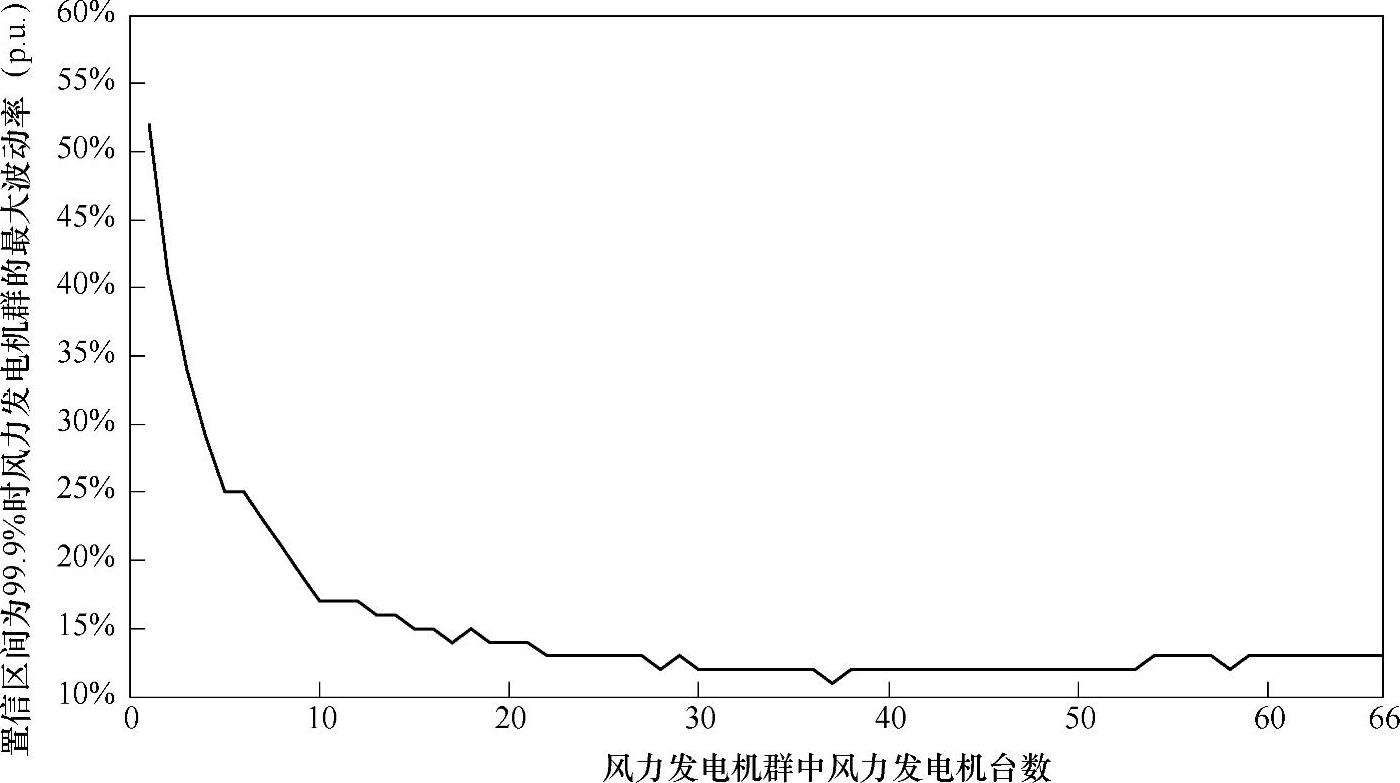
图2-19 风力发电机台数与风力发电机群最大波动率的关系曲线

考虑配置储能平滑风电出力波动时，在考虑风力发电机群自身的广域平滑的基础上，以风力发电机群甚至整个风电场为单位集中配置储能相较于单台风力发电机组分别配置可以降低总体储能容量，节约储能成本。

风力发电机组输出功率经交流传输线路至电网时，输电线路和变压器在运行时产生的功率损耗会随着风电功率的波动而波动，风力发电机组配置储能后平滑了风电功率波动，从而减少线路的功率损耗。

综合考虑节约储能成本和减少线路的功率损耗，采用储能系统平滑风电场风电功率波动时，简单地以单台机组，或者整个风电场规模进行储能配比都不符合科学规划的原则。根据研究分析应以17台风力发电机组成的风力发电机群为单位配置储能，同时考虑风电场风力发电机组的地理分布、连接结构，将可较充分地发挥风力发电机群的广域自平滑作用。建议今后规划建设配置储能的风电场时，考虑为风力发电机群配置的储能系统的接入方式。