已往水库冲淤计算中采用由输沙平衡原理建立的有限差分法，是假定各断面的实际含沙量和水流的挟沙能力相等，忽略冲淤过程中含沙量的变化需要一定的时间和一定的流程。然而实际情况并非如此。长江科学院于20世纪70年代基于冲淤过程中断面实际含沙量存在调整过程的不平衡输沙原理，建立了水库冲淤的计算方法。该方法具有如下主要特点：一是考虑到悬移质泥沙冲淤过程中，每一断面的含沙量不一定等于其水流挟沙力；二是随着含沙量的沿程变化，悬移质颗粒级配和床沙颗粒级配沿程也相应发生改变。这种计算方法，只限于悬移质冲淤计算，不包括推移质冲淤情况。
（一）模型的基本方程组
1.水流的运动方程和连续方程
经用实测资料反算，β取值为：沉沙条渠、河道型水库和天然河道采用0.75；湖泊型水库和胃状放淤区采用0.50。
（2）冲刷过程悬移质粒配的变化。假定冲刷过程中，河段进口断面进入的悬移质粒配在计算时段和河段内是不变的，则出口断面的悬移质粒配应由进口断面的悬移质粒配与补给的床沙粒配相加。
式中：Q为流量；H为水位；A为断面过水面积；t为时间；g为重力加速度；Jf为能坡。
2.悬移质平均含沙量的沿程变化
二维、恒定、非均匀流条件下的泥沙紊动扩散方程式为：
式中：x、z为纵向和垂向坐标的量；vx、vz为x及z向的流速分量时均值；S为时均含沙量；ω为泥沙沉降速度；εz为沿z向的泥沙紊动扩散系数。
将式（3-14）各项乘以dz，并由z=0到z=h之间积分。假定河底向上紊动扩散的泥沙数量εz
|z=h，只与当时的水力条件有关，而不依赖于河底含沙量Sb，则可以用冲淤平衡情况下的底部下沉泥沙数量ωS*b来代替，其中S*b为河底水流挟沙能力。因单宽流量q沿程不变，则得：
假定河底含沙量Sb和河底水流挟沙力S*b与断面平均含沙量S和断面水流挟沙力S*的比值相等，其值为a，称为恢复饱和系数；则一维、恒定、非均匀流断面平均含沙量沿程变化的基本方程式为：
式中：S0，S*0为河段进口断面的含沙量和水流挟沙力；S，S*为河段出口断面的含沙量和水流挟沙力；L为河段长度，利用实测资料反求α值，淤积时为0.25，冲刷时为1.0。
对于非均匀沙，假定分粒径组泥沙含沙量沿程变化仍可用均匀沙方程式表达，即：
式中：i=1，2，3，…，n。
根据各粒径组泥沙量百分比Pi，有Si=PiS，S*i=PiS*。
将式（3-17）对i求和，即可得非均匀沙断面平均总含沙量的沿程变化方程式：
式中：λ*为冲刷厚度Δh和冲刷扰动厚度的比值。
式中：P0i，Pi为河段进、出口断面第i粒径组泥沙重量百分比；S*0，S*为河段进、出口断面非均匀沙的水流挟沙力。
非均匀沙水流挟沙力公式采用以下形式：
3.悬移质粒配的沿程变化
（1）淤积过程悬移质粒配的变化。计算河段进出口断面悬移质i粒径组泥沙重量百分比分别为：
对各组粒径求和，得：
式中：ω中为床沙平均沉速的中值，由式（3-25）确定。
4.床沙粒配的变化
（1）淤积过程床沙粒配的变化。在淤积过程中，床沙粒配即为淤积物粒配。所以淤积后床沙i粒径组重量百分比Ri为：
经用实测资料反算，β取值为：沉沙条渠、河道型水库和天然河道采用0.75；湖泊型水库和胃状放淤区采用0.50。
（2）冲刷过程悬移质粒配的变化。假定冲刷过程中，河段进口断面进入的悬移质粒配在计算时段和河段内是不变的，则出口断面的悬移质粒配应由进口断面的悬移质粒配与补给的床沙粒配相加。
式中：λ*为冲刷厚度Δh和冲刷扰动厚度的比值。
将式（3-21）代入，即得：
式中：ω中为床沙平均沉速的中值，由式（3-25）确定。
4.床沙粒配的变化
（1）淤积过程床沙粒配的变化。在淤积过程中，床沙粒配即为淤积物粒配。所以淤积后床沙i粒径组重量百分比Ri为：
将式（3-21）代入，即得：
（2）冲刷过程床沙粒配的变化。在冲刷过程中，床沙粒配变化计算式为：
（2）冲刷过程床沙粒配的变化。在冲刷过程中，床沙粒配变化计算式为：(www.xing528.com)
式中：ω中由式（3-25）确定。
式中：ω中由式（3-25）确定。
5.悬移质河床的变形方程
5.悬移质河床的变形方程
式中：Z为水位；Q为流量；A为过水面积；S为断面平均含沙量；γ为淤积物干容重；ΔA为冲淤面积；x为沿程距离；t为时间。
（二）基本方程组的简化
由于所研究的问题是长时段、长河段内发生的冲刷，在实际计算时对基本方程组进行了简化，将整个计算时段划分成若干个小的计算时段，将长河段划分为若干个短河段，且在计算时段内和河段内除ΔA以外，其他因子不变，即按恒定流考虑，而在不同时段不同河段各因子可以不同。
经差分方程变换、整理得如下应用方程。
1.水面线的计算式
式中：Z为水位；Q为流量；A为过水面积；S为断面平均含沙量；γ为淤积物干容重；ΔA为冲淤面积；x为沿程距离；t为时间。
（二）基本方程组的简化
由于所研究的问题是长时段、长河段内发生的冲刷，在实际计算时对基本方程组进行了简化，将整个计算时段划分成若干个小的计算时段，将长河段划分为若干个短河段，且在计算时段内和河段内除ΔA以外，其他因子不变，即按恒定流考虑，而在不同时段不同河段各因子可以不同。
经差分方程变换、整理得如下应用方程。
1.水面线的计算式
2.悬移质含沙量的变化
2.悬移质含沙量的变化
其中：
其中：
3.淤积时的悬移质级配
3.淤积时的悬移质级配
4.淤积时的淤积物级配
4.淤积时的淤积物级配
5.冲刷时的悬移质级配
5.冲刷时的悬移质级配
6.冲刷后的河床剩余淤积物级配
6.冲刷后的河床剩余淤积物级配
7.冲淤引起的河床变形
7.冲淤引起的河床变形
式中：Δt为时段；Δx为两断面间距；S、S*分别为含沙量及挟沙力；λ为淤积百分数；λ*为槽中被冲走的各层百分数；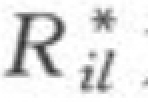
为平均级配；
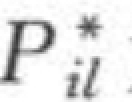为河床冲起的级配；
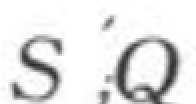为槽中各层淤积物的补给输沙率；“0”脚标为已知断面；“L”脚标为淤积物层数（L=1，2，…，n）；“i”脚标为悬移质颗粒分组数（i=1，2，…，n）。
8.断面特性曲线的处理
宽阔断面淤积时沿湿周等厚分布，冲刷时仅冲槽不冲滩；窄深断面均按水平状态淤积或冲刷。
式中：Δt为时段；Δx为两断面间距；S、S*分别为含沙量及挟沙力；λ为淤积百分数；λ*为槽中被冲走的各层百分数；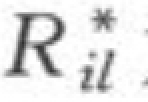
为平均级配；
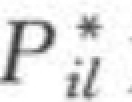为河床冲起的级配；
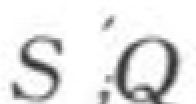为槽中各层淤积物的补给输沙率；“0”脚标为已知断面；“L”脚标为淤积物层数（L=1，2，…，n）；“i”脚标为悬移质颗粒分组数（i=1，2，…，n）。
8.断面特性曲线的处理
宽阔断面淤积时沿湿周等厚分布，冲刷时仅冲槽不冲滩；窄深断面均按水平状态淤积或冲刷。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
