电力架空光缆的设计计算方法

架空光缆在使用过程中会受到自重、大风、覆冰和环境温度变化等的作用，使线缆的受力产生影响，在设计过程中，需要考虑各种恶劣气候条件下光缆的安全及寿命。

架空光缆的受力大小可依据悬链线公式进行近似计算。但悬链线公式中包含双曲线函数，计算比较复杂，故一般工程设计与施工常采用平抛物线公式，即线缆趋于拉紧，使应力偏大。根据经验，两种方程计算的结果误差实际上非常小，特别是弧垂系数小于10%时，应力增加还不到2%，因而可以忽略计算方面的影响，下面就按照抛物线公式进行计算。

抛物线公式分为斜抛物线公式和平抛物线公式两种。斜抛物线公式近似认为光缆重量沿悬挂点连线上均匀分布来进行简化，平抛物线公式则是近似认为光缆重量沿悬挂点间的水平线上均匀分布而简化得来。

假设气候条件变化时，即温度、风速、覆冰等引起光缆应力和弧垂随之改变，在计算某一气象条件下的线缆应力、比载及其他待求参数时，不考虑该气象条件所引起的线缆弹性伸长，也就是以档距内原始长度不变的原则，计算出待求气象条件下的线缆应力、比载及其他参数。为了便于计算，这里引用了比载的概念，即线缆单位长度、单位面积（单位体积）上的荷载，以N／m·mm2或MPa／m为单位。

（1）当原点O点位于光缆最低点时（图5.1.1）

简化的斜抛物线曲线方程为：

简化的平抛物线曲线方程为：

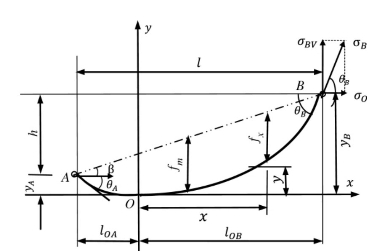
图5.1.1　坐标O点位于光缆最低点

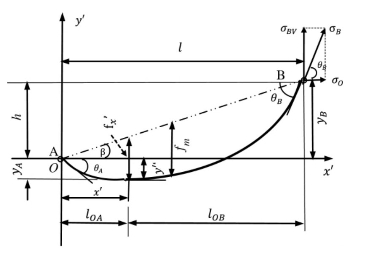
图5.1.2　坐标O点位于光缆悬挂点A

（2）当坐标O点位于光缆悬挂点A时（图5.1.2）

其简化的斜抛物线曲线方程为：

简化的平抛物线曲线方程为：

式中：l——档距（即两悬挂点之间的水平距离）（m）；

h——高差（即两悬挂点之间的垂直距离）（m）；

β——高差角，；

x，x′——光缆各点到纵坐标轴的水平距离（m）；

y，y′——光缆各点到横坐标轴的垂直高度（m）；

σ0——光缆各点的水平应力（也是最低点的应力）（N／mm2）；

γ——光缆比载（即单位长度，单位面积上的荷载）（N／m·mm2）。

一般情况下，光缆在未受风力作用时，光缆平面与地表面垂直，两端只有垂直于地面的平面即光缆平面内的力。但是，大多时候光缆会受风的影响，形成风偏，如图5.1.3所示。

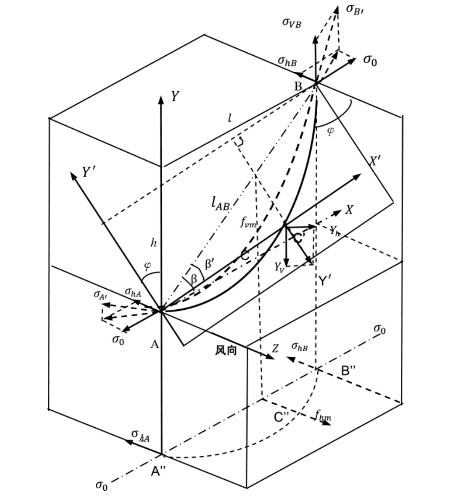
图5.1.3　风偏情况下光缆受力图

光缆风偏后，必然位于光缆自身质量、覆冰、风压等综合比载作用下所形成的平面内，称风偏平面。如风偏平面与无风时光缆平面夹角为φ，光缆应力可分为水平投影面和垂直投影面两个应力，光缆弧垂（两悬挂点连线上各点到光缆上的垂直距离）同样分水平投影面和垂直投影面的弧垂。

按简化的斜抛物线公式计算，垂直投影面内最大弧垂fvm和两端应力σvA、σvB分别为：

水平投影面内的最大弧垂fhm和两端应力σhA，σhB分别为：(www.xing528.com)

按简化的平抛物线公式计算，垂直投影面内最大弧垂hvm和两端应力σvA，σvB分别为：

其中：γv——垂直投影面内的比载（N／mm2·m）；

γh——水平投影面内的比载（N／mm2·m）；

l——档距（m）；

σ0——光缆最低点轴向应力（N／mm2），一般常以此作为已知条件；

β——两悬挂点间的高差角，一般β＝tan－1（h／l）；h为两悬挂点间沿荷载方向的高差，当右侧悬挂点高于左侧悬挂点时h为正值，反之为负值。

由于悬链线公式计算复杂，一般小档距线路的工程设计常采用平抛物线公式，即光缆偏于拉紧，使应力偏大；大档距的线路则建议采用斜抛物线公式比较合理。

根据向量计算，光缆风偏平面内最大综合弧垂f′m及两端最大综合应力σB′和σA′可根据下面公式计算：

（1）光缆最大综合弧垂f′m

它为档距中央自该点对应的悬挂点连线上沿综合比载γ′作用线方向到光缆间的距离；γ′为风偏平面内的参数，即综合风荷比载。

（2）综合应力

光缆风偏后任一点的轴向应力σ′x等于沿线路的水平应力分量σ0、垂直线路的水平风荷载引起的横向应力分量σhx及垂直应力σvx的向量和，即：

也就是：

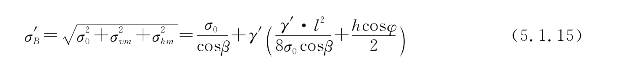
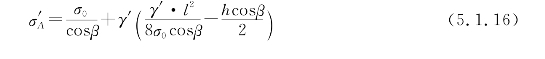
式中，φ为综合比载作用线与铅垂线间的夹角，

其中，γh为横向风荷比载，γv为垂直方向比载。

光缆两悬挂点A、B沿综合比载γ′作用方向上引起的应力分量σ′γA，σ′γB与σ0相垂直。其算式为：

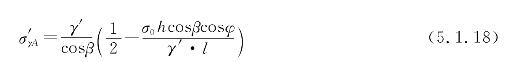
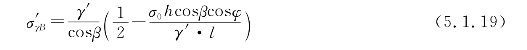
式（5.1.15）、式（5.1.16）中悬挂点轴向应力σ′B、σ′A的计算式也可由风偏平面内相互垂直的σ′0、σ′γB和σ′0、σ′γA分量的向量和求得。而在工程中常常需要将悬挂点的轴向应力分解为沿X、Y、Z方向的三个不在风偏平面的应力分量σ0，σc，σh。

以上计算公式中，当β＝0，即h＝0时，就是计算两端悬挂点等高时的弧垂和应力关系式。

最大弧垂：

受冰、风等作用时，其综合应力计算公式：