光纤通信的原理与应用

1.1.1.1　电磁波谱

光波是一种电磁波。依照波长（λ）的长短、频率以及波源的不同，电磁波谱可大致分为：无线电波、微波、红外线、可见光、紫外线、X射线和γ射线。

电磁波波谱如图1.1.1所示：

图1.1.1　电磁波波谱

无线电波波长从10－3m到3000m，一般的电视和无线电广播、手机等的波段就是用这种波。

微波波长从0.1cm到1m，这些波多用在雷达或其他通信系统。

光是原子或分子内的电子运动状态改变时所发出的电磁波。可见光，是人们能够直接感受而察觉的电磁波中极其狭窄的一个波段，它的波长范围很窄，在4000～7600Å（在光谱学中常采用埃（Å）作长度单位来表示波长，1Å＝10－10m）。从可见光向两边扩展，波长比它长的称为红外线，波长从7600Å到300μm；波长比可见光短的称为紫外线，它的波长为（10～380）×10－9m。

红外线的热效应特别显著。

紫外线则有显著的化学效应和荧光效应，这种波产生的原因和光波类似，常常在放电时发出。由于它的能量和一般化学反应所牵涉的能量大小相当，因此紫外光的化学效应最强。

红外线和紫外线都是人类看不见的，只能利用特殊的仪器来探测。无论是可见光、红外线或紫外线，它们都是由原子或分子等微观客体激发的。一方面由于超短波无线电技术的发展，无线电波的范围不断朝波长更短的方向发展；另一方面由于红外技术的发展，红外线的范围不断朝长波长的方向扩展。日前超短波和红外线的分界已不存在，其范围有一定的重叠。

伦琴射线，一般指X射线，这部分电磁波谱波长范围为（0.01～10）×10－9m。伦琴射线（X射线）是在能量相差悬殊的两个能级之间的跃迁而产生的粒子流。随着X射线技术的发展，它的波长范围也不断朝着两个方向扩展。在长波段已与紫外线有所重叠，短波段已进入γ射线领域。X射线具有很高的穿透本领，能透过许多对可见光不透明的物质。

γ射线是波长范围在10－14～10－10m的电磁波，这种不可见的电磁波是从原子核内发出来的，放射性物质或原子核反应中常有这种辐射伴随着发出。γ射线的穿透力很强，对生物的破坏力很大。

由于辐射强度随频率的减小而急剧下降，因此波长为几百千米的低频电磁波强度很弱，通常不为人们注意。实际中用的无线电波是从波长约几千米（频率为几百千赫）开始。波长50～3000m（频率100kHz～6MHz）的属于中波段；波长10～50m（频率6MHz～30MHz）的为短波；波长1cm～10m（频率30MHz～3×104MHz）甚至达到1mm（频率为3×105MHz）以下的为超短波（或微波）。有时按照波长的数量级大小也常出现米波，分米波，厘米波，毫米波等名称。中波和短波用于无线电广播和通信，微波用于电视和无线电定位技术（雷达）。

而光纤通信所用光波的波长范围为8000Å～2.0μm，属于电磁波谱中的近红外区。其所用波长区域与光纤综合特性有关，特别是衰减特性。

光在真空中的传播速度为3×108m／s，根据频率f、波长λ与光速c关系：f＝c／λ，计算出光纤通信用电磁波频率范围为1.5～3.75×1014Hz。

由于介质折射率比真空高，所以光线在介质中的传输速度v都比真空中的光速c低。

式中，n为介质折射率。

光线在大气中的速度接近于真空中的速度，所以n≈1。表1.1.1为常见的一些介质的折射率。

表1.1.1　常见物质的折射率和临界角

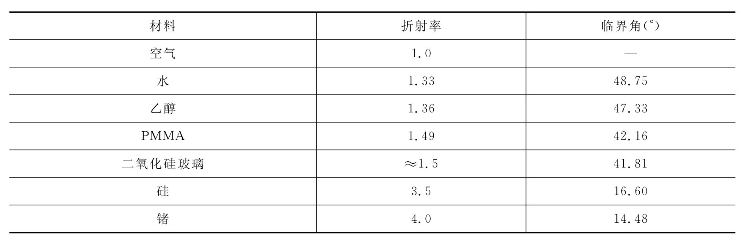
这些折射率并不是一成不变，受温度、波长等因素的影响，但也是非常接近真实值，仍然可以帮助我们做预测和计算。

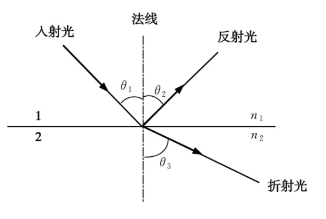
图1.1.2　平面介质波导光传播示意图

1.1.1.2　光传播理论、概念

在物理学上，光具有波粒二重性，既可以当成是光波，也可以当成是由光子组成的粒子流。因此，作为光波，它将遵从波动理论；作为粒子，又符合射线理论。

1）射线理论

按照射线理论，光在均匀介质中是以直线传播的，但在不同介质的分界面，存在折射和反射。

如图1.1.2所示，当光线从介质1（折射率n1）以θ1角射入介质2（折射率n2），且当n1＞n2时，将会有部分光线进入介质2，还有部分光线被反射回介质1。折射和反射光线的强度取决于两种介质的折射率。

根据Snell定律：

在n1＞n2时，逐步增大θ1，进入介质2的光线逐渐向界面靠近，当θ3接近于90°时，进入介质2的光线强度明显减少，甚至趋于零，此时反射光的强度接近于入射光的强度。

当θ3＝90°极限值时，入射光线所对应的角定义为临界角θc。所以临界角

当θ1≥θc时，入射光线将产生全反射。

因此，光在平面介质波导中传输时，当光线从折射率高的介质进入折射率低的介质，即n1＞n2，且入射角大于临界角时，在两种介质界面将会发生全反射。表1.1.1同时列出了几种常见物质的临界角。

全反射现象是光纤传输的基础。

射线光学理论指出，只要以大于临界角θc的任意角θ入射的光线都可以在光纤中传播。但是，如果考虑与射线相联系的平面波的相位在界面上的作用，仅有一些以大于θc的特定离散角度入射的波才可能沿光纤传播。下面用介质平板波导来模拟光纤光轴剖面进行分析。

如图1.1.3所示，假设一个平面波的两条光线1和2，以角度入射到界面上。根据平面波的性质，光线1和光线2在传播过程中等相面上的所有点相位必须相同。

光线1从A点到B点传播距离为s1，并在上下两个反射面发生两次相位突变δ，此时它的波前所经历的相位差应等于光线2从C点传播到D点且未经反射时波前所经历的相位差加上2kπ，即有n1ks1＋2δ＝2mπ＋n1ks1。由几何关系，容易得出AB的长度和CD的长度。波的相位变化包括因传播而引起的相移，也包括界面上产生反射时所引起的相位变化。

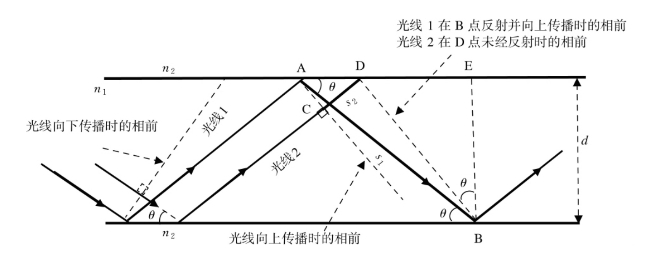
图1.1.3　光线在平面波导中传输波的相位变化

将s1和s2的值代入相位关系式并简化可以得到：

假如只考虑波的电场分量垂直于入射面的情况，那么因发射带来的相移为：

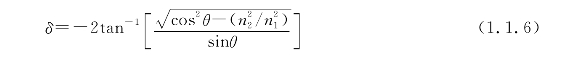
代入简化式中可以得到：

只有入射角θ满足该式的入射光才能在光纤中传播。

光波导（optical waveguide）是引导光波在其中传播的介质装置，又称介质光波导。光波导有两大类：一类是集成光波导，包括平面（薄膜）介质光波导和条形介质光波导，它们通常都是光电集成器件（或系统）中的一部分，所以叫做集成光波导；另一类是圆柱形光波导，通常称为光纤。

如图1.1.4所示，（a）、（b）都是圆柱形波导结构，中心（纤芯）为高折射率的圆柱形介质，其周围（包层）为低折射率的圆柱形介质。在圆柱形波导结构中，按照纤芯的折射率分布形状不同，分为阶跃折射率型光纤［图1.1.4（a）］，和渐变折射率型光纤［图1.1.4（b）］。前者纤芯的折射率为常数，而后者纤芯的折射率相对于纤芯的半径（r）呈α次方变化。图1.1.4（c）为用低折射率的平板介质夹着高折射率的平板介质形成的平板波导。图1.1.4（d）是用低折射率的介质包围着高折射率的矩形介质，形成的矩形波导结构。

2）波动理论

（1）波动方程

光是一种高频率的电磁波，光以电磁波的形式传输，电场和磁场结合形成光波。通常以麦克斯韦方程组进行分析。麦克斯韦方程是从基本的实验现象推导而来，包括库仑定律、安培定律和法拉第定律。一般可写成：式中，D为电位移；H为磁场强度；B为磁感应强度；E为电场强度；ρf为自由电荷体密度；J为传导电流。

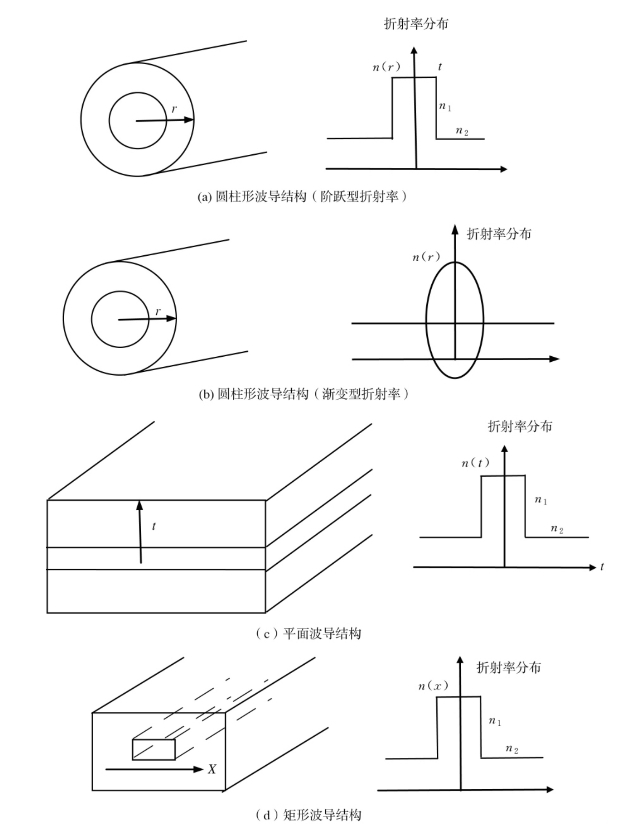
图1.1.4　几种常见波导结构及折射率分布

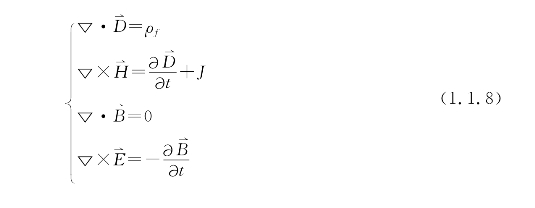
对于介电常数为ε，磁导率为μ的介质，可表示为

在线性、各向同性的电介质中，没有自由电荷和传导电流，麦克斯韦方程组可以简化为：

对于均匀介质来说，由麦克斯韦方程组可以得到：

它们是分析突变（阶跃）光纤的基础。

一般认为，电磁波属于简谐振荡，其波形为正弦或余弦函数。假设认为光纤没有能量损失，那么E的强度沿z方向是均匀分布的，但与z无关，是r，φ的函数Ez（r，φ）（图1.1.5）。假定突变型光纤纤芯半径为a，折射率为n1，包层折射率为n2，并且认为包层无限伸展，并且进一步假定场量随时间t和坐标轴z的变化规律以及方位角的依赖关系为Z（z）T（t）＝ei（ωt－βz＋mφ）。

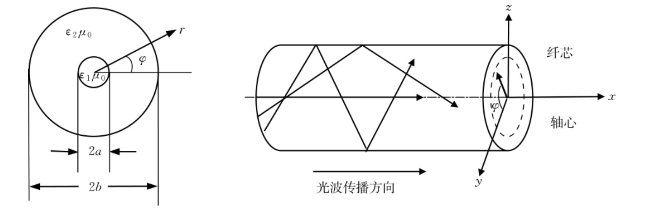
图1.1.5　突变型光纤结构及波导的传播

对圆柱坐标系，据式（1.1.11）和式（1.1.12）的Z向投影，即可得到Ez和Hz所满足的波动方程：

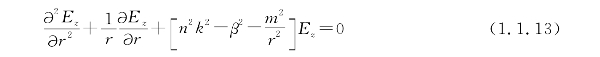
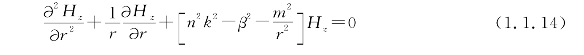
式中，为真空中的介电常数；εr为介质的相对介电系数；n为介质的折射率，k＝2π／λ为真空中的波数，λ为真空中的波长。

假设：

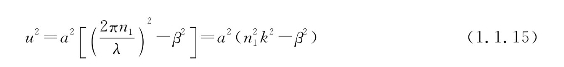
并且

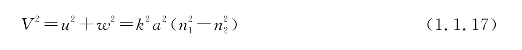
式中，分别为纤芯、包层的折射率；a为纤芯半径；u，w为纤芯、包层的横向传播常数；V为归一化频率。

利用上面假设的参数u，w，式（1.1.13）和式（1.1.14）可改写成式（1.1.18）及式（1.1.19）形式，可以得到贝塞尔方程：

纤芯区

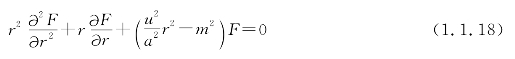
包层区

为简化书写，以上公式中，用F来代替（Ez，Hz）中的任一个，可将Ez和Hz的波动方程合写成一个。

求解方程，需要知道初始条件和边界条件。对于单模光纤来说，边界条件就是纤芯和包层的边界情况，在纤芯和包层交界面上的电场和磁场是连续的。如图1.1.6所示，光纤轴心上（r＝0处）场应为有限，所以在纤芯区选Jm（ur／a）作为式（1.1.18）的解。

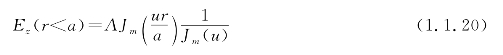
式中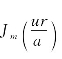，是变数为的m阶贝塞尔函数。

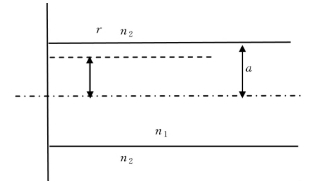
图1.1.6　阶跃光纤结构

当r→∞处的场成为衰减场时，在包层区应选作为式（1.1.19）的解。

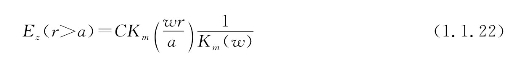
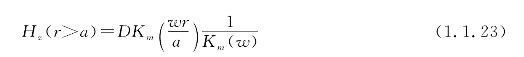
式中，是变数为的l阶对包层区域修正的贝塞尔函数。

以上的A，B，C，D为激励条件所决定的常数。

将麦克斯韦方程组在圆柱坐标系中展开，就可以得到纤芯、包层区的其他场分量的具体表达式。

根据电磁场理论，电磁场的切线分量在纤芯—包层界面处应该连续，即在r＝a处，应有：

自然地，由式（1.1.20）—式（1.1.23）可知，Ez，Hz已自动满足边界条件要求。由Eφ，Hφ应满足的边界条件可以导出突变光纤波动方程的特征方程：

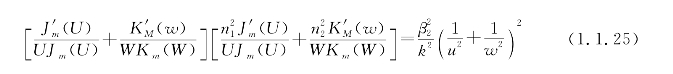
弱波导条件下，波动方程为

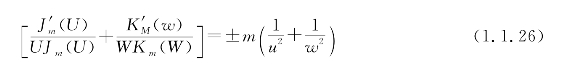
这是一个典型的本征方程，其本征值为β，也就是待求的传播系数，当给定波导的边界条件时，求解波导方程可得本征解和相应的本征值。通常将本征解定义为“模式”，m＝1，2，3，…。如果每一个m代表1个模，光在光纤中传播可以有很多个模。

一个特定模式的传播系数β随归一化频率V的减小而减小，直到达到n2k。对于特定结构参数的光纤，归一化频率随波长增大而减小。当波长增大时，存在的模数减小，直到只有基模存在。远离截止点时，传播系数β及有效折射率可近似为

式中，。

基模（即LP01模或HE11模）的存在不受波长限制，因为其截止频率Vc＝0，对应于无限大的波长。

（2）圆波导的模式

麦克斯韦方程的一个解即对应一个模式，对应着电磁场在光纤中的一种分布形式。按分布形式，模式可以分为以下几种类型：

①横电模（TE）：z方向上的电场分量为0，或电场分量垂直于z，Ez＝0，Hz≠0；

②横磁模（TM）：z方向上的磁场分量为0，或磁场分量垂直于z，Ez≠0，Hz＝0；

③横电磁模（TEM）：z方向上的电场和磁场都为0，Ez＝Hz＝0；

④混合模（HE or EH）：z方向上的电场和磁场都不为0，根据场的纵向分量Ez和Hz的贡献大小，标记为HE（Ez＞Hz）相反EH（Ez＜Hz）。

图1.1.7　对称平板波导中几个低阶传导模的电场分布

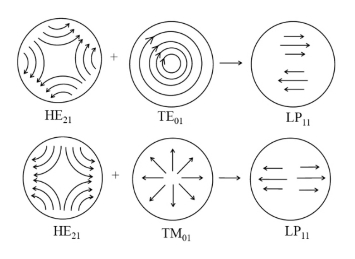
图1.1.8　LP11模的四种可能分布

为了便于理解圆波导中的模式理论，先定性了解图1.1.7所示的平板介质波导中的低阶横电模式的场分布。事实上，平板波导的剖面与沿光纤轴切开得到剖面是相同的。这种波导的芯是由折射率n1的介质平板构成，波导芯被夹在折射率为n2＜n1的两层介质之间，n2是包层介质折射率。

根据场分布曲线可以看出以下几个特点：

①导波模的电场并不完全限制在中心介质波导中，而是部分进入包层，低阶模集中在平板中心附近（亦即光纤芯轴附近），只有少量电场能量进入包层。但对高阶模场，则趋于向波导边缘地带分布，也就是说会有较多的能量进入包层。

②它们的强度在纤芯区域简谐变化，在包层按指数衰减。

③模式的阶数等于波导横向场量零点的个数。光的入射角越小，激发的模式阶数越低。

在弱波导中光纤的HEm＋1，n和EHm－1，n模对都有十分近似的电磁场分布和几乎相等的传播常数，因此，HEm＋1，n和EHm－1，n模是简并模，将这样的简并模称线偏振模，标记为LPmn（Linearly Polarized），它一般是几个真实模的叠加，脚标m，n分别表示该模的电磁场形沿方位角向和沿径向的变化状态的阶数。

对应于每一个LPmn模，一般有四重简并：两种正交的偏振方向和两种可能的方位角分布（即“sin”“cos”两种函数的选择）。图1.1.8给出LP11模分布。

LPmn模与真实模HEm，n和EHm，n（或TM0，m，TE0，m）间的对应关系举例如下：

LP01→HE11；

LP11→TE01，TM01，HE21；

LP21→EH11，HE21；

LP02→HE12；

LP12→TE02，TM02，HE22。

从能量分布看，圆柱空心波导中的低阶模能量集中在波导中心，而模式阶数越高，横截面直径越大，能量分布越分散，图1.1.9为圆柱空心波导能量分布。

图1.1.9　圆柱空心波导能量分布

单模光纤只有最低阶模HE11模式存在，它的光纤横向光斑图类似于图中左上角的“00”截面图。

通过确定的光纤芯包层边界条件和复杂的数学公式计算，可以得到除了支持有限个传导模式外，在光纤波导中还有无限多具有连续谱的辐射模。当传播系数β满足条件n2k＜β＜n1k时（k是传播常数），光纤中存在的是传导模。在β＝n2k时，这个模式将不再能被传导，即被截止。因此，当频率低于截止点，即β＜n2k时，会出现辐射模，辐射模在包层中辐射并将被损耗。辐射模的存在是由于光线进入光纤的入射角度超出最大允许角θc，导致光在光纤芯包界面产生折射的结果。包层辐射模会与导波模分布在包层的能量耦合导致导波模的功率损耗，因此需要抑制。一些高阶模的能量在沿光纤传播过程中连续辐射出纤芯，很快衰减并消失掉，这就是泄漏模。

（3）归一化频率（V）

与截止条件相关的一个重要参数是归一化频率V，定义为：

它是一个无量纲的数，其值决定了光纤可以支持传播多少个模。除了最低阶的LP01模（称为基模）以外，每个模式都有唯一一个可以达到的极限V值（不同的模式有不同的极限V值），使得β＝n2k，从而导致该模式截止。当V≤2.405时，高阶模会被截止，只有LP01模存在，这是单模光纤工作的基本原理。其中，一般把紧邻基模的次高阶模LP11所对应的最大截止波长称为单模截止波长λc，即V＝2.405时所对应的波长。这意味着，当作波长λ＜λc时，多模传播；当工作波长λ＞λc时，实现单模传输。

V是判断单模和多模光纤的标准。从式（1.1.29）可以看出，让V变小的一个途径就是减小光纤半径a的值，所以单模光纤半径比多模光纤小。

根据式（1.1.29），也可以推导出单模光纤的截止波长：

当然，该截止波长只有理论意义，工程中单模光纤的截止波长是由光纤制造厂在拉丝后进行测量。

当V＞2.405时，光纤可以支持多个传输模式，即多模光纤。用M表示多模光纤的模式总数，当M比较大的时候，M与V之间存在近似关系：

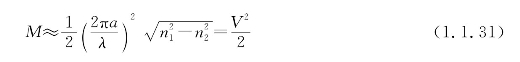
1.1.1.3　光纤中的光线传输

当一束光线从光纤端面进入光纤时，光线有两种可能的运行轨迹：一种是光线始终在直径平面内传播，这种光线成为子午光线，如图1.1.10（a）所示；另一种是光线在传播过程中，其传播时的路径不在同一个平面内，并且不与光纤中心轴相交，这种轨迹的光线称为斜射光线，如图1.1.10（b）所示。

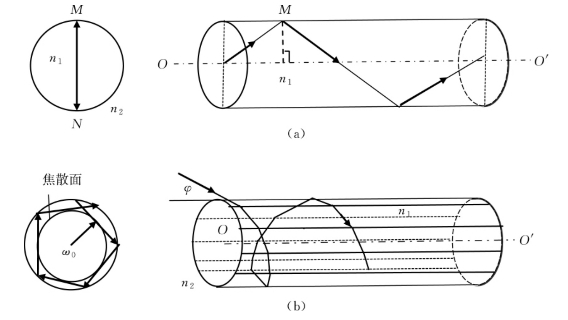
图1.1.10　子午线传播和射线传播

子午光线和斜射光线都服从光线的反射定律，只要是光纤直径均匀，这两种光线都能在光纤内进行若干次的全反射，从光纤的一端传到另一端，但是并非所有从空气中入射到端面的光线都能传播到终点。

通过子午线来分析光在光纤中的传播，如图1.1.11所示

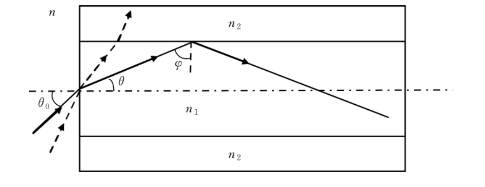
图1.1.11　光线在子午线上的传播

约束光线产生全反射的最小入射角应满足式（1.1.4），即：

从空气中射入的光线，其最小入射角应满足：

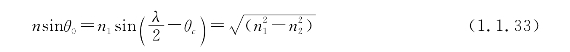
投射到光纤端面的光线中，只有小于最小入射角的光线才能进入纤芯，并在芯包界面上被全反射，继续向前传播。

只有处于光纤端面最大接受角φm的圆锥体内的光线才能在光纤中传输。处于该圆锥体之外的光线，尽管射入了光纤中，但由于不能形成全反射，只能变成折射光线进入包层辐射出去。因此，φm是光纤的一个重要参量。

光线射入光纤，需要通过凸透镜聚光。理想状态，如图1.1.12所示，平行光进入光纤芯层，效率最高。但并不是所有光线都是理想的子午光线，而且射向透镜的也并非平行光，如果光路没有修正，将导致部分信号丢失，如图1.1.13（a）至（d）所示。

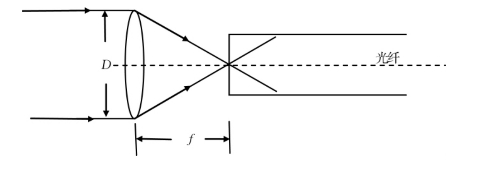
图1.1.12　光线进入光纤中的理想状态

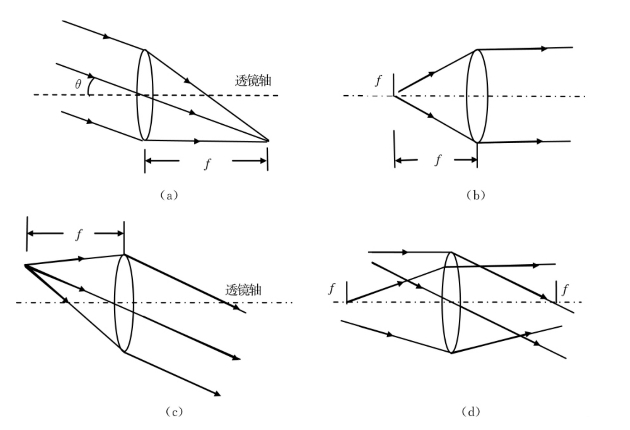
图1.1.13　光线以任意方向进入光纤示意图

1.1.1.4　数值孔径（Numerical Aperture，NA）

光纤端面在允许的最大入射角时射入光线，光纤收集光的能力，可以用数值孔径加以衡量。数值孔径还可以用来计算光源与光纤间的功率耦合效率。

NA是一个小于1的无量纲的数，其值通常在0.14～0.50。NA大，有利于光耦合，但是NA太大的光纤模畸变加大，使得通信带宽较窄。

对阶跃光纤来说，其数值孔径

式中，Δ＝（n2－n1）／n1为芯包相对折射率差。

对梯度光纤来说，其折射率分布

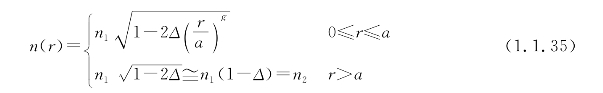
式中，n1为轴心上的折射率，n2为包层折射率。

在离纤芯距离r处的数值孔径为：

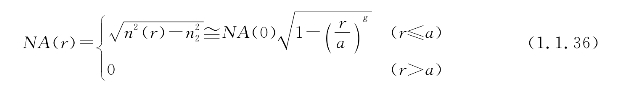
式中，NA（0）为轴心上的数值孔径。

梯度光纤的数值孔径如图1.1.14所示。

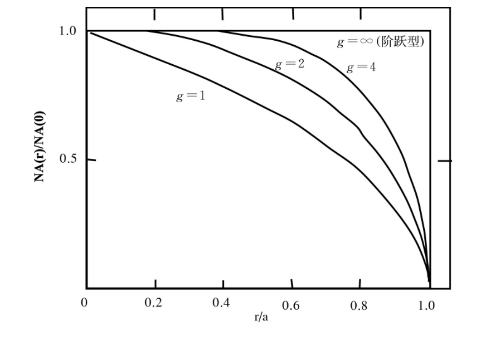
图1.1.14　梯度光纤的数值孔径

1.1.1.5　模场直径（MFD）

模场直径是单模光纤所特有的一个重要参数。它的取值和容差范围与光纤的连接损耗和抗弯特性有着密切的关系。此外，还能由模场直径随波长的变化谱来确定单模光纤的截止波长，并能估算出该光纤的色散系数。因此，在光纤生产、光缆敷设、施工接续和实际使用中，人们非常重视这一参数。(www.xing528.com)

单模光纤中只能传播LP01模（基模）。通俗地说，模场直径就是单模光纤中光斑的大小，模场就是光纤中基模场的电场强度在空间的分布。之所以用模场直径的概念，是因为单模光纤中的场并不是完全集中在纤芯中，而是有相当部分的能量在包层中，所以不宜用纤芯的几何尺寸作为单模光纤的特征参数，而是用模场直径作为描述单模光纤中光能集中的范围。

由于基模场是一个渐变形分布，没有明显的边界（图1.1.15）。所以，对模场直径的定义也比较复杂。对于阶跃型光纤，基模场是零阶贝塞尔函数，近似高斯函数，取场强分布最大值的1／e，也即光强分布最大值的1／e2来定义基模光斑的大小。高斯分布只适用于理想阶跃单模光纤，而实际中的光纤模场分布并非都是高斯分布，因此随后又有用高斯拟合和大注入效率法进行定义。

高斯分布的电场为

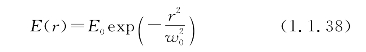
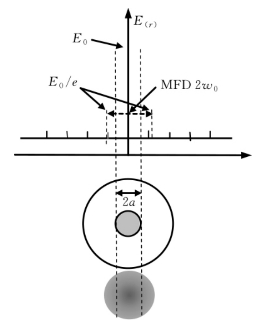
图1.1.15　基模近场功率分布

因此，定义光功率为e－2E0时的光场半径宽度（E0为轴心的光功率）为模场直径（MFD），即光纤截面的光斑尺寸：

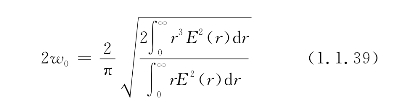
MFD定义的方法很多，式（1.1.39）只是采用远场强度分布的定义式。具体的定义和测量方法在本书第9章光纤测量章节予以介绍。

通常单模光纤模场直径比纤芯直径大10%～15%，模场直径可估算连续损耗、弯曲损耗和微弯损耗等。

1.1.1.6　光纤的折射率分布

光纤的折射率分布决定了光纤的性能。因此，必须根据光纤的类型进行合理的折射率分布设计，折射率的分布设计应符合：衰减系数尽可能小，合理的色散特性，更宽的工作波长，剖面结构重复性好，便于生产等。

1）多模光纤

（1）阶跃型多模光纤

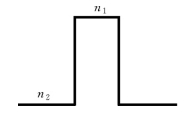
图1.1.16　阶跃型折射率分布

光线在光纤中能够传播的前提条件是实现全反射。光纤芯的折射率n1会稍大于包层折射率n2，而对于阶跃型折射率光纤，在芯层和包层之间的界面上，折射率突增，呈台阶状。

图1.1.16为阶跃型多模光纤折射率结构。

该剖面折射率结构光纤，结构简单，制作容易，具有较大的芯径和大的数值孔径，容易与光源耦合，但是由于存在较大的模间色散，带宽比较小，传输容量有限，无法适应长距离通信要求，所以现在使用不多。

（2）梯度型多模光纤

人们为了减小阶跃型多模光纤的模间色散，设计了一种抛物线形状的折射率光纤，如图1.1.17（a）所示。光纤芯轴折射率最大，这种光纤具有很小的模间色散和很高的带宽。新一代梯度型折射率分布的多模光纤采用内包层折射率下陷型设计，如图1.1.17（b）所示，除具有良好的抗弯曲性能外，还提高了光纤的数值孔径，有效降低了多模光纤的衰减。

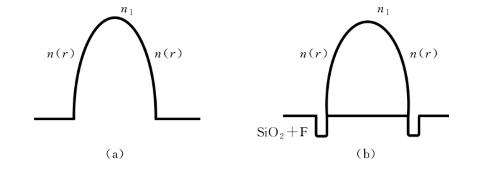
图1.1.17　梯度型多模光纤折射率分布

2）单模光纤

（1）非色散位移单模光纤（G.652光纤）

G.652光纤最佳工作波长在1310nm附近，零色散波长也在1310nm。最常见的两种折射率分布剖面结构为：简单阶跃匹配包层和下陷包层。

阶跃匹配包层采用GeO2来提高纤芯折射率，光纤的抗弯性能稍差。下陷包层是在内包层掺杂氟来产生下陷的折射率，这样在纤芯中掺杂少量的Ge就获得了较大的总相对折射率。这种光纤结构大大改善了光纤的抗弯性，减小了衰减。折射率分布剖面结构如图1.1.18所示。

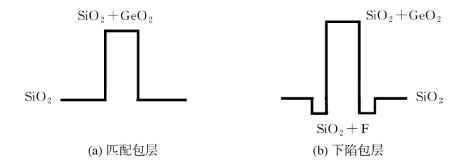
图1.1.18　G.652光纤折射率分布

（2）色散位移单模光纤（G.653光纤）

G.653光纤在1550nm波长处实现最小的衰减系数和零色散，而且具有抗弯性能好，接续损耗低等特点。它的折射率分布结构有三角芯、分段芯、下陷包层三角芯和双台阶芯等结构，折射率分布剖面结构如图1.1.19所示。通过调整各部分折射率差和几何尺寸，较容易控制波导色散，以实现零色散波长的移动。G.653光纤目前已经被G.655光纤替代。

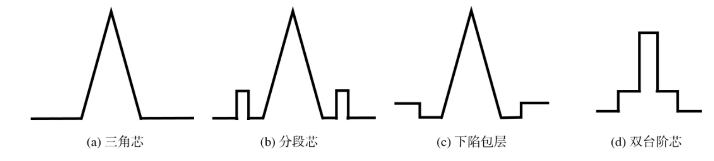
图1.1.19　G.653光纤折射率分布

（3）截止波长位移光纤（G.654光纤）

截止波长位移光纤为1550nm波长，又称为最低衰减光纤。因G.654光纤1550nm波长的最低衰减为0.15dB／km，所以最早主要用于线路距离长、承载信息量要求大的海底光缆。与G.652光纤一样，G.654仍然采用简单阶跃匹配包层和下陷包层等结构。G.652光纤纤芯掺锗，而G.654光纤则是纯SiO2纤芯，以降低光纤衰减，下陷包层是通过石英材料中掺氟材料，用于防止由于光纤模场直径（MFD）增大带来的弯曲性能恶化。下陷包层的掺杂浓度和宽度对弯曲性能的改进有明显的效果，一般来说，在光纤的折射率剖面上，下陷包层的面积越大，光纤的抗弯曲性能越好。随着系统不断升级，G.654光纤大有效面积成为重点研究方向。在新型大有效面积G.654光纤研究过程中，各厂家推出了如图1.1.20所示的多种折射率分布曲线的大有效面积光纤剖面结构设计。图1.1.20（a）、（b）为常规掺氟纯硅芯的大有效面积光纤；图1.1.20（c）为常规掺锗大有效面积光纤；图1.1.20（d）为常规掺锗光纤，并在芯层部分采用环形芯方式的剖面结构设计。

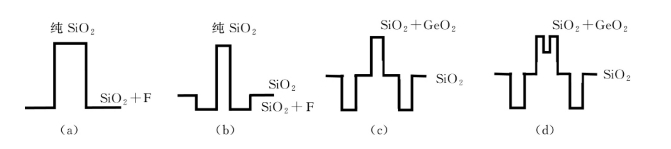
图1.1.20　典型G.654光纤折射率分布

G.654光纤的典型有效面积值为110μm2，130μm2，150μm2，比传统G.652光纤典型值80μm2分别增加了37.5%，62.5%，87.5%，大大提高了进入光纤的光功率，降低了非线性效应。G.654光纤可以分为低损耗大有效面积光纤和超低损耗大有效面积光纤。

（4）非零色散位移单模光纤（G.655光纤）

G655光纤的设计目的是为高速率、大容量和远距离的密集波分复用（DWDM）传输系统提供一种合适的光纤。G.655光纤特性：在1550nm工作窗口的色散系数不为零，损耗最小，以抑制DWDM引起的非线性效应及四波混频（FWM）。

非零色散位移光纤的设计通常从两方面着手：一是选用各种函数形式的梯度型折射率分布的纤芯来调节其色散特性；二是采取多包层的折射率分布。多包层剖面对单模光纤的波导色散和截止波长有明显的调节作用。二者的综合可在广阔的范围内得到所需的色散特性。

各个光纤制造厂的G.655光纤的折射率剖面都不同。但设计的太过复杂，不仅性能稳定性受影响，而且传输特性也会发生变化。

图1.1.21列出几个典型的G.655光纤的折射率分布剖面结构图。

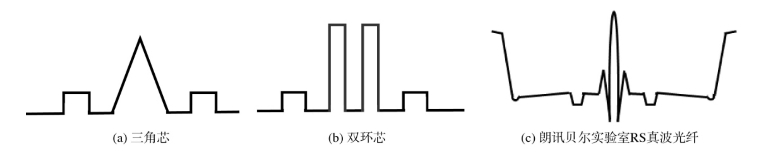
图1.1.21　典型G.655光纤折射率分布

图1.1.21（a）的三角芯（小有效面积G.655光纤）和图1.1.21（b）的双环芯（大有效面积G.655光纤）中的第一个环具有可移动零色散波长的作用。这两种剖面结构的外环对实现大有效面积和微弯曲损耗都起着关键作用，其可将光从中心尖峰处吸收出来，以达到较大的场分布。因此，可通过降低尖峰功率来增加有效面积，并且通过防止光泄漏到包层而改善微弯性能。两种结构的区别在于，三角芯具有略低的衰减，双环芯则具有稍大的有效面积。图1.1.21（c）为朗讯贝尔实验室最早研究的一款折射率分布非常复杂的真波光纤。

（5）宽带光传输用非零色散位移单模光纤（G.656光纤）

人们为了能够在较宽的波段内得到平坦的小色散特性，通过调整纤芯与内包层折射率环之间的下凹环的宽度与深度，以达到满足色散平坦的新要求，从而研制出G.656光纤。

最初色散平坦光纤折射率剖面结构为双包层型。该结构能使光纤两个零色散点分别在1210nm和1550nm，且光纤在1210～1550nm波长范围内色散呈平坦分布，数值较小。双包层型光纤有内外两个包层，内包层比外包层折射率要小，从而形成了一个折射率下凹的深沟限制色散的扩展，但缺点是弯曲损耗大。

三包层和四包层型是在双包层型基础上发展起来的，它的结构特点是在双包层型的内外包层加入一凸起的折射率环，其色散特性和抗弯能力优于双包层型。但是它们结构复杂，制造困难。这些单模光纤的纤芯折射率分布结构可以是梯形、三角形、矩形、高斯型等。

图1.1.22所示为两种G.656光纤的折射率结构分布，从外形看，二者是比较接近的。这里的G.656光纤各部分全部采用阶跃型折射率分布设计。

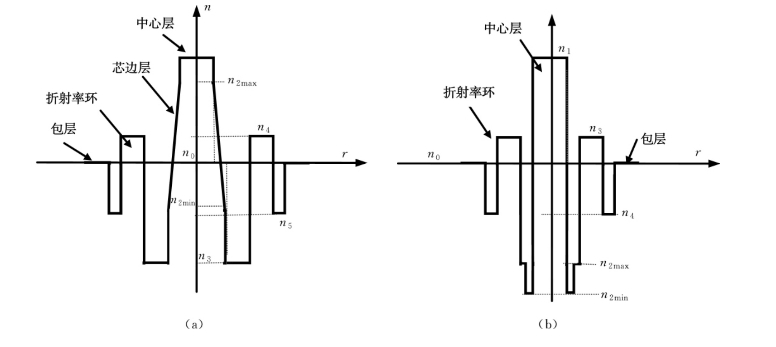
图1.1.22　G.656光纤折射率分布

（6）弯曲损耗不敏感光纤（G.657）

为提高G.652光纤的弯曲性能，通过降低MAC（MFD／λc）或改变芯包折射率差（Δ）有一定难度，MFD和截止波长λc的改变受到光纤综合性能下降的制约，MFD减小增加了光纤接续的难度。日本藤仓公司通过在包层中引入沿光纤长度方向的气孔以减小包层有效折射率制作孔助弯曲不敏感光纤（图1.1.23），住友电工于2001年宣布HALF（Hole Assisted Light guide Fiber）光纤，也是一种空心光纤（图1.1.24）。这类空心光纤与光子晶体光纤一样，熔接过程中可能会引起气孔的闭合和塌缩，增大了熔接损耗，大规模的批量生产也很困难。2004年，藤仓公司报道开发了沟助G.657光纤，其折射率分布剖面如图1.1.25所示。2006年，荷兰德拉克推出BendBrightXS光纤，它在包层中增加了一个下陷沟槽，而且沟槽的深度（Δ3）与纤芯折射率高度（Δ1）接近。美国康宁（Corning）公司在2007年推出nanoSructuresTM技术的新型弯曲损耗不敏感光纤——ClearCurveTM，其与沟助光纤相似，只是在包层中用纳米结构来代替下陷层化学剂掺杂，Corning公司G.657光纤截面如图1.1.26所示。

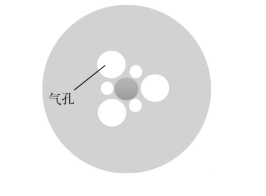
图1.1.23　藤仓孔助光纤截面示意

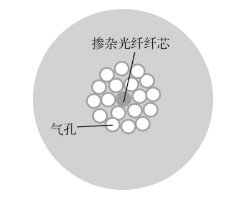
图1.1.24　住友电工HALF孔助光纤截面示意

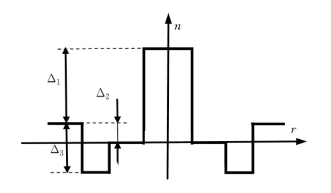
图1.1.25　藤仓沟助G.657光纤折射率分布

图1.1.26　康宁ClearCurveTM光纤截面示意

（7）少模光纤

少模光纤（Few－Mode Fiber，FMF）是一种新型的光纤，利用空分复用技术，在同一根光纤中实现多信道传输。少模光纤纤芯面积足够大，是一种足以利用几个独立的空间模式传输并行数据流的光纤。与单模光纤和多模光纤不同的是，单模光纤只传输LP01模或HE11模，多模光纤则传输无穷多个模。少模光纤经过设计，一般传输2～10个模。目前少模光纤主要是多芯结构或多空包层结构，或经过对纤芯折射率分布进行设计优化模式耦合。

少模多芯光纤中每个纤芯折射率分布可以相同，也可以不同，有阶跃型、渐变型及多包层型等。图1.1.27为几种常见的少模光纤折射率分布类型。

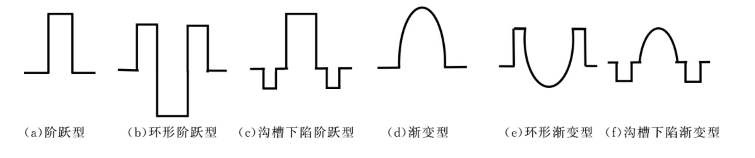
图1.1.27　少模光纤纤芯折射率分布类型

1.1.1.7　光纤传输特性

1）衰减（Attenuation）

衰减是光纤传输最基本，也是最重要的传输参数，有时又被称为损耗。在光纤还没有被用于通信时，1966年英籍华裔科学家高锟（C.K.Kao）博士和霍克姆（Hockham）就预言，利用玻璃可以制成衰减为20dB／km的通信光导纤维（光纤），而当时世界上最优良的光学玻璃衰减达1000dB／km。1970年，美国康宁（Corning）公司制作成世界第一根光纤，从此世界进入了光纤通信的时代。

衰减表明光纤对光能的传输损失，也就是光经过光纤的传输，其光功率减少的量。它影响着光纤传输距离，也是对光纤质量的评判基础。光在光纤中传输时，平均光功率沿光纤长度是按照指数规律减少。即：

式中：P（0）——注入光纤中测试起点的光功率；

P（l）——光传输到距离l处的测试终点的光功率；

α——衰减系数。

（1）衰减系数

由于衰减跟长度密切相关，为评价光纤传输性能的优劣，一般用衰减系数表示。

衰减系数α的定义：单位长度l光纤上的光功率损耗。l为传过光纤截面点A到点B的长度，PA，PB为A点和B点的光功率。计算公式为

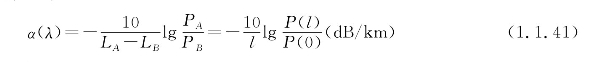
式中，α（λ）为波长在λ处的衰减系数，与光纤长度无关。P（l），P（0）为测试点终点和起点之间的光功率。

衰减系数是一个平均概念的量。光纤材料的均匀度差，将增大光纤损耗的不均匀性。衰减测量的方法有多种，一般有截断法、插入法和后向散射法（OTDR）。目前用得最多的就是后向散射法。

（b）衰减系数谱

衰减系数谱有时也简称为衰减谱。对SiO2光纤来说，在不同的波长下有相应的衰减系数。把各个波长测量所得的衰减系数相连，即可得到图1.1.28所示的光纤衰减系数谱。形成光纤衰减的原因有多种，一般为光纤的材料和结构，还有光纤制造工艺等。

（3）衰减产生的原因

光纤中的光衰减（损耗）包括光纤材料本身的固有损耗、光纤的弯曲损耗、接续损耗和光纤制造缺陷等。

光纤的固有损耗是光纤材料对光波的散射、吸收所产生的损耗，主要因素有：①散射损耗；②在红外、紫外区玻璃的固有吸收；③杂质（OH－离子和过渡金属离子）吸收；④光纤结构不完善所产生的辐射和散射。

散射损耗是光能以散射的形式辐射出光纤外而造成的。光纤中产生的散射损耗主要有：瑞利散射、米氏散射、受激布里渊散射、受激拉曼散射、附加结构缺陷和弯曲散射、泄漏。

光纤材料中比光波长小得多的粒子引起的散射称为瑞利散射。与光波同样大小的粒子引起的散射称为米氏散射。

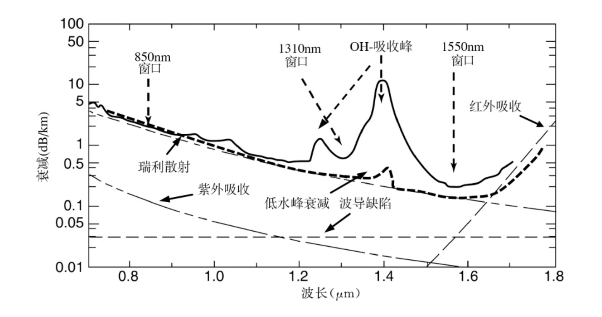
图1.1.28　光纤衰减谱

引起光纤损耗的散射主要是瑞利散射，它是纤芯折射率的微小变化所产生的散射现象，其损耗与短波长的四次方（λ4）成反比。在光纤制棒及拉丝过程中，由于热量的不均匀分布，导致微观物质成型过程中的密度不均匀，进而使折射率产生波动，这种不均匀性在光纤拉丝冷却后被固定了下来。一般地，玻璃转变温度高、组成复杂的具有瑞利散射损耗大的趋势。受激布里渊散射和受激拉曼散射，则存在于光能密度超过某一高值，光与媒介相互作用产生的，如非线性散射。

杂质吸收光能导致损耗，如OH－离子在2.8μm波长有吸收峰，二、三次谐波的吸收分别发生在1.4μm，0.94μm。但是，随着制造技术的进步，OH－离子的吸收在减少。在可见光到近红外光（1.6μm）范围内，除瑞利散射以外的各种因素几乎完全被消除。

光纤结构的缺陷必然会引起光散射。现在随着光纤制造技术的日益完善，对由于结构缺陷而引起的损耗几乎可以不考虑了。

弯曲损耗分两种：宏弯损耗和微弯损耗。所谓微弯曲是指光纤受到不均匀应力的作用，光纤轴产生的微小不规则弯曲。其结果就是传导模变换成辐射模而导致光能的损失。

减小微弯曲损耗的方法有多种，例如：在光纤玻璃包层外通过二次固化，且内层采用比外层模量小一些的树脂，相当于在光纤中间设置了一个缓冲层；光缆采用松套充油膏的结构等避免光纤直接受到侧压力影响等。光纤成缆后，光缆设计不合理，受温度、侧压力、拉力等影响，光纤同样会存在微弯损耗。

宏弯损耗是光纤弯曲时，光波从直线部分进入弯曲部分，传导模转变为辐射模而产生损耗。在光纤成缆、运输、施工以及敷设等环节，都可能会因光缆弯曲半径过小而导致光纤损耗的增大。在成缆工艺中，光纤余长是一个非常重要的参数。

宏弯损耗和微弯损耗不是孤立的存在，在某些情况下，如光缆曲率半径过小，光缆余长过大或过小等，都可能存在两种形式的弯曲损耗。

2）色散（Chromatic Dispersion）

所谓色散，本来是指折射率等物理常数随频率（波长）而变化的现象。在物理光学中，色散是表示由于某种物理原因使具有不同波长的光在介质中发生的分散。在纤维光学中，色散主要是光脉冲经过光纤传输后在输出端发生能量分散，导致传输信号畸变。在数字通信系统中，由于信号的各频率成分或各模式成分的传输速度不同，在光纤中传输一段距离后，将互相散开，脉冲展宽。严重时，前后脉冲将互相重叠，形成码间干扰，增加误码率，影响了光纤带宽，限制了光纤的传输容量。

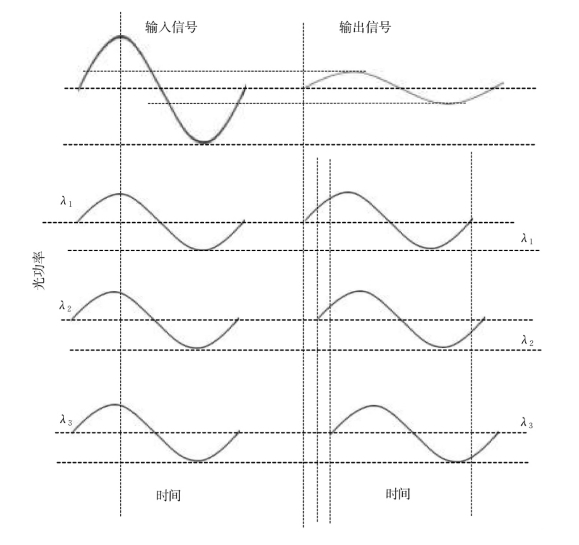
如图1.1.29所示，光脉冲通过色散材料传输后，不同波长的脉冲波λ1，λ2，λ3以不同的速度到达终点，信号叠加后产生脉冲的展宽，信号的失真。图1.1.30表示色散引起脉冲信号展宽后，振幅的减小。

图1.1.29　不同波长的光脉冲以不同的速度到达终点

多模光纤的色散主要包括：模间色散、材料色散、波导色散等。其中模间色散占主要成分，它最终限制了多模光纤的带宽。单模光纤是传输一个模的光波导，没有模间色散，因而带宽很高。色散也是单模光纤的重要参数之一。研究光纤的色散特性，对合理地设计剖面结构，改善光纤的传输特性是极为重要的。单模光纤的色散主要包括材料色散、波导色散和折射率剖面色散：

（1）材料色散。由于纤芯、包层材料的折射率是光频（波长）的函数，不同的频率传输速度不同，对于谱宽较宽的信号，经过传输后产生脉冲展宽的现象。

（2）波导色散。由于某一模的传播常数β是光频（波长）的函数，不同频率下，对于同一模式，它的传播常数随之变化而产生的群速之差使脉冲展宽的现象。

（3）折射率剖面色散。由于纤芯、包层相对折射率差Δ是波长的函数而引起的脉冲展宽现象。一般说来，纤芯、包层材料折射率随波长变化的比率近似相同，Δ近似不变，这项的贡献很小，可以被忽略。

对单模光纤来说，波导色散一般为负值，材料色散为正值，日常所说光纤色散一般指波导色散和材料色散的总和，如图1.1.31所示。

?

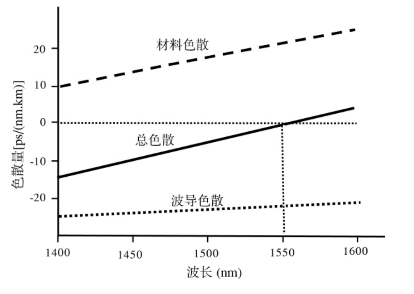
图1.1.31　单模光纤色散组成

严格说来，偏振模散也属模间色散，但其数值比较小，只是当速率为10Gb／s以上，其对系统才会有较大影响。下一节将专门对偏振模散进行分析和说明。

描述光纤色散程度常用时延差τ来表示。即在光纤中，不同速度的信号传过同样的距离所需的时长不同，出现时延。时延差越大，色散就越严重。光纤的色散特性用传输常数β对光频的泰勒展开来描述，即：

式中，ω0为中心频率，展开系数为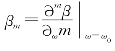。前两个系数具有特定的含义，即

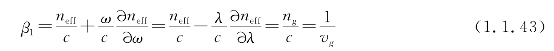
上式表明群速度vg是波长的函数，称为群速度色散，群速度色散导致脉冲传播的延迟和展宽。通常用色散系数D来描述单位长度和单位线宽的群时延，单位为ps／（nm.km）。

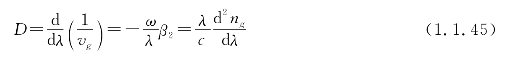
式中，ng为群折射率。

常规G.652单模光纤最小色散位于1300nm波段，而最低损耗位于1550nm波段，该处色散系数为－17ps／（nm·km）。

而时延差τ为：

τ还可以表示成β对波长的一阶导数形式：

3）偏振模散（Polarization Mode Dispersion，PMD）

偏振是与光的振动方向有关的光性能。光纤中存在两个相互独立且偏振面相互正交的简并模，由于光纤结构的不完整，使得两个相互简并的模式在光纤中以不同的相速度传播，光纤对它们具有不同的有效折射率，即双折射效应。并且，两个简并模在传播时会产生相位差。

由于光纤并非理想的圆对称，因此会产生偏振模散。光作为电磁波，在光纤中沿轴向（z向）传输过程中，同时分解成y两个方向的振动。光的传输速度与折射率成反比，折射率越高，传输速度越小。由于光纤纤芯折射率的变化，在x，y两个方向振动的波传输到终点时，将产生时间差，如图1.1.32所示。图（a）x和y轴折射率相等，光速度一致，图（b）x轴光线的速度比y慢，达到终点将会形成时间差，如图1.1.33所示，光经过双折射后导致脉冲时延。

每个轴上传播的光波代表一个偏振“模”，两个偏振模到达的时间差称为偏振模散PMD，实际上PMD是光脉冲群时延的平均值。PMD的度量单位为皮秒（ps），1ps＝10－12s，PMD与光纤长度的平方根以及偏振模系数成正比。一般用偏振模散系数（PMDcoeff）来表示光纤的PMD特性。PMDcoeff的单位表示为ps／km2。

造成单模光纤中PMD的内在原因是纤芯的椭圆度和残余内应力，它们改变了光纤折射率分布，形成双折射，从而引起相互垂直的本征偏振以不同的速度传输，进而造成脉冲展宽，形成群时延；外因则是成缆和敷设时的各种作用力，即压力、弯曲、扭转及光缆连接等都会引起PMD。

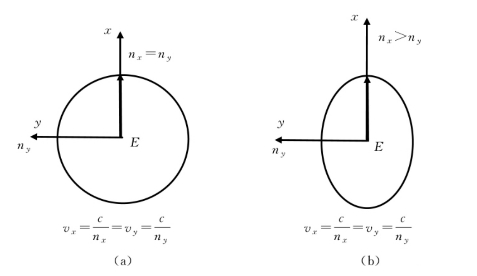
图1.1.32　不同的折射率，光线传输的速度不一致

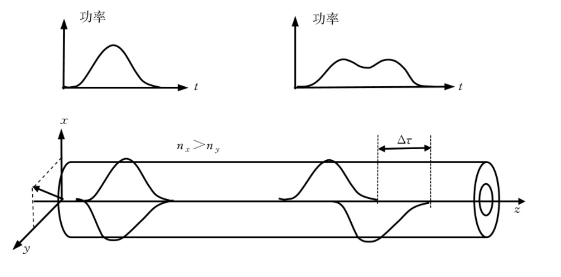
图1.1.33　光经过双折射后导致的脉冲时延（图片来源：康宁公司PMD介绍）

在2.5Gbit／s系统中，PMD影响并不大，但当系统超过10Gbit／s时，PMD造成的影响就越来越大。日常常用光缆链路PMDQ来表示光纤PMD性能。

4）光纤非线性效应

在大容量、高速度的密集波分复用光纤通信系统中，由于光纤传输的工作波长多、功率大，光信号在光纤中会产生各种非线性效应。通常，将不同的非线性现象自身出现的光功率的大小称为“阈值”。如果不对这些非线性效应加以适当抑制，它们将会严重影响系统的性能和限制再生中继距离。

光纤的非线性可分为两类：受激散射和折射率扰动。

对单信道系统，非线性效应主要是自相位调制（SPM）和受激布里渊散射（SBS）；多信道系统，则来源于交叉相位调制（CPM）、受激布里渊散射（SBS）和四波混频（FWM）。

（1）受激散射

光信号与光纤中的声波或系统振动作用会产生非线性受激散射。这种相互作用使光散射或将光移至长波长。目前知道的受激散射有两种：受激布里渊散射和受激拉曼散射。

①受激布里渊散射：受激布里渊散射（SBS）是由于光纤中的光信号和声波之间的相互作用所引起的非线性现象。在已知的光纤非线性效应中，SBS的阈值最小，其大小取决于光源的谱线宽和光纤的特性。典型的SBS阈值只有几毫瓦，且与信道数无关，所以SBS是第一个非线性效应，但是它也是一个最容易消除的非线性效应。因为SBS阈值随光源谱线宽的宽度而增大，所以一个增大SBS阈值的简单和实用的方法是用窄、低频正弦信号来调制激光器光源。

②受激拉曼散射：受激拉曼散射（SRS）是光信号与石英玻璃光纤中的分子振动的相互作用而引起的非线性现象。SRS阈值与光纤特性传输的信道数、信道间隔、每个信道的平均光功率和系统的中继距离等有关。对单信道系统而言，SRS阈值约为几瓦，其值远远大于受激布里渊散射（SBS）的阈值。SRS散射光是以前后两个方向传播的，可采用光隔离器来消除后向传输的光功率。

（2）折射率扰动

石英玻璃光纤的折射率在低光功率的作用下是保持恒定的，但是使用掺铒光纤放大器过程中，其高的光功率（光强度）会引起光纤折射率的变化，从而导致光纤非线性效应。折射率变化的关系式如下：

式中：n0——线性折射率；

n2——非线性折射率系数；

P——输入功率；

Aeff——光纤的有效面积。

从式（1.1.48）可以看出，在非线性阈值功率一定的情况下，增大有效面积，允许的最大光纤输入功率就越大。或者说，如果想减小非线性效应的影响，增大光纤有效面积是一个好的办法。但是，追求大的有效面积存在很多制约因素：

①增大有效面积的手段主要是折射率剖面分布的设计，在实现较大的有效面积同时还需考虑光纤的其他参数，包括色散、截止波长，而过于复杂的折射率剖面分布设计，更是增加了制造难度和成本。

②在一定的折射率剖面分布条件下，色散斜率往往与有效面积成正比。为了保证较低的色散斜率，不得不舍弃更大的有效面积。

③光纤的有效面积越大，在泵浦光功率一定的条件下，拉曼增益降低。

所以光纤的有效面积也必须适中，既要能够使光纤具有一定的抑制非线性效应的能力，又要兼顾拉曼放大效率和色散斜率。

折射率扰动引起的非线性效应主要有三种：自相位调制、交叉相位调制和四波混频。

自相位调制。自相位调制（Self Phase Modulation，SPM）是一个脉冲对自身相位的作用而引起的。一次脉冲的边表示一个变时光强，该光强产生一个变时折射率。改变的折射率调制传输波长的相位，进而展宽了传输的光脉冲的光谱。严重的话，在密集波分复用（DWDM）系统中光谱展宽会重叠进入邻近的信道，从而严重影响系统性能。实践中，选用低色散或零色散的光纤消除或减小SPM对系统性能的影响。

交叉相位调制。交叉相位调制（Cross Phase Modulation，CPM）是一个脉冲对其他信道脉冲相位的作用，其产生方式与自相位调制（SPM）相同。CPM与SPM所不同的是：SPM发生在单信道和多信道系统中，而CPM则仅出现在多信道系统中。不同波长的脉冲之间互相作用，会造成光谱的展宽。

在脉冲之间相互作用所产生传输性能下降中，波长色散起着双重作用：一方面色散降低以不同群速度传输的脉冲之间相互作用，另一方面，波长色散暂时扩宽宽谱功率。因此，CMP的作用是复杂的。采用非零色散位移的手段能有效限制CMP。

四波混频。四波混频（Four Wave Mixing，FWM）是指由三个波长的光波混合后产生的新光波，即某一波长的入射光强度改变了光纤的折射率，从而在不同频率处发生相位调制（失调），产生新的波长。

新频率的简化形成可以用式（1.1.49）表示：

式中，i，j，k角标指的是现有的三个EM波的频率，三个波调制后形成了一个新的波，频率为ωijk。

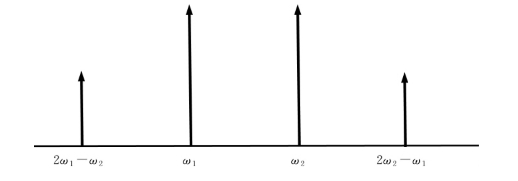
图1.1.34　两个频率波的混合产生两个新的频率

图1.1.34以简单示例表示两个频率ω1，ω2的波混合后，产生的新频率（2ω1－ω2）和（2ω2－ω1）。同样的，三个同传波按式（1.1.50）计算将出现九个新的频率（波长），这些频率的波长与原来的波一起传输，自然消耗了光信号强度。

假设N为现有频率数，新增的频率数：

四波混频（FWM）与信道间隔关系密切，增大信道间隔，可减弱FWM的影响。其对波分复用系统的影响：一是将波长的部分能量转换为无用的新生波长，从而损耗光信号的功率；二是新生波长可能与某信号波长相同或重叠，造成干扰。

由于FWM要求波长匹配，而在光纤的零色散波长附近材料色散对相位失配的影响很小，故FWM最严重。增大光纤的色散有利于克服FWM。此外，还可以通过调整光纤的色散沿长度的变化来破坏波长匹配，抑制FWM。

光纤的非线性效应对光通信系统的传输速率、距离和带宽等带来很多不利的影响。特别是随着DWDM复用波长数量越来越多，注入光纤的光功率越来越大，光纤中光强度越来越高，其非线性效应将越来越严重。新的光纤品种不断推出，实际上很大一部分因素也就是为了消除非线性现象对传输容量的影响，综合考虑光纤的色散和合理分布。

但是，非线性效应也不是一无是处。例如，人们利用受激拉曼散射（SRS）效应制作拉曼放大器以实现对信号光的放大，并广泛应用于40Gbit／s以及C，L，S的全波段DWDM系统。

1.1.1.8　光纤的机械性能

光纤在实际使用过程中，必须具有足够的抗拉强度和抗弯曲强度，以便成缆各工序和敷设过程中光纤不至断裂；在恶劣环境条件下也不应因疲劳而破坏，以保证光纤性能的长期可靠。

从光纤制作到光缆的使用、维护各个环节，对光纤的机械强度特性要求都不同。例如，从拉丝、着色、二次被覆或并带等工序一直到工程敷设都要求具有一定的抗张力以及抗弯曲能力，而敷设后的维护阶段，在各种环境条件下应不容易产生静态疲劳和动态疲劳破坏。

光纤在拉丝过程中，玻璃表面分子的张力作用会产生微裂纹，如果没有树脂涂覆保护，玻璃脆性和抗弯曲性能差的特点将非常明显。而经过树脂涂覆的光纤，将得到380kg／mm2以上的抗拉强度，这个值接近于强度极高的钢琴线（200kg／mm2）的两倍。

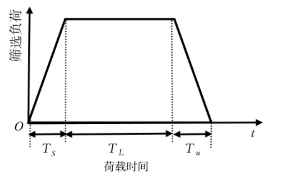
图1.1.35　光纤张力筛选过程中的负荷曲线

注：TS表示筛选开始施加张力（时间从0到正常筛选张力）；TL表示正常筛选张力；TU表示张力开始卸载（时间从正常力值水平到力值为0）。

为了保证光纤具备最基本的强度要求，在光纤制造过程中需进行张力筛选，以便将已经产生较大微裂纹或有其他缺陷的产品暴露而剔除。根据经验，国际电信联盟（ITU－T）标准规定通信光纤不管是多模还是单模，应该受到不小于100kpsi或0.69GPa的筛选应力，按125μm直径计算光纤的筛选张力，最大筛选张力约为8.3N。图1.1.35为光纤张力筛选过程中的负荷曲线。

光纤筛选时间T＝TS＋TL＋TU，一般为1s。

针对一些特殊张力的要求，提高光纤筛选张力或延长光纤筛选受力时间，都是可行的。但光纤筛选不是力值越大或时间越长就越好，也不是筛选次数越多越好，每一次对光纤进行筛选，实际对光纤就是一种伤害，扩大了原有的隐蔽的微裂纹，实际将会逐步降低光纤的机械性能。

由于光纤受环境温度、湿度以及紫外线等影响，特别是光纤在存储期间保护不良，光纤涂层材料性能会下降，最终体现在光纤强度的下降。