YB43020B模拟示波器的性能参数和使用方法解析

【例题11.1】试求如图11.1所示悬臂梁的应变能，梁的抗弯刚度为EI，并求自由端的挠度。

【解】（1）梁弯矩方程为（坐标原点位于自由端，图中未画出）：

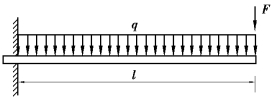
图11.1　例题11.1图

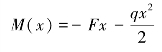
（2）梁应变能计算。

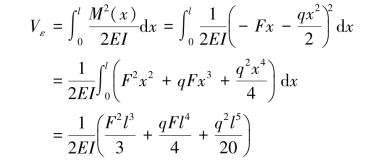
（3）由卡氏定理，自由端挠度为：

【例题11.2】如图11.2（a）所示，轴线为四分之一圆的平面曲杆，A端固定，自由端B受竖直向下的集中力F作用，EI为常数。求B点的竖直和水平位移。

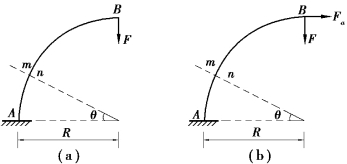
图11.2　例题11.2图

【解】要注意曲杆的内力不仅有剪力和弯矩，还存在轴力，但由于其压缩应变能和剪切应变能远小于弯曲应变能，故忽略剪力和轴力对变形产生的影响。

（1）计算B点的竖直位移。分析图11.2（a）中m—m截面的弯矩为

求偏导数

(www.xing528.com)

代入卡氏定理公式，有

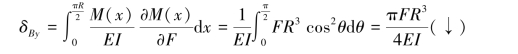
（2）计算B点的水平位移。在B截面施加一虚拟水平力Fa，同理计算得到

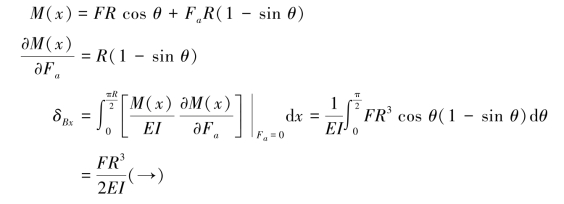
上述结果均为正，表示位移与相应力方向一致。

【例题11.3】计算如图11.3（a）所示桁架各杆的内力。设各杆材料相同，横截面面积相等。

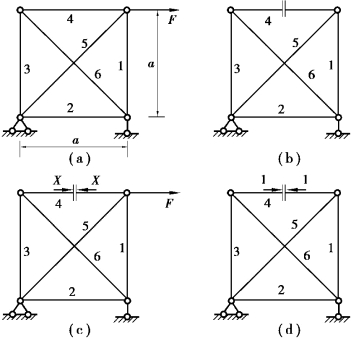
图11.3　例题11.3图

【分析】本题中的支座反力可由平衡条件分析求出，但桁架内部有1个多余约束，所以内力是超静定的。与建立超静定梁的基本静定系类似，去掉某一个多余约束后的静定结构就是基本静定系，例如本题中切开4杆[图11.3（b）]。考虑到桁架中杆件均为二力杆，切开4杆后，代之以多余约束力X，连同结构上原有荷载，就得到了原结构的相当系统，如图11.3（c）所示。比较相当系统和原结构，切口两侧截面的相对线位移应该等于零，也就是相当系统的变形协调条件为：δ4=0。

【解】通过莫尔定理来求解相当系统中切口两侧截面的相对线位移。首先求出相当系统中各杆的轴力FNi，将结果列入表11.1。

表11.1　计算结果表

为求切口两侧截面的相对线位移，在基本静定系的切口两侧截面施加一对方向相反的单位力，如图11.3（d）所示，求出各杆轴力。

根据莫尔定理公式可求出δ4，再代入前面的变形协调条件，有

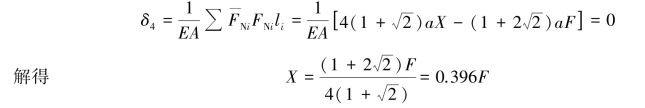
求出X后，代入相当系统中各杆轴力FNi的表达式，就得到了原结构受荷载作用下的各杆实际轴力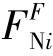，将结果列于表11.1的最后一列。也可以通过卡氏定理求解此题中相当系统切口两侧截面的相对线位移，请读者自行考虑。