如何计算梁AB的工作安全因数？

【习题10.1】如图10.3所示，各细长压杆的材料和截面均相同，试问哪根杆能承受的压力最大？哪一根最小？

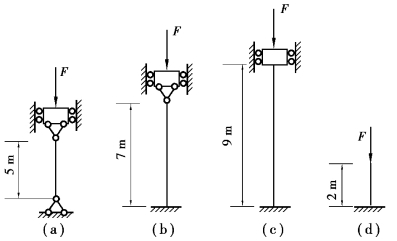
图10.3　习题10.1图

【解】在材料、截面均相同的条件下，对于细长压杆的承载能力，由欧拉公式可知，柔度越大的杆，承载力越小，因此，只需比较各杆的柔度。

（a）杆两端铰支，长度因数μ=1，杆长l=5m，。

（b）杆一端固定，一端铰支，长度因数μ≈0.7，杆长l=7m，。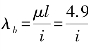

（c）杆两端固定，长度因数μ=0.5，杆长l=9m，。

（d）杆一端固定，一端自由，长度因数μ=2，杆长l=2m，。

由于λa>λb>λc>λd，所以（d）杆能承受的压力最大，（a）杆能承受的压力最小。

【习题10.2】试用欧拉公式计算下列细长压杆的临界压力。杆件两端均为球铰支座，弹性模量均为E=200GPa。

（a）圆截面，d=40mm，l=2.0 m。

（b）矩形截面，h=2b=40mm，l=1.0 m。

（c）No.20a工字钢，l=2.0 m。

【解】（a）解：两端铰支，长度因数μ=1，杆长l=2m。

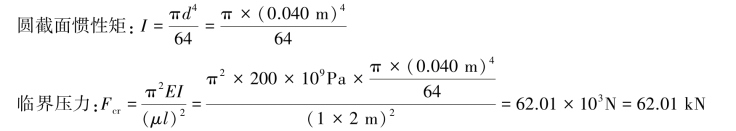
（b）解：两端铰支，长度因数μ=1，杆长l=1m。

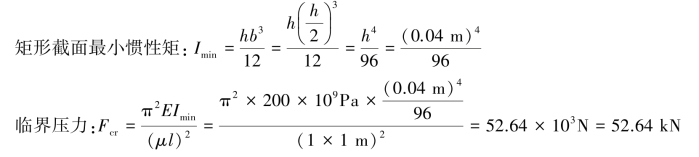
（c）解：两端铰支，长度因数μ=1，杆长l=2m，对于No.20a工字钢，查表知截面最小惯性矩Imin=158cm4=158×10-8m4。

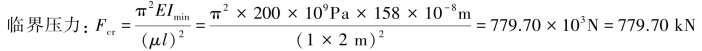
【习题10.3】如图10.4所示，移动式起重机的起重臂AB长l=5.6m，截面外径D=115mm，内径d=105mm，材料为Q235钢，弹性模量E=206GPa，试求起重臂能承受的最大压力。

【解】对于起重臂AB，两端铰支，长度因数μ=1，杆长l=5.6m，横截面的惯性半径为：

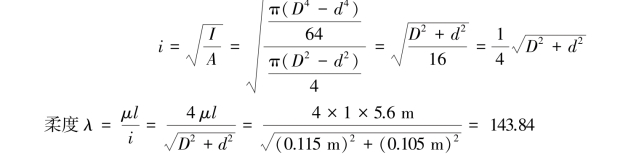
对于Q235钢，有λp=100。因为λ>λp=100，故此起重臂AB为大柔度杆，可采用欧拉公式计算其临界压力：

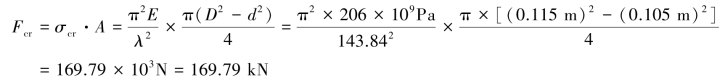
因此，该起重臂能承受的最大压力即临界压力169.79kN。

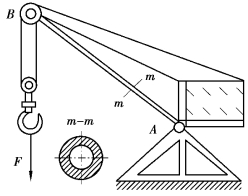
　图10.4　习题10.3图

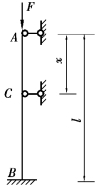
图10.5　习题10.4图

【习题10.4】为了提高如图10.5所示压杆AB的承载能力，欲增加一支座C，问支座C最合适的位置x为多少？增加支座C后，假如AC、BC仍为细长杆，则此时的承载能力是不加支座C时的多少倍？

【解】对于细长压杆AB，增加支座C时，则变成了两个细长压杆AC和CB。

对于细长压杆AC，长度因数μ=1，杆长为x，采用欧拉公式计算其临界压力，有：

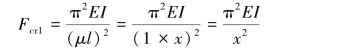
对于细长压杆CB，长度因数μ=0.7，杆长为l-x，采用欧拉公式计算其临界压力，有：

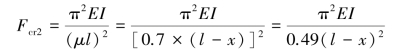
对于整体而言，要求临界压力取上述两者的最小值，而为确定支座C的最合适位置x，则要求上述两者的临界压力值相等，即

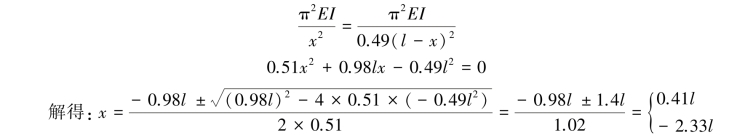
依照题意取x=0.41l。

此时，压杆整体承受的临界压力与局部两杆承受的临界压力相等，为。

而对于细长压杆AB，无支座C时，长度因数μ=0.7，杆长为l，采用欧拉公式计算其临界压力，有：

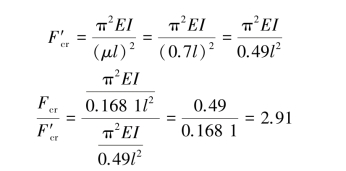
因此，增加支座C后的承载能力是不加支座C时的承载能力的2.91倍。

【习题10.5】截面为100mm×150mm的矩形木柱，一端固定，另一端铰支，杆长l=5.0 m，材料的弹性模量E=10GPa，λp=110。试求此木柱的临界压力。

【解】设矩形截面宽度为b=100mm，高度为h=150mm，截面的惯性矩为I=Ai2，惯性半径为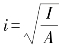，最小惯性半径为。

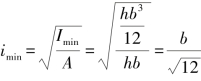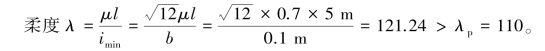
因为λ>λp，则此木柱的临界压力可采用欧拉公式求得：

【习题10.6】如图10.6所示的矩形截面立柱，下端固定，上端承受通过销轴传递的压力F，上端在垂直于销轴的平面内可绕销轴转动，在与销轴平行的平面内由于上部刚性约束不能转动。若要求立柱具有最合理的抵抗失稳的能力，试确定立柱横截面h和b的比值。

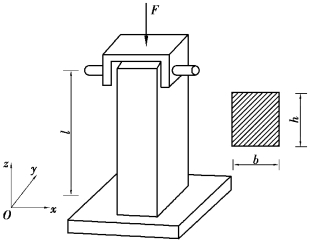
图10.6　习题10.6图

【解】此立柱在垂直于销轴的平面Oyz内可简化为一端固定、一端铰支的细长压杆，长度因数μ=0.7，杆长l，应用欧拉公式计算临界压力，有：

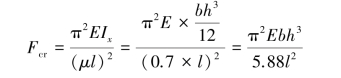
此立柱在平行于销轴的平面Oxz内则可简化为两端固定的压杆，长度因数μ=0.5，杆长l，应用欧拉公式计算临界压力，有：

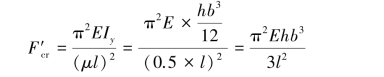
若要求立柱具有最合理的抵抗失稳的能力，则Fcr=F′cr，即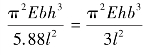：从而解得：

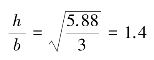
【习题10.7】如图10.7所示为某型飞机起落架中承受轴向压力的斜撑杆。杆为空心圆管，外径D=52mm，内径d=44mm，l=950mm，σb=1600MPa，σp=1200MPa，E=210GPa。试求斜撑杆的临界压力F。

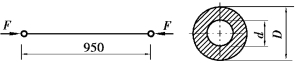
图10.7　习题10.7图

【解】将此斜撑杆简化为两端铰支的压杆，长度因数μ=1，杆长l=950mm，

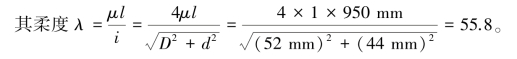
而对于此种材料，有。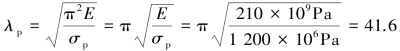

因为λ>λp，则此斜撑杆为大柔度杆，应用欧拉公式计算临界压力，有：

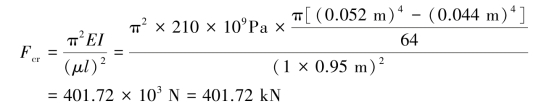
【习题10.8】如图10.8所示，刚性梁ABCD由两根材料相同，半径分别为r、2r的大柔度圆杆支撑，材料的弹性模量为E，试计算荷载F的临界值。

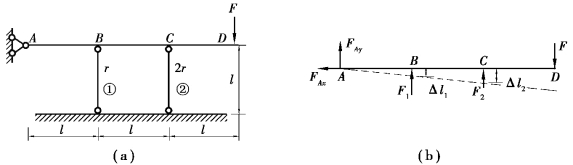
图10.8　习题10.8图

【解】依题意可知，①②两细长杆均受压，其压力分别为F1、F2，对刚性杆AD进行受力分析，如图1.8（b）所示。

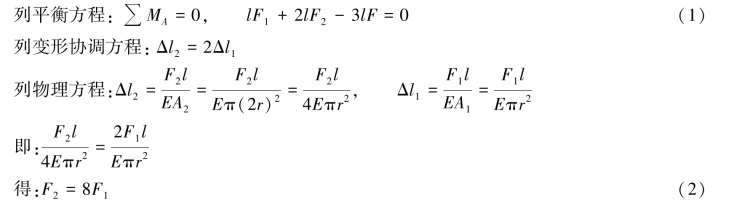
联立式（1）、式（2）解得：。

因为两细长杆均为大柔度杆，且两端铰支，其临界压力可以由欧拉公式计算得到，于是有

【习题10.9】如图10.9所示为两端固定的钢管，外径D=10cm，内径d=8cm，弹性模量E=210GPa，σp=200MPa，热膨胀系数α=12.5×10-6℃-1，钢管长度l=7 m，求钢管不失稳所允许的升温。

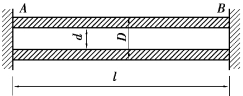
图10.9　习题10.9图

【解】此钢管可简化为两端固支的受压杆件，长度因数μ=0.5，杆长l=7m，其实际柔度为：

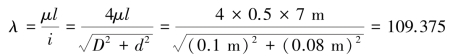
而对于钢管材料，有：

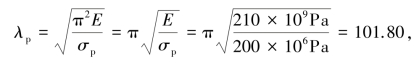
因为λ>λp，则此钢管为大柔度压杆，可应用欧拉公式计算临界应力，有。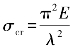

设温度增加ΔT，则结构内产生的温度应力为σt=Eεt=E·αΔT，

令σt≤σcr，则E·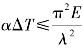

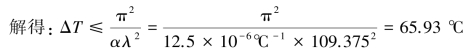
因此，钢管不失稳所允许的最大升温为65.93℃。

【习题10.10】如图10.10所示工字钢直杆在温度T=20℃时安装，此时杆不受力。已知杆长度l=8 m，材料为Q235钢，E=200GPa，线膨胀系数ɑ=12.5×10-6℃-1，当温度升高到多少摄氏度时，杆件将失稳？

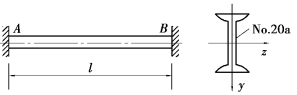
图10.10　习题10.10图

【解】设温度升高引起杆的伸长量为：Δl1=αlΔT，其中ΔT=T2-T1，T1=20℃。

此直杆两端固定，为超静定结构，由固定端处的约束力所引起的杆的缩短量为：。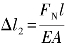

因为杆的总变形量为零，所以有Δl1=Δl2，于是得：FN=EAαΔT。

杆的长度因数μ=0.5，对于No.20a工字钢直杆，查表可知其截面的最小惯性半径imin=2.12cm，最小惯性矩Imin=158cm4，截面面积A=35.578cm2，于是可求得杆的最大柔度为：

对于Q235钢，λp=100，而λmax>λp，故其为大柔度杆，其临界压力可由欧拉公式Fcr=计算求得。

随着温度的升高，轴力FN将逐渐增大，当FN增至Fcr时，杆件将发生失稳，则由，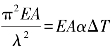

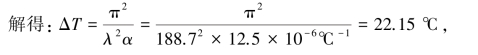
于是可求得：T2=T1+ΔT=20℃+22.15℃=42.15℃。

因此，当温度升高到42.15℃时，杆件将失稳。

【习题10.11】如图10.11所示蒸汽机的活塞杆AB，所受的压力F=120kN，l=1 800mm，横截面为圆形，直径d=75mm。材料弹性模量E=210GPa，比例极限σp=240MPa，要求稳定安全因数nst=8，试校核活塞杆的稳定性。

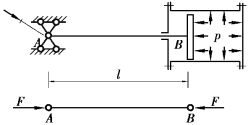
图10.11　习题10.11图

【解】将此活塞杆简化为两端铰支的压杆，长度因数μ=1，杆长l=1.8m，

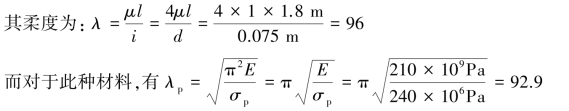
λ>λp，则此杆为大柔度杆，应用欧拉公式计算临界压力，有：

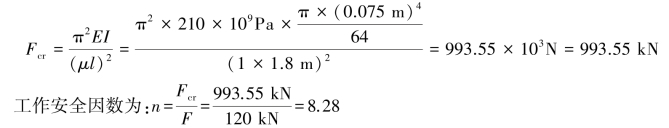
n=8.28>nst=8，工作安全因数大于稳定安全因数，故活塞杆满足稳定性要求，安全。

【习题10.12】平面磨床的工作台液压驱动装置如图10.12所示。油缸活塞直径D=65mm，油压p=1.2MPa，活塞杆长度l=1250mm，材料的E=210GPa，σp=220 MPa，nst=6。活塞杆可简化为两端铰支的压杆，试确定活塞杆的直径。

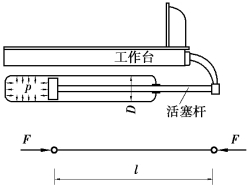
图10.12　习题10.12图

【解】活塞杆受到的压力为：

活塞杆的临界压力为：

(www.xing528.com)

根据已知条件，有。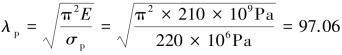

假设此活塞杆为大柔度杆，即λ>λp，则由欧拉公式，有，

其中，μ=1，l=1.25m，。于是，可求得活塞杆的直径为：

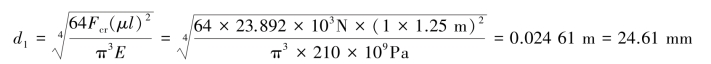
取d1=25mm，再计算压杆的柔度λ，得：

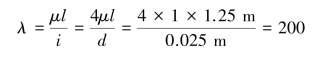
λ>λp，假设成立，于是可确定此活塞杆的直径为25mm。

【习题10.13】如图10.13所示，螺旋千斤顶丝杠的最大承载力F=150kN，直径d=52mm，最大升高长度l=500mm，材料为Q235钢。可以认为丝杠下端是固定的，上端是自由的。试计算丝杠的工作安全因数。

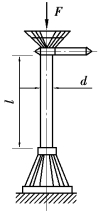
图10.13　习题10.13图

【解】将千斤顶丝杠简化为一端固定，一端自由的压杆，长度因数μ=2，杆长l=0.5m，

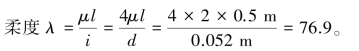
对于Q235钢，λp=100，λs=61.6，因此，此丝杠为中柔度杆。选用直线经验公式计算其临界压力，其中，a=304MPa，b=1.12MPa，得：

若采用抛物线经验公式，则对于Q235钢，有σs=235MPa，E=206GPa，

【习题10.14】如图10.14所示结构，BC为圆截面杆，直径d=80mm，AC为边长a=70mm的正方形截面杆，A端固定，B、C为球铰。两杆均为Q235钢，弹性模量E=210GPa，σp=200MPa，可各自独立发生弯曲，互不影响。若结构的稳定安全因数nst=2.5，求结构的许可压力F。

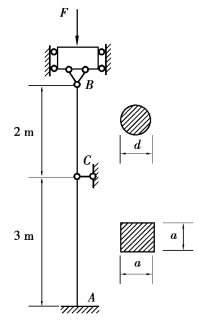
图10.14　习题10.14图

【解】对于杆AC，长度因数μ=0.7，杆长l=3m，其柔度为：

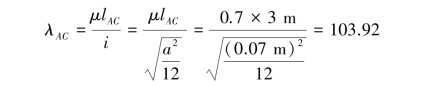
对于杆BC，长度因数μ=1，杆长l=2m，其柔度为：

而对于杆件材料Q235钢，有：

因为λAC>λp，所以杆AC为大柔度压杆，可应用欧拉公式计算杆AC的临界压力，又因为结构的稳定安全因数，所以由杆AC确定的结构的许可压力为：

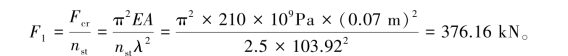
对于杆BC，因为λBC≈λp，可近似认为杆BC也是大柔度压杆。同理，可用欧拉公式计算杆BC的临界压力，再根据结构的稳定安全因数，算得由杆BC确定的结构的许可压力为：

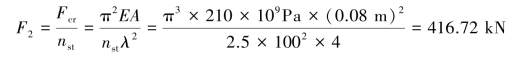
所以，结构最终的许可压力为F=376.16kN。

【习题10.15】一圆木柱高l=6m，直径d=200mm，两端铰支，承受轴向压力F=50kN，试校核其稳定性。已知木材为南方松木TC15，其许用应力[σ]=10MPa。

【解】采用稳定因数法求解。此圆木柱的柔度为：

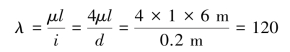
按照强度条件，算得此圆木柱横截面上的工作压应力为：

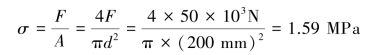
对于南方松木TC15，依据杆的实际柔度查表知其对应的稳定因数φ=0.208，则按照稳定条件折减后的许用应力为：

因为σ<φ[σ]，故该木柱满足稳定性要求，安全。

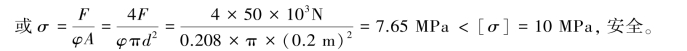
【习题10.16】如图10.15所示截面为工字形的No.40a压杆，材料为Q345钢，许用应力[σ]=230MPa。杆长l=5.6m，在xOz平面失稳时，杆端约束情况接近于两端固定，故长度系数可取为μy=0.65；在xOy平面失稳时为两端铰支，μz=1。试计算压杆所允许承受的轴向压力F。

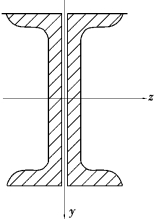
图10.15　习题10.16图

【解】对于No.40a号工字钢，查型钢表知其惯性半径iy=2.77cm，iz=15.9cm，面积A=86.1cm2。两个方向的柔度分别为：

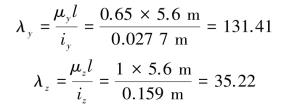
比较柔度λy和λz，取大值来确定折减系数φ。对于Q345类材料，查压杆的稳定因数φ值表（《材料力学》主教材表10.3），采用直线插入法求得

由稳定条件

得压杆允许承受的轴向压力为：

【习题10.17】如图10.16（a）所示托架中，横梁AB承受均布荷载q，CD为直径D=300mm、强度等级为TC15的南方松木杆，其许用应力[σ]=10MPa。试根据CD杆的稳定条件，用稳定因数法求托架的许可荷载q。

【解】求CD杆受到的压力。对横梁AB进行受力分析如图10.16（b），列平衡方程得：

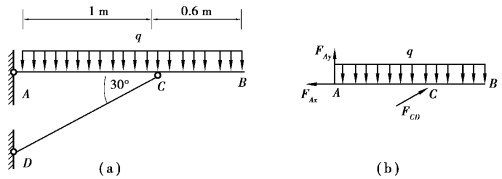
图10.16　习题10.17图

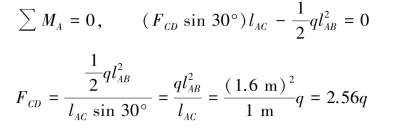
杆CD的长度为：

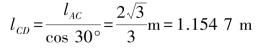
其柔度为：

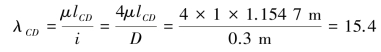
对于强度等级为TC15的松木，查《材料力学》主教材表10.3并采用直线插入法求得

则压杆CD允许承受的轴向压力为FCD=Aφ[σ]。又由FCD=2.56q，得托架的许可荷载为：

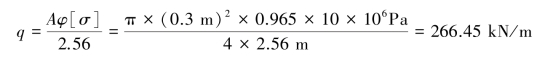
【习题10.18】如图10.17所示结构，AC为矩形截面杆，CD为圆截面杆，材料均为Q235钢，C、D两处为球铰。已知d=20mm，b=100mm，h=180mm，E=200GPa，σp=200MPa，σs=235MPa，强度安全因数n=2.0，稳定安全因数nst=3.3，试确定该结构的许可荷载F。

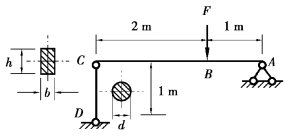
图10.17　习题10.18图

【解】通过受力分析知，杆AC发生弯曲变形，杆CD受压，且。对于杆AC，应按照强度条件确定其许可荷载。

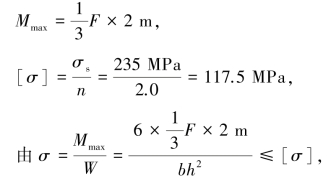
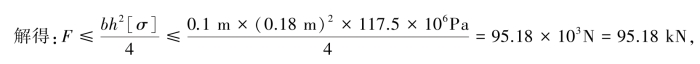
对于压杆CD，其柔度为：

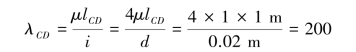
对于杆件材料Q235钢，有：

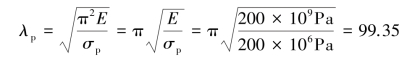
因为λCD>λp，所以杆CD为大柔度压杆，可应用欧拉公式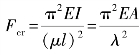计算其临界压力，可根据要求的稳定安全因数确定其许可荷载。

则此结构最终的许可荷载为：F=14.09kN。

【习题10.19】如图10.18（a）所示的三角形桁架，两杆材料均为Q235钢，弹性模量E=200GPa，比例极限σp=200MPa，屈服极限σs=240MPa。已知AB杆的直径d1=40mm，BC杆的直径d2=20mm，F=20kN，强度安全因数n=2.0，稳定安全因数nst=3，试校核结构的安全性。

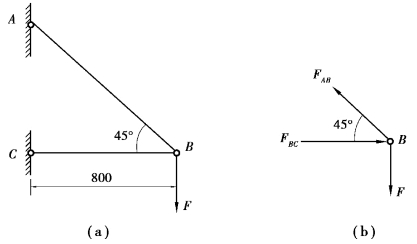
图10.18　习题10.19图

【解】通过受力分析[图10.18（b）]知，杆AB受拉，杆BC受压，且，FBC=F。

对于拉杆AB，应按照强度条件对其安全性进行校核。

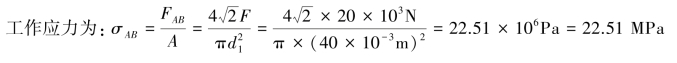
许用应力为：

因为σAB<[σ]，故拉杆AB强度满足要求，安全。

对于压杆BC，其柔度为：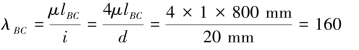

对于杆件材料Q235钢，有：

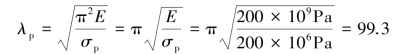
因为λBC>λp，所以杆BC为大柔度压杆，只需满足稳定条件即可。应用欧拉公式Fcr=计算其临界压力，可算得杆BC的工作安全因数为：

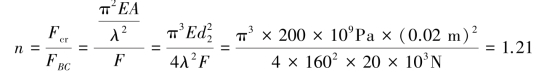
因为n<nst=3.0，故压杆BC稳定性不满足要求，因此该结构稳定性不足，不安全。

【习题10.20】如图10.19（a）所示结构中，横梁AB采用No.16工字钢，立柱CD由两根63mm×63mm×5mm的等边角钢连接而成。材料均为Q235钢，E=200GPa，σs=240MPa，均匀分布荷载集度q=40kN/m。试确定梁与立柱的工作安全因数。

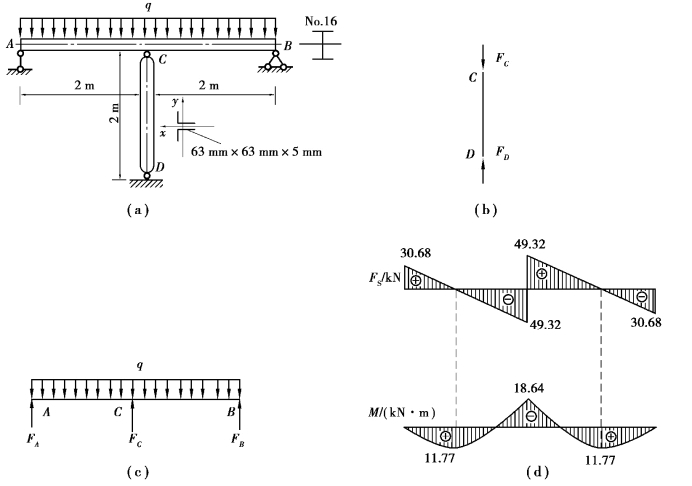
图10.19　习题10.20图

【解】对于No.16号工字钢，查型钢表知：IAB=Ix=1130cm4，WAB=Wx=141cm3。

对于等边角钢63mm×63mm×5mm（两根焊接成一体），有：

（1）计算立柱CD的工作安全因数。对于梁AB，设C点处的位移为fC，有：

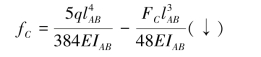
对于立柱CD，设其轴向变形量设为Δl，则有

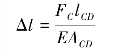
令lAB=l，由题意知，因为fC=Δl，于是可得：

立柱CD的柔度为：

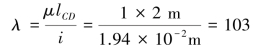
对于Q235钢，λp=100。因为λ>λp，故立柱CD为大柔度杆，其临界压力为：

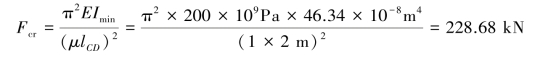
立柱CD的工作安全因数：

（2）计算梁AB的工作安全因数。梁AB的受力如图10.19（c）所示，由对称性可知FA=FB，而FA+FB+FC-ql=0，于是得：

根据梁AB的受力条件，画出其剪力图和弯矩图，如图10.19（d）所示，其最大弯矩为：|M|max=|MC|=18.64kN·m