电解电容器及其种类解析

【习题8.1】试用解析法求图8.3所示各单元体斜截面ab上的应力。应力单位为MPa。

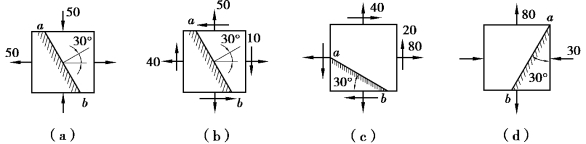
图8.3　习题8.1图

【解】（a）解：依题意知σx=50MPa，σy=-50MPa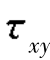，=0MPa，α=30°，由式（8.1）和式（8.2）可得

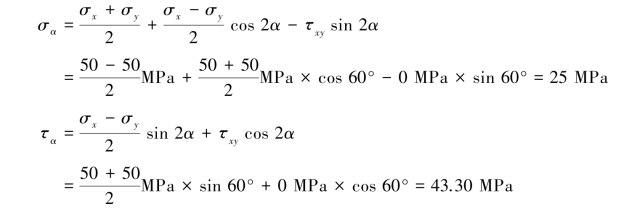
故该单元体斜截面ab上的应力为σ30°=25MPa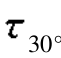，=43.30MPa。

题（b）、（c）、（d）的解题方法同题（a），在此不做详细计算，只给出计算结果。

（b）解：σx=40MPa，σy=50MPa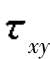，=10MPa，α=30°，由式（8.1）和式（8.2）可得σ30°=33.84 MPa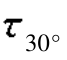=0.67MPa。

（c）解：σx=80MPa，σy=40MPa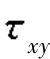，=-20MPa，α=60°，由式（8.1）和式（8.2）可得σ60°=67.32 MPa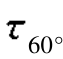，=27.32MPa。

（d）解：σx=-30MPa，σy=80MPa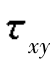，=0，α=150°，由式（8.1）和式（8.2）可得σ150°=-2.5MPa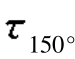，=47.63MPa。

【习题8.2】试用解析法求图8.4所示各单元体的主应力及主平面的方位。应力单位为MPa。

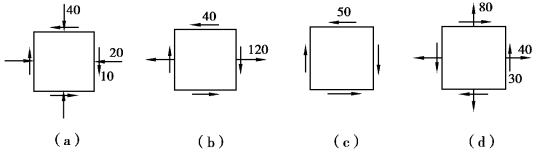
图8.4　习题8.2图

【解】（a）依题意知：σx=-20MPa，σy=-40MPa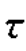，xy=10MPa，由式（8.3）得

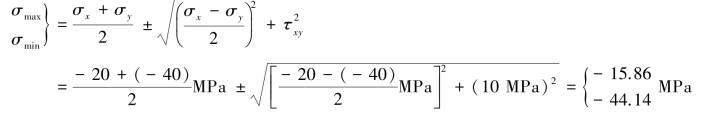
所以主应力为：σ1=0，σ2=-15.86MPa，σ3=-44.14MPa

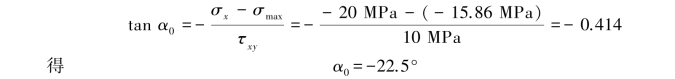
α0即是主应力σ2与x轴的夹角，主应力σ3与x轴的夹角为90°-22.5°=67.5°。

最大切应力为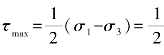：[0MPa-（-44.14MPa）]=22.07MPa

题（b）、（c）、（d）的解题方法同题（a），在此不作详细计算，只给出计算结果。

（b）σx=120MPa，σy=0MPa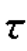，xy=40MPa，解得

（c）σx=0，σy=0MPa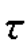，xy=50MPa，解得

（d）σx=40MPa，σy=80MPa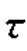，xy=-30MPa，解得

【习题8.3】如图8.5（a）所示，已知矩形截面梁某截面上的弯矩及剪力分别为M=20kN·m，FS=60kN，试绘出截面上1，2，3，4各点的应力单元体，并求各点的主应力。

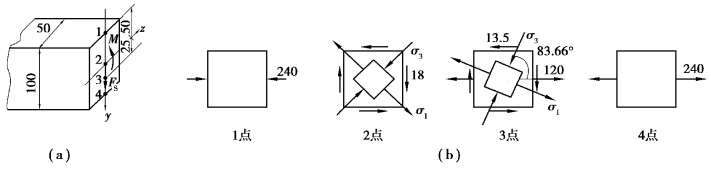
图8.5　习题8.3图

【解】1点：

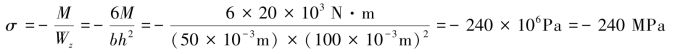
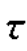=0，为单向压缩应力状态。

主应力为：σ1=σ2=0，σ3=-240MPa。

2点：

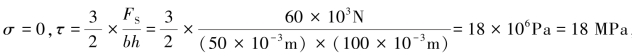，为纯剪切应力状态，属于二向应力状态。

主应力为：σ1=18MPa，σ2=0，σ3=-18MPa。

3点：

4点：

主应力为：σ1=240MPa，σ2=σ3=0

各点的应力单元体如图8.5（b）所示，图中应力单位为MPa。

【习题8.4】一焊接钢板梁的尺寸及受力情况如图8.6（a）所示，梁的自重忽略不计。试求图示C右侧截面上a，b，c三点处的主应力。

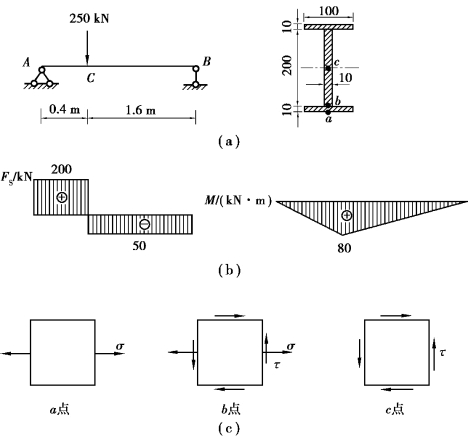
图8.6　习题8.4图

【解】（1）作出梁的剪力图和弯矩图，如图8.6（b）所示，相应的应力单元体如图8.6（c）所示。

在C右侧截面上，FS=-50kN，M=80kN·m。

（2）计算C右侧截面上a，b，c三点处的主应力，设b=100mm，h=220mm，b*=90mm，h*=200mm，于是有

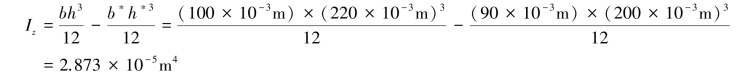
对于点a，有：

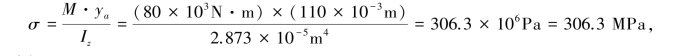
则有σ1=306.3MPa，σ2=σ3=0

对于点b，有：

对于点c，有：

【习题8.5】试用图解法求习题8.1图中各单元体斜截面ab上的应力。

【解】（a）解：由题意可知，σx=50MPa，σy=50MPa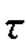，xy=0。按比例建立σ-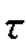坐标系，在该坐标系上，由σx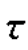，xy确定点A（50，0），由σy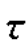，-xy确定点B（-50，0）。应力圆圆心坐标σC=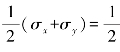（50-50）=0，即为C（0，0），与坐标原点O重合，半径为=50。单元体上斜截面ab的方位角为30°，应力圆上与之对应的点D的圆心角∠AOD=60°，由几何关系知：

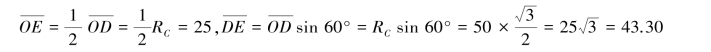
于是可得D点坐标为：D（25，43.30）。

因此，该单元体斜截面ab上的应力：σ30°=25MPa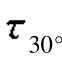，=43.30MPa。

题（b）、（c）、（d）的解题方法同题（a），相对应的应力圆和其斜面ab在应力圆上的点D坐标值如图8.7所示。

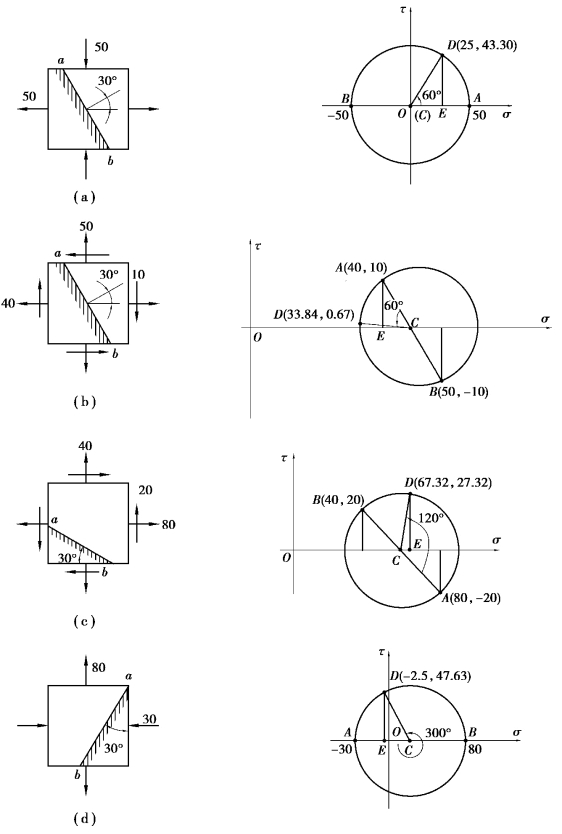
图8.7　习题8.5图

【习题8.6】试用图解法求习题8.2图中各单元体的主应力及主平面，并标注在单元体上。

【解】（a）解：由题意可知，σx=-20MPa，σy=-40MPa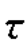，xy=10MPa。按比例建立σ-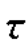坐标系，在该坐标系上，由σx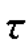，xy确定点A（-20，0），由σy-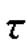xy确定点B（-40，-10），AB连接与σ轴交点C即为圆心，以C点到A点距离为半径画应力圆。应力圆圆心坐标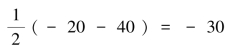，即为C（-30，0），半径为。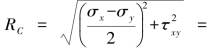

所以主应力为：MPa=-15.86MPa，=-44.14MPa

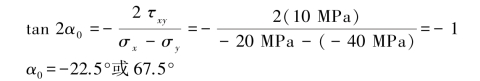
由于xy>0，故α0=-22.5°面上作用的是σ2。在单元体上从水平向右的x轴方向按逆时针方向转过67.5°，确定σ3所在的主平面；按顺时针方向转过22.5°，确定σ2所在的另一主平面，垂直于xy平面的方向，确定σ1所在的主平面。

最大切应力为：

题（b）、（c）、（d）的解题方法同题（a），相对应的应力圆和应力单元体如图8.8所示。

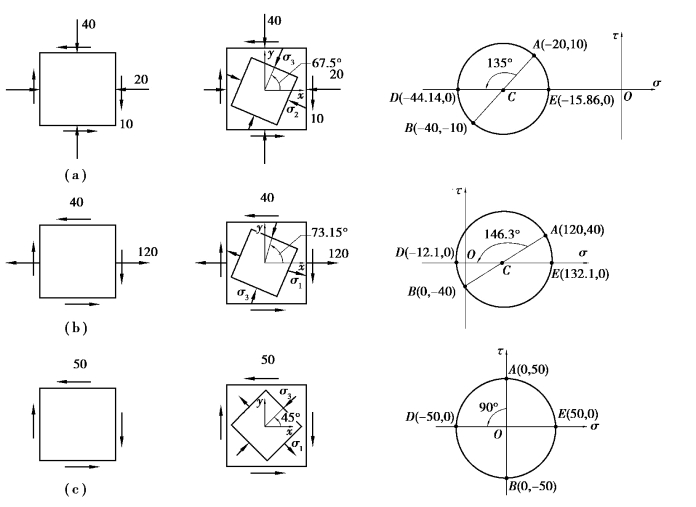
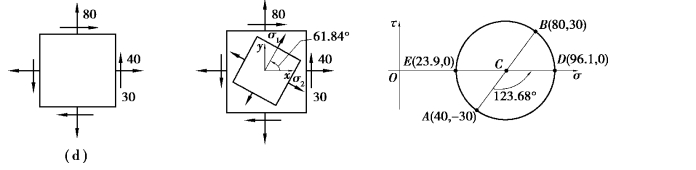
图8.8　习题8.6图

【习题8.7】如图8.9（a）所示的单元体为二向应力状态，应力单位为MPa。试求主应力及主单元体，并作应力圆。

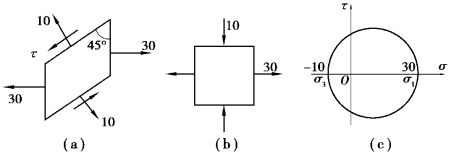
图8.9　习题8.7图

【解】依题意可知：σx=30MPa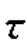，xy=0，α=135°，σα=σ135°=10MPa

由式（8.1）有：，代入已知条件，得

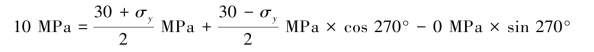
解得：σy=-10MPa

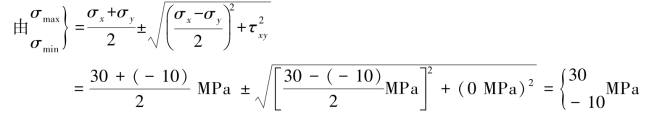
于是有：σ1=30MPa，σ2=0MPa，σ3=-10MPa，该点的主单元体和应力圆如图8.9（b）、（c）所示。

【习题8.8】从构件中取出的微单元受力图如图8.10所示，AC为自由表面（无外力作用）。试求σx和。

【解】对于AC自由表面，依题意可知其方位角α=30°，因此有σ30°=0MPa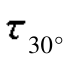，=0MPa，又知：σy=120MPa，由式（8.1）和式（8.2）有

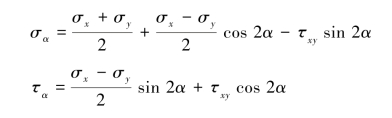
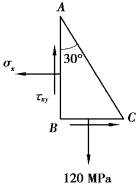
图8.10　习题8.8图

代入已知条件，有

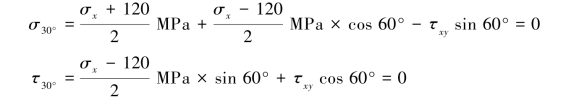
解得：

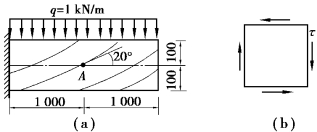
图8.11　习题8.9图

【习题8.9】木质矩形悬臂梁高度为200mm，宽度为40mm，如图8.11（a）所示。在A点木纤维与水平线的倾角为20°。求通过A点沿纤维方向的斜面上的正应力和切应力。

【解】通过A点的横截面上的剪力FSA=1kN/m×1m=1kN横截面上A点处的切应力为

由于点A位于横截面的中性轴上，故横截面上A点处的正应力为0。围绕A点所取单元体为纯剪切应力状态（图8.11（b）），此时的切应力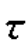=0.1875MPa。通过A点沿纤维方向的斜面的方位角α=110°，由式（8.1）和式（8.2）计算此斜面上的正应力和切应力，得

【习题8.10】试求如图8.12所示各单元体的主应力及最大切应力。图中应力单位均为MPa。

图8.12　习题8.10图

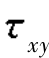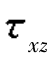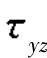【解】（a）σx=0MPa，σy=0MPa，σz=100MPa，=-60MPa，=0，=0

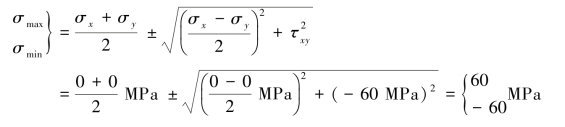
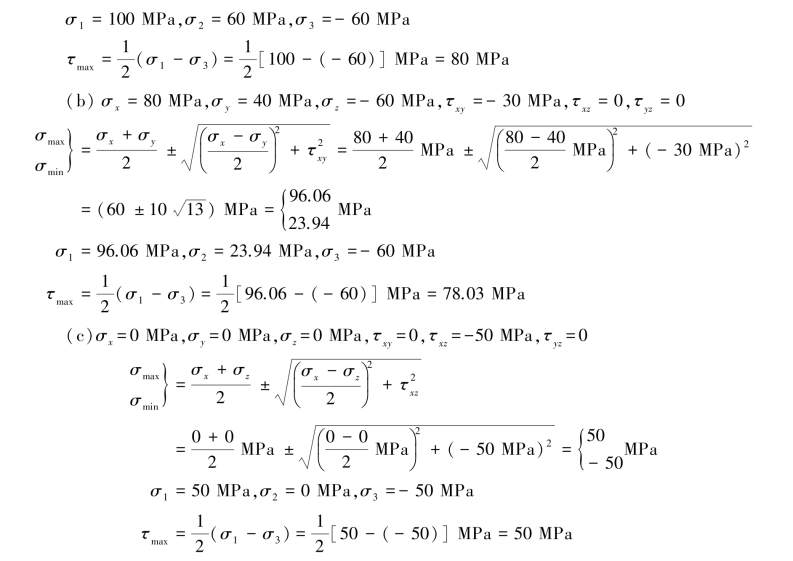
【习题8.11】如图8.13所示矩形截面钢杆在受轴向拉力F=20kN时，测得试样中段B点处与其轴线成-30°方向的线应变ε-30°=3.25×10-4。已知材料的弹性模量E=210GPa，试求泊松比。

图8.13　习题8.11图

【解】如图建立坐标系，得

由广义胡克定律，可得(www.xing528.com)

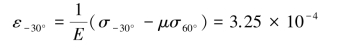
即

则泊松比μ=0.27

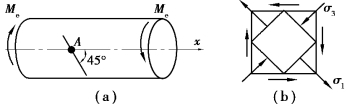
图8.14　习题8.12图

【习题8.12】如图8.14（a）所示的实心圆轴，直径d=20mm，在轴的两端加扭矩Me=126N·m。在轴的表面上某一点A处用变形仪测出与轴线成-45°方向的应变ε=5.0×10-4，试求此圆轴材料的剪切弹性模量G。

【解】A点处于纯剪切应力状态，其应力单元体如图8.14（b）所示。由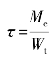，求得：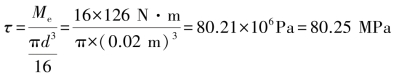

故σ1=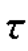，σ2=0，σ3=-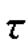，又已知：ε-45°=ε1=5.0×10-4

根据广义胡克定律，有

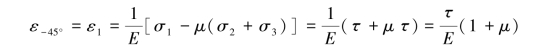
而，所以有：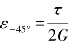

最后得：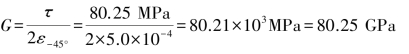

【习题8.13】在平面应力状态下，设已知平面内最大切应变γ=5×10-4，并已知两个互相垂直方向上的正应力之和为27.5MPa。材料的泊松比为μ=0.25，E=200GPa，试计算主应力的大小。（提示：σα+σα+90°=σx+σy=σmax+σmin）

【解】

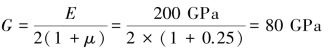
解得：σmax=53.75MPa，σmin=-26.25MPa

故主应力为：σ1=53.75MPa，σ2=0，σ3=-26.25MPa

【习题8.14】如图8.15（a）所示，在一厚钢板上挖了一个尺寸为10mm×10mm×10mm的孔穴，在孔内紧密无隙地嵌入一铝质立方块。若铝块受有合力为F=7kN的均布压力作用，试求铝块的体积变化量。假设厚钢板为刚体，铝立方块的泊松比为μ=0.3，弹性模量E=200GPa。

【解】由题意可知，铝块的应变为：εz=εx=0，zx=0

铝块横截面上的压应力为：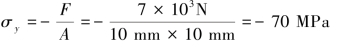

由广义胡克定律有

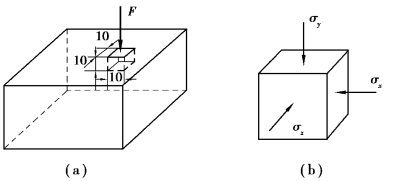
图8.15　习题8.14图

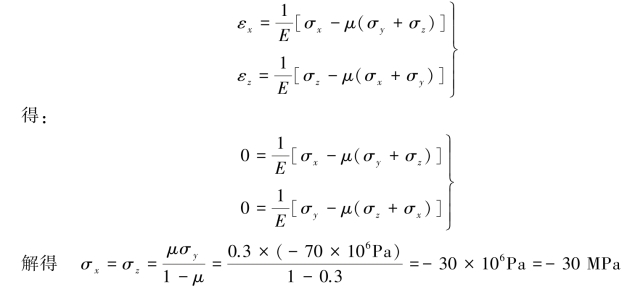
此时的x、y、z三个方向即为主方向，故有：σ1=σ2=-30MPa，σ3=-70MPa

铝块的体积应变为：

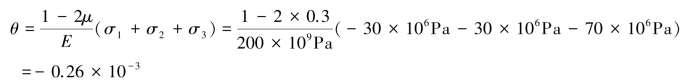
铝块的体积变化量为：

【习题8.15】直径D=40mm的铝质圆柱体，放置到一个厚度δ=2mm的钢套筒内，二者之间无间隙，圆柱受有压力F=40kN，如图8.16（a）所示。若铝的弹性模量E1=70GPa，泊松比μ=0.35，钢的弹性模量E2=210GPa，试求铝圆柱体与钢套之间的挤压力p。

【解】设铝圆柱和钢圆筒之间的挤压力为p，圆柱体内各点均处于三向应力状态。因为径向应变和切向应变相等，则径向应力和切向应力相等，可得到σr=σt=p。

轴向应力为：

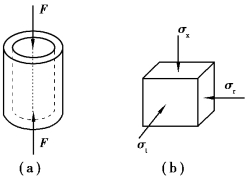
图8.16　习题8.15图

径向应变：

切向应变：

铝圆柱边缘上各点的应力状态单元体如图8.16（b）所示，则由广义胡克定律有：

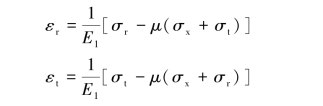
由εr=εt得σr=σt=-p，于是得铝圆柱边缘上各点的切向应变为

铝圆柱周长的改变量为

而钢套可近似的看作薄壁圆筒受径向压力p作用，其径向应力σr′、轴向应力σx′和切向应力为：

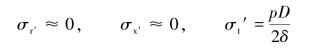
切向应变为：

筒内壁周长改变量为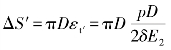

铝圆柱周长和钢套内圆周长改变量相同（即ΔS=ΔS′），有

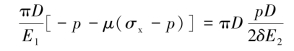
将数值代入上式可求得：p=2.80MPa。

因此，铝圆柱体与钢套之间挤压应力为：p=2.80MPa

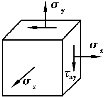
图8.17　习题8.16图

【习题8.16】构件中危险点的应力状态如图8.17所示，试对以下两种情况进行强度校核：

①构件材料为钢材，σx=45MPa，σy=135MPa，σz=0，=0，[σ]=160MPa。

②构件材料为铸铁，σx=20MPa，σy=-25MPa，σz=30MPa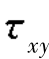，=0，[σ]=30MPa。

【解】（1）由题意可知：σ1=135MPa，σ2=45MPa，σ3=0

因为构件为钢制，属塑性材料，根据第三强度理论，有：

根据第四强度理论，有：

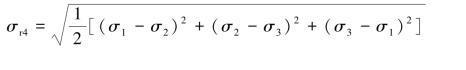
故安全。

（2）由题意可知：σ1=30MPa，σ2=20MPa，σ3=-25MPa

因为构件材料为铸铁，属脆性材料，根据第一强度理论，有：

【习题8.17】某铸铁构件危险点的应力状态如图8.18所示，已知铸铁的许用拉应力[σt]=30MPa，许用压应力[σc]=90MPa，泊松比μ=0.25，试校核该构件的强度。

【解】由题意可知：σx=20MPa，σy=0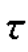，xy=-20MPa

图8.18　习题8.17图

因为构件材料为铸铁，属脆性材料，根据第一强度理论，有：σr1=σ1=32.36MPa>[σt]=30MPa，而且。

【习题8.18】薄壁钢圆筒受最大内压时，测得εx=1.88×10-4，εy=7.37×10-4，如图8.19所示。已知钢的E=210GPa，[σ]=170MPa，泊松比μ=0.3，试用第四强度理论校核其强度。

【解】薄壁圆筒上的点可简化为平面应力状态，则由广义胡克定律得：

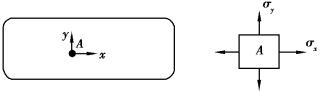
图8.19　习题8.18图

于是得：σ1=183.09MPa，σ2=94.41MPa，σ3=0

根据第四强度理论，有：

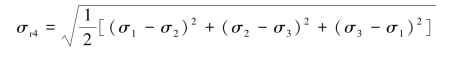
根据第四强度理论，此容器强度足够，故安全。

【习题8.19】某钢制圆柱形薄壁容器，直径D=1000mm，壁厚δ=4mm，[σ]=160MPa。试用第三强度理论确定可能承受的内压力p。

【解】建立坐标系并取分离体（图8.20），有：

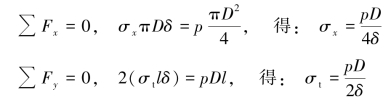
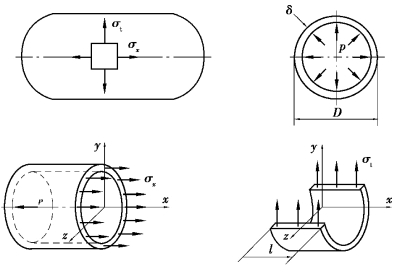
图8.20　习题8.19图

在D≫δ的条件下，p与σt和σx相比很小，可略去不计，故主应力为：

根据第三强度理论，有：

于是解得：

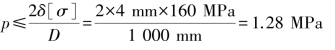
则此钢制圆柱形薄壁容器可能承受的最大内压力p为1.28MPa。

【习题8.20】一简支的NO.28a工字钢梁承受荷载如图8.21（a）所示，已知材料的许用应力[σ]=170MPa，[]=100MPa。试按弯曲正应力强度条件和切应力强度条件校核梁的强度，并校核腹板与翼缘交界处a点的强度。

【解】画此简支梁的内力图如图8.21（b）所示，有：FS，max=200kN，Mmax=80kN·m。

对于NO.28a工字钢，查表知：d=8.5mm，h=280mm，b=122mm，t=13.7mm，Iz=7110cm4，Wz=508cm3，Iz∶Sz=24.6cm。

最大弯曲正应力为：

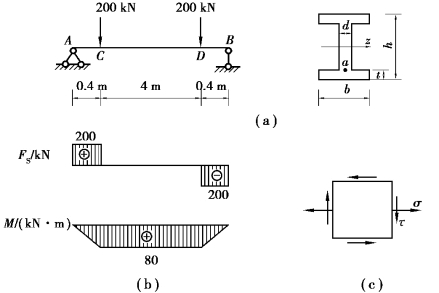
图8.21　习题8.20图

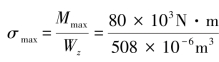=157.48×106Pa=157.48MPa<[σ]=170MPa，故满足弯曲正应力强度条件。

最大弯曲切应力为：

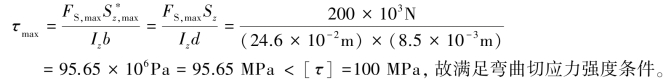
对于危险截面上腹板与翼缘交界处a点，有

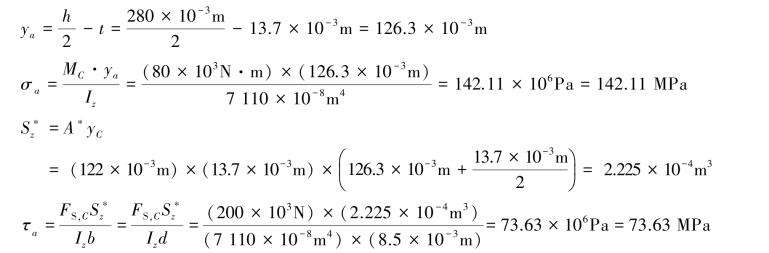
按第三强度理论，有：

按第四强度理论，有：