1)一点处的应力状态
所谓一点处的应力状态,是指受力杆件中任一点处各个截面上所有应力的集合。一般情况下,过同一点的不同截面上的应力是不相同的;同一截面上不同位置的点的应力状态也是不同的。通常用应力单元体和应力圆来描述一点的应力状态。
2)主应力和主平面
单元体上切应力为零的面称为主平面,主平面上的正应力称为主应力。构件中的任何一点都存在三个相互垂直的主平面,对应的三个主应力也是相互垂直的。最大主应力σ1和最小主应力σ3分别是构件中某点处的最大正应力和最小正应力。在该点其他任何方位的截面上的正应力数值一定都在σ1和σ3之间。
3)应力状态分类
根据三个主应力σ1,σ2,σ3的值是否等于零来确定应力状态分类。如果σ1、σ2、σ3均不等于零,则为空间应力状态,其中一个等于零的则为平面应力状态,两个等于零的则为单向应力状态。
4)平面应力状态的分析计算
通常,已知单元体上相互垂直的两个平面上的应力,根据解析法公式可以求任意斜截面上的应力、主应力、主平面、最大切应力等。
(1)斜截面上应力的计算。

(2)主应力和主平面方位的计算。
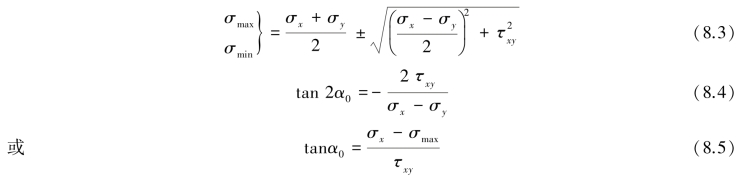
将σmax、σmin和0按大小排序确定主应力σ1,σ2,σ3。
(3)主切应力的计算。
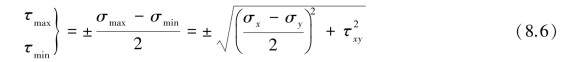
主切应力作用面与主平面之间的夹角为45°。
也可以利用应力圆来求任意斜截面上的应力、主应力、主切应力及其作用面。应力圆上的点与单元体上的面存在一一对应关系,其对应原则为:圆上一点,体上一面;直径两端,垂直两面;点面对应,基准一致,转向相同,转角两倍。(https://www.xing528.com)
5)空间应力状态
单向应力状态、平面应力状态都是空间应力状态的特例,因此,某一点处应力状态的最大、最小正应力和最大切应力应按下式确定:

6)广义胡克定律
广义胡克定律建立了单元体中应力与应变之间的关系,利用这种关系,可以通过已知应力求应变,也可以通过已知应变求应力。

7)强度理论
强度理论是研究材料在复杂应力条件下强度失效的原因和失效条件的理论。脆性断裂和塑性屈服是强度失效的两种基本形式。
(1)最大拉应力理论(第一强度理论):![]()
(2)最大拉应变理论(第二强度理论):![]()
(3)最大切应力理论(第三强度理论):![]()
(4)形状改变比能理论(第四强度理论):
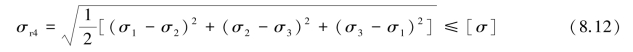
(5)莫尔强度理论:

8)强度理论的适用范围
第一和第二强度理论是用来解释材料的脆性断裂的;第三和第四强度理论是用来解释材料的塑性屈服的。材料强度失效不仅取决于材料的性质,而且还与危险点处的应力状态有关。一般情况下,脆性材料选用脆断的强度理论与莫尔强度理论,塑性材料选用关于屈服的强度理论。无论是塑性还是脆性材料,在三向受拉应力状态下都将以断裂形式失效,宜采用第一强度理论;在三向压应力状态下都将发生塑性屈服,宜采用第三或第四强度理论。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




