MeanShift算法原理详解

均值漂移的基本思想是，对多维空间中的多个变量点计算偏移量的平均值，假设在d 维空间Rd 中总共有n 个样本点，这些样本点用xi (i = 1，2，…，n )表示，它们在点x 的Mean Shift 向量的基本形式可以定义为:

其中，Sh 是一个球区域，h 表示这个球区域的半径，它们满足以下关系:

这是一个表示y 点的集合，k 表示落入球区域Sh 中的点的个数，样本点xi 相对于点x 的偏移向量是 (xi－ x )。式(9.1)定义的向量Mh( x )就是这个偏移向量的求和平均值。

从直观上看，如果这个样本点xi 是从概率密度函数f( x )中采样获取的，计算概率密度时，非零的概率密度梯度会向概率密度增加最大的方向移动，因此，落在区域Sh 内的样本点k 更多的是在概率密度梯度递增的方向上。在空间分布上，式(9.1)表示的向量Mh( x )也应该指向概率密度梯度增大的方向，如图9.1 所示。

图9.1　Mean Shift 示意图(www.xing528.com)

图9.1 中，中心的黑点是Mean Shift 的基准点x，圆圈内的范围就是Sh 表示的球区域，带箭头指向的小圆圈代表落入此区域内的采样样本点xi ，并且有xi ∈Sh ，箭头表示xi 相对于x 的偏移向量所示的方向。由图可知，向量Mh( x )更多地指向概率密度梯度增大的方向。

此外，Mean Shift 算法还可以表示为:

引入窗口宽度函数h 可以增强处理的效益，Mean Shift 算法又可以表示成:

引入权重参数后，Mean Shift 算法表示为:

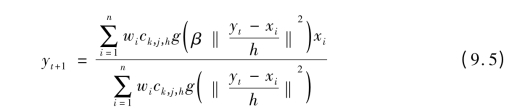
其中，，h 为常数且h ＞0 。