【摘要】:为了适应这个表述,Hf 称之为局部熵。假定目标在位置0 处,背景是均匀的,H9 标示3 ×3 的邻域局部熵。如果去除3 ×3 的邻域中心点,则新的局部图就有相邻点构成。新的局部熵定义为:假定没有目标在均匀的背景中,H9 与H8 近似相等,也就是说,Hz 近似等于零。表5.1空间位置分布标识表5.2空间分布灰度值Hf 是关于pij2 的线性组合。它的加权系数为1。
红外目标检测算法已得到长足发展,但是当遭遇到背景急剧变化时,对于目标的检测就会存在一定问题。假定大小M × N 的图像F = [f(x,y)]M×N ,其中f(x,y)表示空间坐标(x,y)所对应的灰度值。f(x,y)∈GL = {0,1,···,L - 1 },其中GL 表示灰度等级。那么熵定义如下表示:
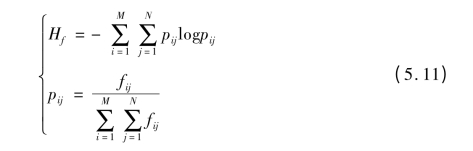
其中Hf 表示图像熵,pij 表示灰度概率。假定M × N 表示图像局部窗的大小,那么Hf 就表示为图像的局部熵。
当采用局部熵检测红外目标,熵的计算近似如下形式:
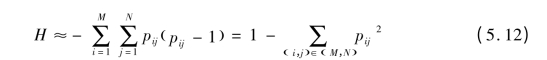
进一步简化表达式为:
![]()
在相对均质化的灰度等级空间,Hf 会成为一个很小值;在大的离散区域,Hf 会成为一个很大值。尽管Hf 反映图像灰度的散差,它与熵描述意义的初始特性恰好相反。为了适应这个表述,Hf 称之为局部熵。
假定目标在位置0 处,背景是均匀的,H9 标示3 ×3 的邻域局部熵。如果去除3 ×3 的邻域中心点,则新的局部图就有相邻点构成。新的局部熵定义为:(https://www.xing528.com)
![]()
假定没有目标在均匀的背景中,H9 与H8 近似相等,也就是说,Hz 近似等于零。但是如果目标位于中心点,由于目标的出现,3 × 3 邻域的离散程度就会增加。将它从中心点剔除,离散程度就会降低。参见表5.1 和5.2 所示。
表5.1 空间位置分布标识
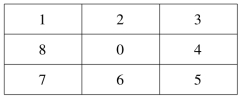
表5.2 空间分布灰度值
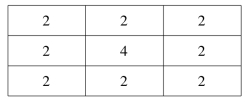
Hf 是关于pij2 的线性组合。它的加权系数为1。重新修正该加权系数,对应中心点,它的加权系数为α,则Hf 表达式变为[106]:
![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




