形状保持的变分模型及其能量泛函

图像在形成、传输、存储过程中，图像质量可能退化。如何恢复图像，运用变分模型是解决问题的方法之一。

(1)全变分模型。

图像中含有噪声是不可避免的。在图像处理中，对于真实信号的估计通常采用最小二乘方准则，其实质是二次范数。但一次范数更适合于图像的恢复。有界全变分函数空间在对图像不连续点的估计扮演着更精确的角色。在进行图像处理任务之前，传统方法都要先抑制噪声，而基于全变分方法的理论可以同时处理图像去噪和其他任务。

被观测函数u0 (x，y )表示在空间坐标(x，y)的图像灰度，u (x，y )表示为理想的无噪声图像。两者可以通过下述表达式联系起来:

其中n 表示加性噪声。

通常希望从u0 中重构u。传统变分方法采用最小二乘方法。其最小化问题为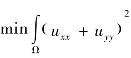，且服从均值约束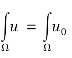与标准方差约束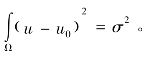上述产生的线性系统很容易采用现代数字线性代数解决，然而其结果却令人失望。在冲击计算中，梯度一次范数是合适空间，它是有界全变差函数空间，突变信号在该空间可以得到有效保护。其最小化问题为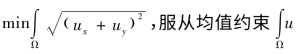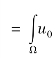与标准方差约束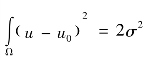。因此上述变为一个线性与一个非线性约束。该方法被称为量与形的约束，并可以转化为欧拉—拉格朗日方程:

变分方法中经典的正则化是Rudin L、Osher S 和Fatemi E 提出的变分极小化方法(R-O-F 模型)［43］，它以作为图像的平滑性度量。与比较，它可以更好地保护图像边缘。其图像去噪的模型如下表示:

R-O-F 模型的欧拉—拉格朗日方程如下:

其最小化J(u)的梯度下降法为:

尽管它具有去噪和图像特征保持的特点，但是方程(3.18)的演化变化不仅取决于它的水平集(由∇u 表征)，同时还取决于它的灰度值u。这一缺陷的直接表现是其稳态解中往往具有明显的阶梯效应［90］。(www.xing528.com)

(2)形状保持的变分模型。

为了鉴别类似拐角目标特征与度量结构的局部一致性，在任何空间观测点，必须考虑到梯度的变化特性。结构张量矩就是一个描述该类特征的量。该矩阵对于分析纹理、拐角与T 连接是非常有用的。在矩阵框架下，结构描述子∇uσ 被引入，张量积的矩阵J0 定义为:

矩阵J0 拥有正交矢量基v1，v2 ，v1‖∇uσ ，v2 ⊥∇uσ 。通过与高斯核Kρ 卷积，矩阵J0 变为:

于是Jρ 成为一个对称矩阵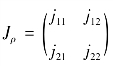，同时它也是一个半正定矩阵。方程(3.20)展开描述:

其中

Chung D H 和Sapiro G (C-S 模型)［46］提出矢量图像的等高线概念，为获取保持形状的图像提供了理论基础。对于给定的图像u，找到图像u，使得它的梯度矢量与给定图像u 的本征矢量v 处处一致。其能量泛函表示如下:

通过运用变分问题所对应的欧拉—拉格朗日方程，利用梯度下降法:

其中定义f(λ1，λ2)与梯度大小|∇u|相等。尽管该模型具有图像形状保持的特征，但是由于噪声所引起的虚假边缘，该模型同样保留其伪边缘，并且图像去噪效果有所欠缺。