非线性扩散模型：扩散过程的物理背景

基于偏微分方法出现在多种图像处理领域，比如图像平滑、图像恢复以及边缘检测。而这些方法的原理源自于物理现象，如波传播或热传送。

(1)扩散过程的物理背景。

许多人对物理现象中由于浓度差异所产生的扩散平衡过程具有强烈的感官印象，该物理现象很容易以数学表达式来描述，其平衡特性以菲克定理来描述:

上述方程说明通过浓度梯度∇u 产生了用于补偿梯度差异的流量j。∇u 与j 的关系通过扩散张量D 来描述，且该张量是正定对称矩阵。当j 与∇u 方向平行时，被称之为各向同性，可通过正标量值的扩散系数g 代替扩散张量。当j 与∇u 方向不平行时，称之为各向异性。扩散现象的观测还可以通过连续性方程来表达:

其中t 表示时间。将菲克定理引入到连续性方程，上述扩散方程变为:

许多物理传送过程都可以用该方程来描述。以热传送为例，它被称为热方程。

(2)线性扩散滤波器。

广泛地平滑灰度图像f 的方法是通过计算卷积，其表达式如下表述:

其中Kσ 表示标准偏差σ 的二维高斯函数。高斯函数方程表示如下:

则线性扩散过程表示如下:

它的唯一解如下表述:

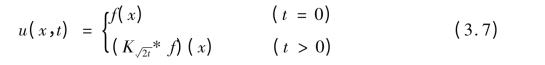(www.xing528.com)

(3)非线性扩散。

非线性扩散方程首先由Perona 和Malik(P-M 模型)［39］提出。对于图像多尺度语义的描述必须满足因果关系、局域关系与分段平滑关系。换句话说就是:真实信号应当满足从精尺度传递到粗尺度空间不会产生新的信号;在任何分辨率下的区域边界应与该分辨率下的语义边界一致;内部区域平滑优先于跨部区域。

以一维信号为例:

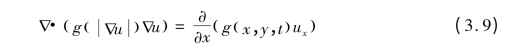
g 视为信号u 的梯度函数。则表达式(3.8)变成:

其中Φ ( ux )= g ( ux ).ux ，g ( ux )= C/ (1 + (　ux/λ　)1+α )。针对特定限值λ、a，当ux 小于λ 时，流量函数Φ 单调递增;当大于λ 时，流量函数Φ 单调递减。通过这些设置，它能够锐化边缘与模糊小的不连续点。令ux = s，具体流量函数、扩散率函数与梯度关系满足图3.1 关系。

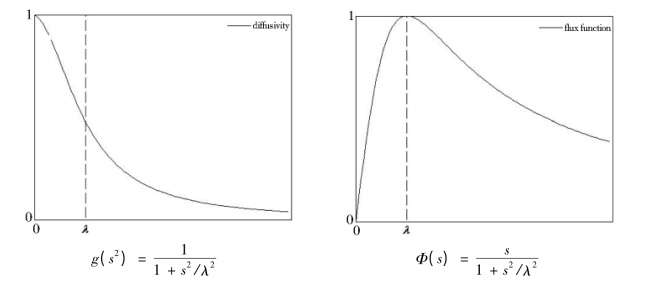
图3.1 扩散率、流量函数与梯度关系

对于二维信号，采用拉普拉斯算子的4 －邻域离散化，表达式(3.8)可以变成如下:

下标N、S、E 与W 依次表示北、南、东与西方向。∇表示邻域差分，也就是梯度算子。∇N、∇S、∇E 与∇W 表达式参见方程(3.12):

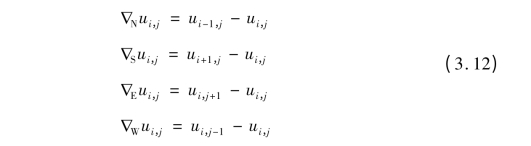
其中g 的定义如下:

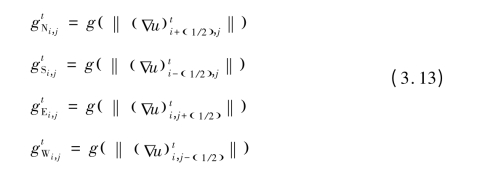
在表达式中，区域扩散优先于区间平滑。传导系数g 是可以设置的。假定每个区域内的传导系数设定为1，而在区域边界，传导系数设定为0，则模糊现象只能发生在每个区域内，而在边界交界处不会产生，所以边缘的边界得以保持。然而传统的低通滤波器和线性扩散在消除噪声的同时，边缘却被模糊。模糊图像的边缘增强与重构可以通过高通滤波器或反向扩散实现，但是它是个病态问题，会带来计算的不稳定性。在图像处理中，扩散张量不是一个常量，而是一个与图像局部结构特征有关的函数，因此产生了非线性扩散滤波器。非线性扩散滤波器包含自适应局部图像结构扩散系数的非线性扩散滤波器及使用自适应局部图像结构扩散张量的非线性各向异性扩散滤波器。在Perona 和Malik 方法中，他们把传导系数视作图像梯度函数。当正向扩散时，各向异性扩散能够增强边缘。当在图像平坦区域的时候，扩散系数大;当在图像突变区域的时候，扩散系数小。这就起到自动保护图像边缘信息和去噪的目的。尽管P-M 模型具有抑制噪声的特性，但是对图像产生阶梯效应、分块效应，破坏了图像的边缘、细节信息。也就是说，它虽然能够抑制噪声，但不能有效地保持空间分辨率。