【摘要】：利用Grumwald-Letnikov 定义在信号的数值实现上更为精确，因而从该定义出发推导分数阶微分算子［85］。表2.113 ×3 Tiansi 模板表2.125 ×5 Tiansi 模板关于图像增强，为防止图像数据溢出，需要对上述模板进行归一化处理。Tiansi 分数阶微分克服整数阶微分的缺陷，不仅一般信号的高频成分得以提升，而且低频信号得以非线性保留，但是该分数阶微分算子抑制噪声能力较弱。
利用Grumwald-Letnikov 定义在信号的数值实现上更为精确，因而从该定义出发推导分数阶微分算子［85］。其表达式如下:
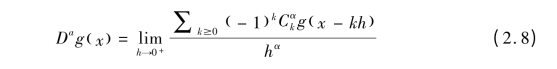
其中g( x )表示实函数，α ＞0 ，
表示广义二项式系数，Γ( x )代表Gamma 函数。当α = 1 且k ≥2 时，表达式(2.8)变为整数一阶微分。对于定值α，当k →∞时，
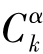快速趋近于零。当我们选择h = 1 时，有限分数阶微分表示如下:
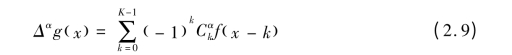
当α = 1 ，方程式(2.9)变为一阶前向差分。
根据Grumwald-Letnikov 分数阶微分定义，一维信号f(t)分数阶微分的差分表达式近似如下:
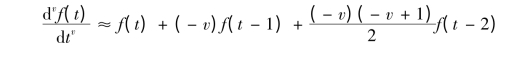(www.xing528.com)
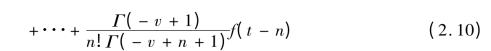
依据上述差分表达式，构建各向同性滤波器［85］。其中v 表示分数阶微分阶数。依次以3 ×3 、5 ×5 模板为例，参见表2.11 与表2.12。
表2.11 3 ×3 Tiansi 模板
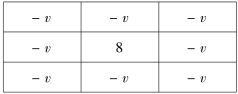
表2.12 5 ×5 Tiansi 模板
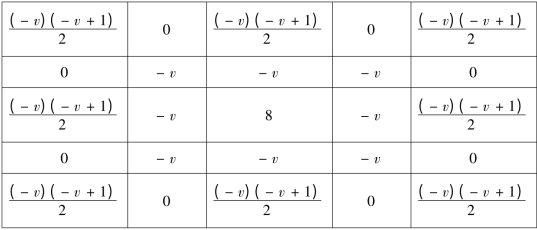
关于图像增强，为防止图像数据溢出，需要对上述模板进行归一化处理。通过设置合理的v，获得模板滤波器，使用滤波器逐次在被处理图像中移动，求得滤波器响应，最终获得图像增强。Tiansi 分数阶微分克服整数阶微分的缺陷，不仅一般信号的高频成分得以提升，而且低频信号得以非线性保留，但是该分数阶微分算子抑制噪声能力较弱。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
