大涡模拟：湍流模拟的新主角

湍流中包含了不同时间与长度尺度的涡旋。最大长度尺度通常为平均流动的特征长度尺度。最小尺度为Komogrov尺度。大涡模拟（LES）的基本假设是：①动量、能量、质量及其他标量主要由大涡输运；②流动的几何和边界条件决定了大涡的特性，而流动特性主要在大涡中体现；③小尺度涡旋受几何和边界条件影响较小，并且各向同性。LES过程中，直接求解大涡、小尺度涡旋模拟，从而使得网格要求比直接数值模拟（DNS）低。

LES的控制方程是对Navier-Stokes方程在波数空间或者物理空间进行过滤得到的。过滤的过程是去掉比过滤宽度或者给定物理宽度小的涡旋，从而得到大涡旋的控制方程：

式中，τ_ij为亚网格应力，。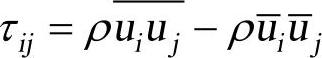

很明显，上述方程与Reynolds平均方程很相似，只不过大涡模拟中的变量是过滤过的量，而非时间平均量，并且湍流应力也不同。(www.xing528.com)

大涡模拟无论从计算机能力和方法的成熟程度来看，离实际应用还有较长距离，但湍流模型方面的研究重点已转向大涡模拟。估计在今后10年内，随着这一方法的成熟以及计算机能力进一步提高，大涡模拟将逐步成为湍流模拟的主要方法。

除了上述各类模型以外，有实用价值的还有改进的单方程模型，它对近壁流的模拟效果较好，以及简化的湍应力模型，即代数应力模型。从实用性来说，它们很有推广价值，尤其是代数应力模型，既能反映湍流的各向非同性，计算量又远小于湍应力模型。