【摘要】：Reynolds应力模型是求解Reynolds应力张量的各个分量的输运方程。在式中，Cij、DijL、Pij、Fij不需要模拟，而Dijr、Gij、Φij、εij需要模拟以封闭方程。浮力引起的产生项Gij模拟为耗散张量εij模拟为式中，YM=2ρεMt2，Mt是马赫数；标量耗散率ε用标准k-ε模型中采用的耗散率输运方程求解。
Reynolds应力模型（RSM）是求解Reynolds应力张量的各个分量的输运方程。具体形式为
式中，左边的第二项是对流项Cij；右边第一项是湍流扩散项Dijr；第二项是分子扩散项DijL；第三项是应力产生项Pij；第四项是浮力产生项Gij；第五项是压力应变项Φij；第六项是耗散项εij；第七项是系统旋转产生项Fij。
在式（7-12）中，Cij、DijL、Pij、Fij不需要模拟，而Dijr、Gij、Φij、εij需要模拟以封闭方程。下面简单对几个需要模拟项进行模拟。
Dijr可以用Delay和Harlow的梯度扩散模型来模拟，但这个模型会导致数值不稳定，在FLUENT软件中是采用标量湍流扩散模型：
式中，湍流粘性系数用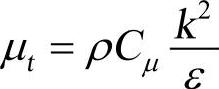
来计算，根据Lien和Leschziner，σk=0.82，这和标准k～ε模型中选取1.0有所不同。
压力应变项Φij可以分解为3项，即(www.xing528.com)
Φij=Φi,j,1+Φij,2+Φijw （7-14）
式中，Φi,j,1、Φij,2和Φijw分别是慢速项、快速项和壁面反射项。
浮力引起的产生项Gij模拟为
耗散张量εij模拟为
式中，YM=2ρεMt2，Mt是马赫数；标量耗散率ε用标准k-ε模型中采用的耗散率输运方程求解。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
