【摘要】:从对模式处理的出发点不同,可将湍流模式理论分为两大类:一类称为雷诺应力模式,另一类称为涡粘性模式。在工程湍流问题中得到广泛应用的模式是涡粘性模式。所有一方程和两方程的湍流模型都可写为如下的一般形式:式中,SP是“产生”源项;SD是“破坏”源项;D表示扩散项,其形式为。
目前处理湍流数值计算问题有3种方法:直接数值模拟(DNS)方法,大涡模拟(LES)方法和雷诺平均N-S方程(RANS)方法。RANS方法是目前唯一能够应用于工程计算的方法。雷诺平均N-S方程方法首先将满足动力学方程的湍流瞬时运动分解为平均运动和脉动运动两部分,然后把脉动运动部分对平均运动的贡献通过雷诺应力项来模化,也就是通过湍流模式来封闭雷诺平均N-S方程使之可以求解。从对模式处理的出发点不同,可将湍流模式理论分为两大类:一类称为雷诺应力模式,另一类称为涡粘性模式。在工程湍流问题中得到广泛应用的模式是涡粘性模式。这是由法国力学家Boussinesq仿照分子粘性的思路提出的,即假设雷诺应力为
式中,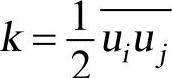 是湍动能;νt称为涡粘性系数。
是湍动能;νt称为涡粘性系数。
这便是基准涡粘性模式,即假设雷诺应力与平均速度应变率呈线性关系,当平均速度应变率确定后,6个雷诺应力只须通过确定一个涡粘性系数νt就可完全确定,且涡粘性系数各向同性,可以通过附加的湍流量来模化,如湍动能k,耗散率ε,比耗散率ω以及其他湍流量τ=k/ε,l=k3/2/ε,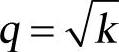 。根据引入湍流量的不同,可以得到不同的涡粘性模式,如k−ε和k−ω模式等。对应不同模式,涡粘性系数可表示为
。根据引入湍流量的不同,可以得到不同的涡粘性模式,如k−ε和k−ω模式等。对应不同模式,涡粘性系数可表示为
为使控制方程封闭,引入多少个附加的湍流量,就要同时求解多少个附加的微分方程。根据要求解的附加微分方程的数目,一般可将涡粘性模式分为3类:零方程和半方程模式、一方程模式、两方程模式。(https://www.xing528.com)
所有一方程和两方程的湍流模型都可写为如下的一般形式:
式中,SP是“产生”源项;SD是“破坏”源项;D表示扩散项,其形式为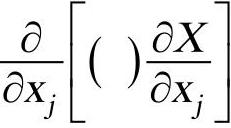 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




