Spark GraphX是在Spark Core上构建的一个子系统,对GraphX视图的所有操作,最终都会转换成其关联的Table视图的RDD操作。这样对一个图的计算,最终在逻辑上等价于一系列的RDD的转换过程。因此,Spark GraphX的属性图最终具备了RDD的三个关键特性:Immutable(不可变性)、Distributed(分布式)和Fault-Tolerance(容错),其中最关键的是Immutable(不可变性)。逻辑上,所有图的转换和操作都产生了一个新图;物理上,Spark GraphX会有一定程度的不变顶点和边的复用优化,对用户透明。
Spark GraphX的代码架构非常简洁,Spark GraphX的核心代码只有3000多行,而在此之上实现的Pregel模型,只要短短20多行。Spark GraphX的代码结构整体如图8-6所示,其中大部分的实现都是围绕Partition(分区)的优化进行的,这在某种程度上说明了点分割的存储和相应的计算优化的确是图计算框架的重点和难点。
对于Graph、GraphImpl和GraphOps这三个类,我们在前面图的操作部分已经基本分析了它们内部的主要操作方法,下面我们主要结合源码分析一下Spark GraphX的VertexRDD、EdgeRDD和EdgeTriplet三种数据类型和点分割的四种PartitionStrategy(分割存储策略)。
1.VertexRDD
VertexRDD[VD]继承自RDD[(VertexID,VD)],并增加了一些额外的限制,VertexID表示的是顶点的ID每个并且VertexID只出现一次。此外,VertexRDD[VD]表示一个顶点集合,其中每个顶点的属性是VD。本质上VertexRDD[VD]一个可重复使用的HashMap(哈希表)。利用VertexID这个索引可以快速查找到需要的顶点,对于VertexRDD[VD],它提供了以下常用的操作方法。
(1)filter()方法:filter()方法用来过滤满足pred函数的顶点集合。filter()方法保留了原始VertexRDD的索引结构,本质上是对每个VertexRDD的Partition进行计算,返回的是一个VertexRDD。代码如下:

(2)mapValues()方法:mapValues()方法是通过函数f对顶点的属性(VD)进行操作最终返回的是一个顶点属性是VD2的VertexRDD。代码如下:
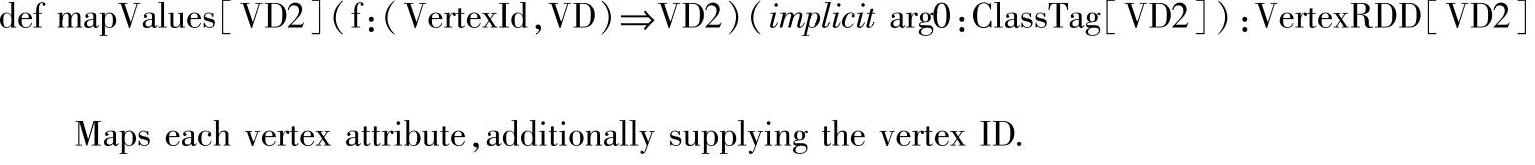
(3)diff()方法:diff()方法用来比较两个VertexRDD的不同,返回的是调用diff()的VertextRDD中存在而other VertexRDD中不存在的元素构成的新的VertexRDD。需要注意的是两个VertexRDD中的顶点ID集(VertexIdToIndexMap)必须相同。代码如下:
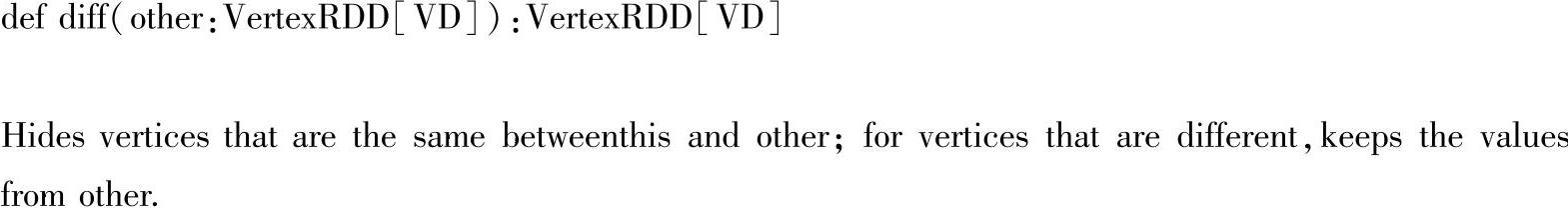
(4)innerJoin()方法:用来对具有相同VertexId的VertexRDD进行连接,并通过函数f生成新的顶点属性,返回一个由在两个VertexRDD中都存在的顶点构成的VertexRDD。代码如下:

(5)aggregateUsingIndex()方法:aggregateUsingIndex()方法用来对具有相同VertexID(顶点ID)的两个VertextRDD通过函数reduceFunc进行操作。代码如下:

其中参数messages指的是由目的顶点ID和它接受到的消息数据作为属性构成的Ver-texRDD,函数reduceFunc会对messages中VertexId相同的属性值(VD2)进行聚合操作,聚合后的VD2属性值会作为调用aggregateUsingIndex()方法的VertexRDD的顶点的属性值,最终返回的是一个由VertexID和聚合后的顶点属性值构成的VertexRDD,需要注意的是,不包含messages中的VertexId的顶点将会被舍弃。
2.EdgeRDD
EdgeRDD[ED,VD]继承自RDD[Edge[ED],EdgeRDD内的边是以点分割的方式分成不同的块来进行管理的,具体的分区策略通过PartitionStrategy指定。在每个分块中,边属性和邻接顶点信息分别存储,这使得更改边属性值时能够最大限度的复用邻接顶点的信息。EdgeRDD还提供的三个额外的函数。
(1)mapValues()方法:mapValues()方法是应用函数f于EdgeRDD的边属性,只改变EdgeRDD的边属性的值,而不改变EdgeRDD划分时的结构。代码如下:

(2)innerJoin()方法:innerJoin()方法是对两个EdgeRDD进行连接操作,这里的两个EdgeRDD必须是相同的PartitionStrategy(分割策略),最后返回一个新的EdgeRDD。代码如下:

其中新EdgeRDD的边属性的值是通过函数f得到的,并且新EdgeRDD保留的是只有在原先两个EdgeRDD都出现过的边。
(3)reverse()方法:reverse()方法是对EdgeRDD中所有的边进行反转操作,也就是说改变EdgeRDD中源顶点和目的顶点连接的边的方向。代码如下:
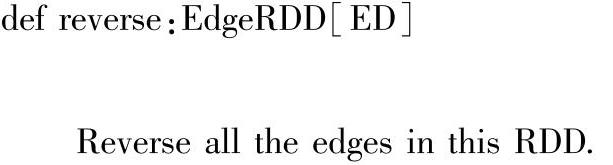
3.EdgeTriplet
EdgeTriplet[VD,ED]是Spark GraphX特有的一种数据类型,它是顶点和边的结合,它继承自Edge[ED],并同时在类内部加入源顶点的属性(srcAtrr)和目的顶点属性(dstAttr)信息作为自己的属性,由于它的父类Edge[ED]本身包含源顶点ID、目的顶点ID和边属性,所以一个Edgetriplet[VD,ED具有源顶点的ID和属性、目的顶点ID和属性以及边属性,本质上来讲EdgeTtriplet是对Edge[VD]的一层封装。EdgeTriplet[VD,ED]这种数据类型的优势就是在图的数据遍历方面提供了方便。我们可以看下以下伪代码中EdgeTriplet[VD,ED]的使用,下面的伪代码是通过图的triplets操作生成一个RDD[EdgeTriplet[VD,ED]]对象,然后调用RDD的collect()方法生成一个单机的Scala数组,该数组中的元素是有一组Edge-Triplet[VD,ED]对象组成的,这样就可以通过EdgeTriplet[VD,ED]遍历边的源顶点属性和目的顶点属性。

4.PartitionStrategy
前面的小节我们已经简单介绍过Spark GraphX是采用点分割的模式对图的数据进行分布式存储的,在使用点分割的时候可以使用不同的PartitionStrategy(划分策略)对图数据进行划分,不同的PartitionStrategy会影响到缓存的Ghost副本数量以及每个EdgePartiton分配的边的均衡程度等,所以我们在使用PartitionStrategy时要结合图的结构特征选取最佳策略。
PartitionStrategy本身是一个trait(特质),我们在使用它的时候,可以继承它然后实现它内部的getPartition()方法来实现自定义的划分策略,当然也可以使用Spark GraphX本身内置的划分策略,目前内置的有EdgePartition1D、EdgePartition2D、RandomVeertexCut和Canon-icalRandomVertexCut这4种划分策略。下面我们结合它们的源码实现一一介绍每种划分策略的特点。
(1)EdgePartition1D:EdgePartition1D是根据边的源顶点ID和PartitionID进行对图数据进行划分的,这种策略可以将所有源顶点相同的边放到一个分区里。PartitionID是图的分区大小的整数标识,默认必须小于2^30。mixingPrime是一个固定的Long Int值,它主要用来划分时平衡图数据使得数据均匀地分布在集群的结点上,同时可以增强数据分布的随机性。,当然mixingPrime无法从根本上解决数据分布的不均匀,只是减少这种情况发生的概率。
 (https://www.xing528.com)
(https://www.xing528.com)
(2)EdgePartition2D:EdgePartition2D采用的是二维的邻接矩阵的划分方式将边划分到numParts个分区中,这种划分方式可以保证顶点的复制个数的上限是2*sqrt(numParts)个,它同时会尽可能地平衡边在结点上的分布。EdgePartition2D的划分步骤如下:首先,getPar-tition()中的val ceilSqrtNumParts:PartitionID=math.ceil(math.sqrt(numParts)).toInt这行代码用来获取分配矩阵的平方根因子;然后,EdgePartition2D同样引入了一个固定的Long Int值mixingPrime,使用mixingPrime和ceilSqrtNumParts进行计算增加源顶点ID和目的顶点ID划分的随机性和均匀性;最后通过(col*ceilSqrtNumParts+row)%numParts这行代码把边均匀地划分到numParts个分区。
下面是EdgePartition2D的一个划分案例,即基于11个顶点的图,并划分到9个分区,具体划分示意图及其划分细节如下。


(3)RandomVeertexCut:RandomVeertexCut是随机顶点划分的,首先根据源顶点ID和目的顶点ID进行哈希值计算,对求得的哈希值取绝对值,然后除以numParts求得划分个数。需要注意的是这样的划分方式会将两个顶点之间方向相同的边划分到同一个分区中去。

(4)CanonicalRandomVertexCut:CanonicalRandomVertexCut的划分策略和RandomVertex-Cut相似,不同的是在对源顶点ID和目的顶点ID进行哈希值计算前会先根据顶点的ID进行排序,使得源顶点ID和目的顶点ID中值小的那个排在前面,然后再对求得的哈希值取绝对值并除以numParts求得划分个数。这样做的好处就是可以将两个顶点之间的所有边放在同一个分区中,完全不用考虑边的方向是否相同。

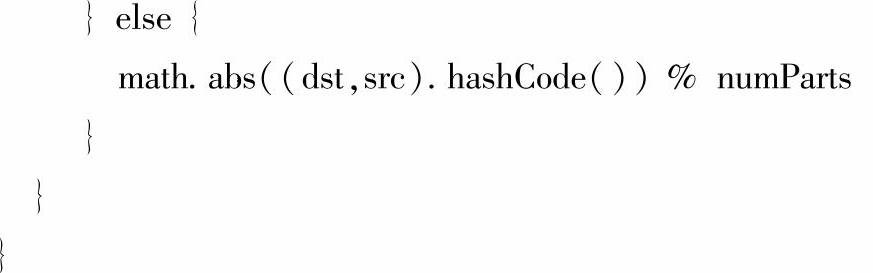
8.3.3 Spark GraphX图算法的实现方法
基于Prege模型,Spark GraphX提供了一系列图算法来简化任务的分析。这些算法包含在org.apache.spark.graphx.lib包中(如图8-9所示),在GraphOps类中封装了对这些图算法进行直接调用的方法,同时由于Spark采用了Scala语言的隐式转换方法,所以Graph可以直接调用GraphOps类中的这些方法完成对图数据的特殊处理。我们结合图8-4来分析一下常用的图算法。

图8-9 Spark GraphX中图算法源码的目录结构
1.PageRank
PageRank,又称网页排名,网页级别。它是Google专有的算法,用于衡量特定网页相对于搜索引擎索引中的其他网页而言的重要程度。它由Google公司的创始人Larry Page和Sergey Brin在20世纪90年代后期发明的。PageRank实现了将链接价值概念作为排名因素。
PageRank把页面的链接看成是一个投票,来指示该页面的重要性。具体地来说,Pag-eRank通过互联网浩瀚的超链接关系来确定一个页面的等级,一个页面的超链接相当于对该页投一票,一个页面的PageRank值是由所有链向它的页面(链入页面)的重要性经过递归算法得到的。一个有较多链入的页面会有较高的等级,相反如果一个页面没有任何链入页面,那么它就没有等级。例如在Google搜索中,Google搜索引擎会把从A页面到B页面的链接解释为A页面给B页面投票,Google根据投票来源(甚至来源的来源,即链接到A页面的页面)和投票目标的等级来决定新的等级。简单的说,一个高等级的页面可以使其他低等级页面的等级提升。
下面我们通过源代码看一下PageRank算法在Spark GraphX中的实现。
(1)在GraphOps类中提供了pageRank()方法,在pageRank()方法继续调用PageRank的runUntilConvergence()方法。这样设计的好处是即使我们不了解PageRank算法的具体实现,也可以很容易的去使用它进行图数据的计算。

(2)继续跟踪PageRank的runUntilConvergence()方法,在runUntilConvergence()方法的参数中,参数graph指的要使用PageRank处理的图;参数tol是一个收敛值,传入的这个值越小PageRank计算的值就越精确,但是如果要计算的图数据量很大而设置的tol值很小就会产生巨大的计算任务并消耗更多的时间,所以要结合自己CPU和内存的实际情况来设置这个值;参数resetProb是一个随机重置的默认值。


通过以上代码可以看到,在runUntilConvergence()方法最重要的还是vertexProgram,、sendMessage,、messageCombiner这三个函数的实现,它们会作为Pregel的参数传给Pregel模型进行图数据的计算。
2.SVDPlusPlus
SVDPlusPlus,就是指SVD++算法,它是在SVD算法的基础上通过利用更多的信息衍生出来的算法。SVD(singular valur decomposition,奇异值分解法),是线性代数中一种重要的矩阵分解,是矩阵分析中正规矩阵酉对角化的推广。在信号处理、统计学等领域有重要应用。在图计算中,我们主要用在进行社交网络和推荐系统上。
例如要预测用户A对一部电影M的评分,而手上只有用户A对若干部电影的评分和用户B对若干部电影的评分(包含M的评分),就可以使用SVDPlusPlus算法来进行操作。它会根据已有的评分情况,分析出评分者对各个因子的喜好程度以及电影包含各个因子的程度,最后再反过来根据分析结果预测评分。电影中的因子可以理解成这些东西:电影的搞笑程度,电影的爱情爱得死去活来的程度,电影的恐怖程度等等,SVDPlusPlus的想法抽象来看就是将一个N行M列的评分矩阵R(R[u][i]代表第u个用户对第i个物品的评分),分解成一个N行F列的用户因子矩阵P(P[u][k]表示用户u对因子k的喜好程度)和一个M行F列的物品因子矩阵Q(Q[i][k]表示第i个物品的因子k的程度)。用公式来表示就是:R=P*T(Q),R的元素数值越大,表示用户越喜欢这部电影。P的元素数值越大,表示用户越喜欢对应的因子。Q的元素数值越大,表示物品对应的因子程度越高。分解完后,就能利用P,Q来预测用户A对某电影的评分了。
3.TriangleCount
TriangleCount,是指三角形计数算法,当一个顶点有两个相邻的顶点以及相邻顶点之间的边时,这个顶点是一个三角形的一部分。Spark GraphX在TriangleCount object中实现了一个三角形计数算法,它计算通过每个顶点的三角形的数量。需要注意的是,在计算社交网络数据集的三角形计数时,TriangleCount需要边的方向是规范的方向(srcId<dstId),并且图通过Graph类的partitionBy()方法进行过分区。
4.ConncetedComponents
ConncetedComponents,指的是连通分支图算法,连通分支图算法用ID标注图中每个连通分支,将连通分支中序号最小的顶点的ID作为连通分支的ID。该算法是图深度优先搜索算法的另一重要应用,它可以将一个大图分解成多个连通分支,然后分别在各个联通分支上独立运行计算,最后再根据分支之间的关系将所有的解组合起来。例如,在社交网络中,连通分支可以近似为集群,Spark GraphX在ConnectedComponents object中包含了连通分支算法的实现,我们可以通过ConnectedComponents object中run()方法内的实现来计算社交网络数据集中的连通分支图。
5.StronglyConnected Components
StronglyConnected Components,指的是强连通分支算法,它的实现和Connected Compo-nents算法很类似,不同在于它处理的对象是一个强连通分支图。对于强连通分支,我们可以可以理解为:在有向图中,如果任意两个点能够互相联系,那么这就称为强连通分支,对于给定一个有向图,它不一定是强连通的,但一定可以分为多个强连通分支。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




