Pregel图计算框架：高效的分布式计算

1.Pregel简介

Pregel是Google公司于2010年推出的一个用于分布式图计算的计算框架，主要用于图遍历（BFS）、最短路径（ShortestPaths）、PageRank等图算法的使用。Pregel借鉴MapReduce的思想，提出了“像顶点一样思考（Think Like A Vertex）”的图计算模式，用户使用它时不需要考虑并行分布式计算的细节，只需要实现一个顶点更新函数，然后在该顶点上不断地进行算法迭代和数据同步。Pregel采用的是基于顶点的边分割，然后将图数据分成若干个分区存储到各个结点的模式，其中每个分区包含的是一组顶点和以这组顶点为源顶点的边，结点之间通过发送消息来完成操作，图数据的同步机制采用的是BSP模型（整体同步并行计算模型）。

2.BSP模型

对于BSP模型在数据同步方面的处理思想，我们可以结合图8-7做如下解释。

（1）Processors指的是并行计算进程，它对应到集群中的多个结点，每个结点可以有多个Processor；

（2）LocalComputation就是单个Processor的计算，每个Processor都会切分一些结点作计算；

（3）Communication指的是Processor之间的通讯。图计算往往需要做些递归或是使用全局变量，在BSP模型中，对图结点的访问分布到了不同的Processor中，并且往往哪怕是关系紧密具有局部聚类特点的结点也未必会分布到同个Processor或同一个集群结点上，所有需要用到的数据都需要通过Processor之间的消息传递来实现同步；

（4）BarrierSynchronization又叫障碍同步或栅栏同步。每一次同步也是一个超步的完成和下一个超步的开始；

（5）Superstep（超步），这是BSP的一次计算迭代，拿图的广度优先遍历来举例，从起始结点每往前步进一层对应一个超步；

（6）程序该什么时候结束是由程序自己控制，一个作业可以选出一个Proceessor作为Master，每个Processor每完成一个Superstep都向Master反馈完成情况，Master在N个Super-step之后发现所有Processor都没有计算可做了，便通知所有Processor结束并退出任务。

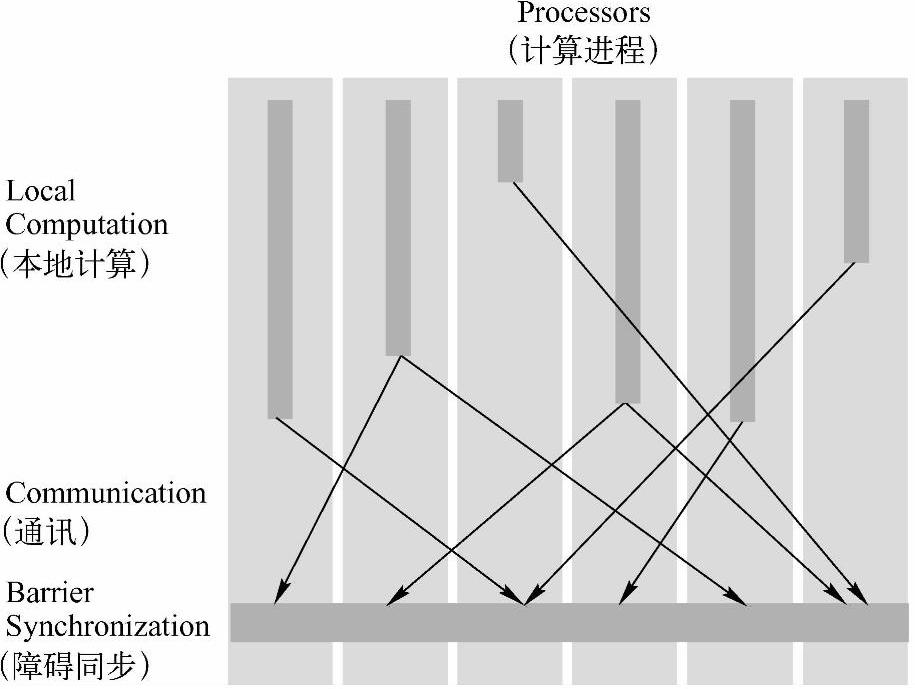
图8-7 BSP模型图

3.Pregel计算过程

在了解了BSP模型的处理思想后，我们继续分析Pregel的计算过程。在Pregel的计算模型中，输入的数据是一个有向图，该有向图的每一个顶点都有一个相应的vertex identifier（顶点ID）和顶点属性，这些顶点属性可以被修改，其初始值由用户定义。每一条有向边都和其源顶点关联，并且也拥有一些用户定义的属性值，并同时还记录了其目的顶点的ID。

一个典型的Pregel计算过程如下。

（1）读取输入，初始化该图；(www.xing528.com)

（2）当图被初始化好后，运行一系列的Supersteps（超步），每一次Superstep都在全局的角度上独立运行，直到整个计算结束，输出结果。

在每一次的Superstep中，顶点的计算都是并行的，每一次执行用户定义的同一个函数。每个顶点可以修改其自身的状态信息或以它为起点的出边的信息，从前序Superstep中接受消息，并传送给其后续Superstep，或者修改整个图的拓扑结构。边在这种计算模式中并不是核心对象，没有相应的计算运行在其上。

算法是否能够结束取决于是否所有的顶点都已经通过“Vote”（搜索）标识其自身达到“halt”状态（投票停止状态）了。在Superstep 0，所有顶点都会被置于Active（活跃）状态，每一个Active的顶点都会在计算执行的某一次的Superstep中被计算。顶点通过将其自身的状态设置成“halt”来表示它已经不再Active。这就表示该顶点没有进一步的计算需要进行，而Pregel框架将不会在接下来的Superstep中计算该顶点，除非该顶点收到一个其他Superstep传送的消息。如果顶点接收到Message（消息），该Message将该顶点重新置Ac-tive，那么在随后的计算中该顶点必须在此通过投票停止设置自己的状态为停止状态。整个计算在所有顶点都达到“Inactive”（活动中）状态，并且没有Message（消息）在传送的时候宣告结束。这种简单的状态机制可以参考图8-8中的描述。

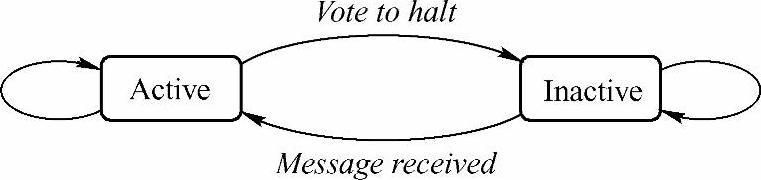
图8-8 Vertex状态机

整个Pregel程序的输出是所有顶点输出的集合。通常来说Pregel程序的输出是跟输入是同构的有向图，但是并非一定是这样，因为在计算的过程中，可以对顶点和边进行添加和删除。比如一个聚类算法，就有可能从一个大图中选出满足需求的几个不相连的点；一个对图的挖掘算法就可能仅仅是输出了从图中挖掘出来的聚合数据等。

4.Pregel在Spark GraphX中的实现

在Spark GraphX的GraphOps类中提供了一个pregel（）方法来实现Pregel模型，需要注意的是Spark GraphX中的Pregel模型并不严格遵循标准的Pregel模型，它是一个参考了GAS模型（邻居更新模型）后改进的模型。下面我们可以结合GraphOps类源码中的pregel（）方法来分析一下在Spark GraphX中Pregel模型的实现。pregel（）方法的代码如下：

pregel（）是一个柯里化方法，在第二个参数列表中的参数是三个函数vprog、sendMsg和mergeMsg，而标准的Pregel模型在这种情况下接受的是一个messageList（消息列表），这也是基于MapReduceTriplets（）方法的Pregel模型和标准的Pregel的最大区别，它不会在单个顶点上进行消息的遍历，而是将多个Ghost（虚点）副本收到的消息聚合后，发送给Master（主点）副本，在使用vprog函数来更新顶点的属性值，消息的接受和发送都被自动并行化处理，不用担心超级结点（指出入度大的结点）的问题。

在pregel（）方法中会通过Pregel（graph，initialMsg，maxIterations，activeDirection）（vprog，sendMsg，mergeMsg）这行代码调用Pregel类的apply（）方法继续完成实现。其中参数graph指的是向Pregel模型中传入的图数据；参数initialMsg指的是初始化状态下向Pregel模型发送的消息；参数maxIterations指的是Pregel模型最大的迭代次数，当执行Pregel模型达到max-Iterations设置的次数后如果程序仍然没有收敛则会强制停止执行；参数activeDirection指的是sendMsg函数在计算时的收集方向，sendMsg函数会根据源顶点、目的顶点和收集方向来判断EdgeTriplet[VD，ED]是否处于活跃状态来进行计算。在第2段参数中，vprog、sendMsg和mergeMsg都是用户自定义函数，其中vprog函数在每个顶点上执行，对输入的数据进行计算后生成新的顶点属性值；sendMsg函数在每个活跃的EdgeTriplet[VD，ED]上运行，生成发送给下一次迭代的消息；mergeMsg函数用于将发送给顶点的两条消息进行合并为一条消息。

下面我们看一下Pregel的apply（）方法的源码实现：

通过以上源码可以看到，Spark GraphX的Pregel实现综合了标准Pregel和GAS模型两者的优点，接口相对简单，又能保证性能，可以应对点分割的图存储模式，胜任符合幂律分布的自然图的大型计算。