图是由若干给定的顶点及连接两点的边所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系,用顶点代表事物,用连接两点的边表示相应两个事物之间的关系。图是图论的基本研究对象。
图可以分为有向图、无向图和单图。如果给图的每条边规定一个方向,那么得到的图称为有向图。在有向图中,与一个结点相关联的边有出边和入边之分。相反,边没有方向的图称为无向图。一个图如果任意两顶点之间只有一条边(在有向图中为两顶点之间每个方向只有一条边),边集中不含环,则称为单图。
如图8-1所示,分别对应了有向图、无向图以及一个无向的单图的简单示例。
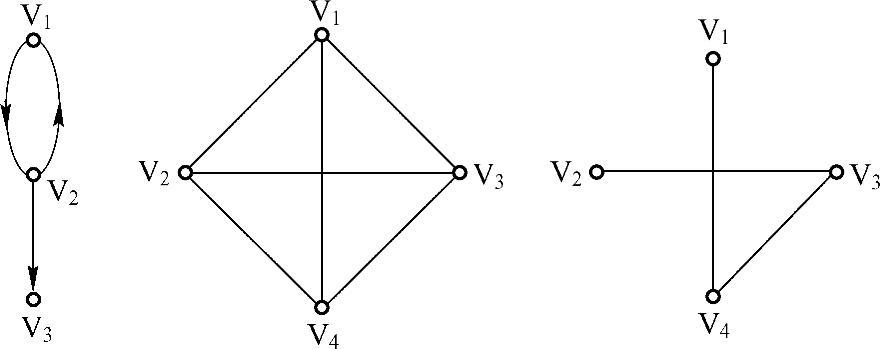
图8-1 有向图、无向图以及单图的示例
图的存储结构除了要存储图中各个顶点的本身信息外,同时还要存储顶点与顶点之间的所有关系(边的信息),因此,图的结构比较复杂,很难以数据元素在存储区中的物理位置来表示元素之间的关系,但也正是由于其任意的特性,故物理表示方法很多。常用的图的存储结构有邻接矩阵、邻接表、十字链表和邻接多重表。
下面看一下关于图的一些基本术语。
●阶(Order):图G中顶点(vertex)集V的大小称作图G的阶。
●子图(Sub-Graph):当图G′=(V′,E′),其中V′包含于V,E′包含于E,则G′称作图G=(V,E)的子图。每个图都是本身的子图。
●生成子图(Spanning Sub-Graph):指满足条件V(G′)=V(G)的G的子图G。(https://www.xing528.com)
●导出子图(Induced Subgraph):以图G的顶点集V的非空子集V1为顶点集,以两端点均在V1中的全体边为边集的G的子图,称为V1导出的导出子图;以图G的边集E的非空子集E1为边集,以E1中边关联的顶点的全体为顶点集的G的子图,称为E1导出的导出子图。
●度(Degree):一个顶点的度是指与该顶点相关联的边的条数,顶点v的度记作d(v)。
●入度(In-degree)和出度(Out-degree):对于有向图来说,一个顶点的度可细分为入度和出度。一个顶点的入度是指与其关联的各边之中,以其为终点的边数;出度则是相对的概念,指以该顶点为起点的边数。
●自环(Loop):若一条边的两个顶点为同一顶点,则此边称作自环。
●路径(Path):从u到v的一条路径是指一个序列v0,e1,v1,e2,v2,…,ek,vk,其中ei的顶点为vi及vi-1,k称作路径的长度。如果它的起止顶点相同,该路径是“闭”的,反之,则称为“开”的。一条路径称为一简单路径(Simple Path),如果路径中除起始与终止顶点可以重合外,所有顶点两两不等。
●行迹(Trace):如果路径P(u,v)中的边各不相同,则该路径称为u到v的一条行迹。
●轨道(Track):如果路径P(u,v)中的顶点各不相同,则该路径称为u到v的一条轨道。
●闭的行迹称作回路(Circuit),闭的轨道称作圈(Cycle)。现存文件中的命名并无统一标准,比如另一种定义是:walk对应上述的path,path对应上述的track。Trail对应trace。
●桥(Bridge):若去掉一条边,便会使得整个图不连通,该边称为桥。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




