逻辑函数卡诺图化简方法

一、最小项合并的规律

由于卡诺图中的最小项是按几何相邻与逻辑相邻重合的规律排列的，因此，凡是几何相邻的最小项均可以合并。利用卡诺图合并最小项有2种方法：采用圈1的方法，得到原函数；采用圈0的方法，得到反函数。通常我们采用圈1的方法。

最小项合并时可消去相关变量，但必须满足2n个最小项才能合并，即2个最小项合并可消去1个变量，4个最小项合并可消去2个变量，8个最小项合并可消去3个变量，依此类推，2n个最小项合并可消去n个变量。

最小项合并的方法：消去互反的变量，保留共有的变量。

图2.6.8、图2.6.9、图2.6.10中分别给出了两个相邻最小项、四个相邻最小项、八个相邻最小项合并的规律。

图2.6.8　两个相邻最小项的合并

（a）Y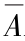＝B；（b）Y＝A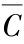；（c）Y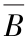＝C

图2.6.9　四个相邻最小项的合并

（a）Y＝C；（b）Y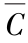＝；（c）Y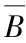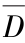＝；（d）Y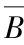＝D

图2.6.10　八个相邻最小项的合并

（a）Y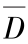＝；（b）Y＝B

二、用卡诺图化简逻辑函数

利用卡诺图化简逻辑函数的方法称为图形法。它和公式法相比具有两个优点：一是不用熟记公式和定理；二是公式法化简时，是否为最简式很难判断，而卡诺图化简利用几何相邻和逻辑相邻性，很容易得到最简式。

1.卡诺图化简的步骤

（1）画出逻辑函数对应的卡诺图。

（2）合并相邻的最小项，即圈组。

（3）写出最简与或式：每个圈合并后用一个与项表示，然后将每个与项相或即得到最简与或式。

2.合并最小项（圈组）时应注意的几点

（1）必须是2n个几何相邻的最小项进行合并，消去n个变量，得到共有的因子。

（2）合并最小项时，圈尽可能地大，圈的个数尽可能地少。因为圈越大，消去的变量就越多；圈的个数越少，对应的与项就越少，函数表达式才越简单。

（3）每个最小项至少圈一次，可以重复被圈。但每个圈中至少包含1个新的最小项（只被圈过一次），否则该圈是多余的。(www.xing528.com)

（4）注意卡诺图的循环相邻性。即相邻方格包括上下底相邻、左右边相邻和四个角相邻。

（5）有时合并最小项的方法并不是唯一的，故得到的最简式也不是唯一的。

[例2.6.7]　用卡诺图化简逻辑函数Y（A，B，C，D）＝∑m（0，4，5，11，12， 13， 15）。

解：（1）画出函数对应的卡诺图，如图2.6.11所示。

（2）包圈合并最小项，得最简与或式。

[例2.6.8]　用卡诺图化简逻辑函数。

解：（1）画出函数对应的卡诺图，如图2.6.12所示。

图2.6.11　[例2.6.7]的卡诺图

图2.6.12　[例2.6.8]的卡诺图

（2）包圈合并最小项，得最简与或式。

[例2.6.9]　用卡诺图化简逻辑函数Y（A，B，C，D）＝∑m（0，1，2，3，4， 5， 6， 8， 9， 10， 11， 12， 13， 14）。

解：（1）画出函数对应的卡诺图，如图2.6.13所示。

图2.6.13　[例2.6.9]的卡诺图

（a）圈1的卡诺图；（b）圈0的卡诺图

（2）包圈合并最小项，得最简与或式。

方法一：用圈1的方法化简，如图2.6.13（a）所示，得

方法二：用圈0的方法化简，如图2.6.13（b）所示，得

再对函数Y求反，得

两种方法结果相同。