逻辑函数的卡诺图表示法优化：

一、卡诺图的画法

卡诺图也叫真值图，是逻辑函数真值表的几何图形表示法。它是将逻辑函数的最小项按一定的规律排列而成的方格矩阵，每个小方格对应一个最小项，因此，卡诺图又叫最小项方格图。

画卡诺图的具体步骤如下：

（1）n个输入变量的逻辑函数画出2n个小方格，每个小方格对应一个最小项。

（2）各变量的取值符合几何相邻和逻辑相邻重合的原则，即变量的取值按循环码（也叫格雷码）的顺序排列。

这里先介绍几何相邻和逻辑相邻的定义。

几何相邻：卡诺图中在几何位置上下左右相接的最小项。每一行或每一列两端的最小项也具有几何相邻性，故卡诺图可看成一个上下、左右对折的立体图形的展开形式。

逻辑相邻：只有一个变量互为反变量，其余变量均相同的两个最小项叫作在逻辑上是相邻的。如三变量ABC和中只有C和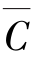不同，其余变量相同，所以ABC和是逻辑相邻的最小项。

两个逻辑相邻项可以进行合并，，因此，两个逻辑相邻项可合并为一项，合并的结果为两个最小项的共有因子，消去互补因子。

下面分别介绍二变量到四变量卡诺图的画法。

二变量的卡诺图：二变量A、B共有22＝4个最小项，、m3＝AB，根据其相邻性可画出图2.6.1所示的卡诺图。由图可以看出：横向变量和纵向变量相交的小方格表示的最小项为这些变量的与组合，如果其中原变量用1表示，反变量用0表示，则卡诺图可用最小项编号表示。

图2.6.1　二变量的卡诺图

（a）方格内标最小项；（b）方格内标最小项编号；（c）简化形式

三变量的卡诺图：三变量A、B、C共有23＝8个最小项，为了符合几何相邻和逻辑相邻重合的原则，变量BC的取值不是按自然二进制数的顺序（00、01、10、11）排列，而是按格雷码的顺序（00、01、11、10）排列的。三变量的卡诺图还可以画成如图2.6.2（d）的形式。

图2.6.2　三变量的卡诺图

（a）方格内标最小项；（b）方格内标最小项编号；（c）简化形式；（d）其他形式的画法

四变量的卡诺图：四变量A、B、C、D共有24＝16个最小项，为了符合几何相邻和逻辑相邻重合的原则，横向变量AB和纵向变量CD均按格雷码的顺序排列，如图2.6.3所示。

图2.6.3　四变量的卡诺图

（a）方格内标最小项；（b）简化形式

二、逻辑函数的卡诺图表示法

采用卡诺图化简逻辑函数时，必须先画出逻辑函数对应的卡诺图。常用的方法有2种，由真值表画逻辑函数卡诺图或由表达式画逻辑函数卡诺图。

1.由真值表画逻辑函数卡诺图(www.xing528.com)

方法：将真值表中每组输入变量的取值组合所对应的函数值填入卡诺图相应的小方格中，即函数值为1的最小项所对应的小方格中填1，函数值为0的最小项所对应的小方格中填0。

[例2.6.3]　画出表2.6.2对应的卡诺图。

表2.6.2　[例2.6.3]的真值表

解：表中所描述的是三变量的逻辑函数。

（1）画出三变量的卡诺图。

（2）填写卡诺图。由于表中对应变量取值组合001、011、101、111的函数值为1，故在卡诺图中相应的小方格内填1，其余的小方格填0。如图2.6.4所示。

2.由表达式画逻辑函数卡诺图

（1）由标准与或式画逻辑函数卡诺图。

方法：先根据输入变量个数画出卡诺图，然后在卡诺图中将标准与或式中的每个最小项对应的小方格填入1，其余的小方格填0。

图2.6.4　[例2.6.3]卡诺图

图2.6.5　[例2.6.4]卡诺图

（2）由一般与或式画逻辑函数卡诺图。

方法：首先画出输入变量对应的卡诺图；然后根据表达式中与项的特征将最小项填入卡诺图，具体如下：与项中的原变量用1表示，非变量用0表示，与项中的变量在卡诺图中横向和纵向相交的小方格便为所求的最小项，填入1，其余的小方格填0。

当然，也可以先将一般与或式变换为最小项表达式，然后将最小项填入对应的卡诺图。但这种方法十分烦琐，而且容易出现差错，一般不建议采用。

（3）由非与或式画逻辑函数卡诺图

方法：将非与或式变成一般与或式，再由一般与或式画逻辑函数卡诺图。

[例2.6.6]　画出逻辑函数对应的卡诺图。

解：先将函数变为一般与或式，得

然后用上述方法画出与或式对应的卡诺图，如图2.6.7所示。

图2.6.6　[例2.6.5]卡诺图

图2.6.7　[例2.6.6]卡诺图