一、代入规则
在任何一个逻辑等式中，如果将等式两边所有的同一变量均用同一个逻辑函数式代入，等式依然成立，这就是代入规则。
利用代入规则很容易将摩根定律的基本公式推广为多变量的形式。
[例2.4.2] 用代入规则证明摩根定律也适用于多变量的情况。
解：已知二变量的摩根定律为
现以C＋D同时代入等式左边和右边B的位置，得
依此类推，摩根定律对任意多个变量都成立。
二、反演规则
对于任何一个函数表达式Y，若将其中所有的“·”换成“＋”，“＋”换成“·”，“0”换成“1”，“1” 换成“0”，原变量换成反变量，反变量换成原变量，则得到的结果就是原函数Y的反函数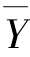
，这个规则称为反演规则。
反演规则为求已知逻辑表达式的反逻辑表达式提供了方便。
在使用反演规则时，还须注意以下两点：
（1）保持原来运算的优先顺序，即先进行括号内的运算，再进行与运算，后进行或运算。(www.xing528.com)
（2）不属于单个变量上的非号保持不变。
回顾一下摩根定律便可发现，它只不过是反演规则的一个特例而已。正是由于这个原因，才将它称为反演律。
[例2.4.3] 已知
，求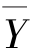
。
解：根据反演规则可写出
如果利用基本公式和常用公式进行求反运算，也可得到同样结果，但是常常要麻烦得多。
三、对偶规则
对于任何一个逻辑函数式Y，若将其中所有的“·”换成“＋”，“＋”换成“·”，“0” 换成“1”，“1” 换成“0”， 则得到一个新的逻辑式 Y′。 Y′为 Y的对偶式，这就是对偶规则。
[例2.4.4] 已知
， 求 Y′。
解：根据对偶规则可写出
与反演规则相同，在使用对偶规则写出逻辑函数的对偶式时，同样应注意保持原来运算的优先顺序，同时，所有变量上的非号都保持不变。
如果两个逻辑表达式相等，则它们的对偶式也必定相等。故有时证明两个逻辑表达式相等可以通过证明它们的对偶式相等来完成，因为有些情况下证明它们的对偶式相等更加容易。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
