Streeter-Phelps（S-P）模型及其优化

1.S—P模型基本方程及其解

斯特里特(H.Streeter)和菲尔普斯 (E.Phelps)于1925年提出了河流水质的第一个模型，即S-P模型，它是描述一维河流中BOD和DO消长变化规律的模型，S—P模型得到广泛的应用。

S-P模型的建立基于两项假设：

(1)只考虑好氧微生物参加的BOD衰减反应，并认为该反应为一级反应，符合一级反应动力学。

(2)认为耗氧的原因只是BOD衰减反应引起的。BOD的衰减反应速率与河水中溶解氧(DO)的减少速率相同，复氧速率与河水中的亏氧量D成正比。

S—P模型的基本方程为：

式中 L——河水中的BOD值，mg/L；

D——河水中的亏氧值，即饱和溶解氧浓度OS(mg/L)与河水中的实际溶解氧浓度O (mg/L)的差值，mg/L；

k1——河水中BOD衰减(耗氧)速度常数，d-1；

k2——河水中的复氧速度常数，d-1；

t——河水中的流行时间，d。

图7-13　BOD—DO的S—P模型

式中 u——河段平均流速，m/s。

在水质参数值和初始条件确定后，根据S—P模型的解即可获得BOD—DO随x的变化情况，如图7-13所示。

2.S-P模型的临界点和临界点氧浓度

从图7-13可见，在河流的某一距离x处，溶解氧具有最小值。此处水质最差，是人们较为关注的。此处的亏氧值 (或溶解氧值)及发生的距离，可通过求极值的方法求得，即可由式[7-74 (b)]，令d O/d x=0，得到：

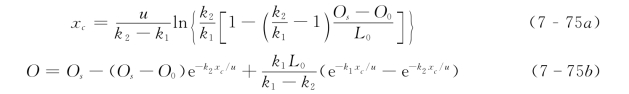
S—P模型广泛地应用于河流水质的模拟预测中，是预测河流中BOD和DO变化规律的较好模型。它也应用于计算河流的最大允许排污量。(www.xing528.com)

3.S—P模型的缺陷和修正方法

在式[7-75 (b)]中，若初始浓度L0相当大，则计算出的临界溶解氧浓度将出现负值，这是不符合实际情况的，说明S—P模型对BOD污染严重的水质计算是不能令人满意的。为了弥补S—P模型的这个缺陷，Shastry等人提出了非线性模型：

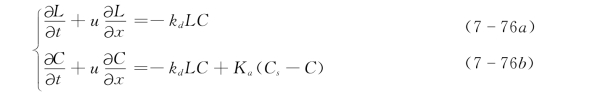
该模型虽然不会出现负值解，但求解难度较大，对结果的分析也不够直观。

4.S—P模型的修正型

S—P模型的两项假设是不完全符合实际的。河水中所含的悬浮物微粒、有机物在河水流速较低时可沉降到河底，而原来沉降的底泥在河水流速较高时又可重新转变为悬浮态。沉淀过程中使得河水中的部分需氧有机物脱离了河水的耗氧过程，使得河水中的BOD减低，再悬浮使得底泥中的需氧有机物进入河水，加入河水的耗氧过程，致使河水的BOD值增高。这一沉淀、再悬浮过程影响了河水中的溶解氧平衡，从而使得S—P模型计算不准确，为了计算河流水质的这些特殊问题，人们在S-P模型的基础上附加一些新的假设，推导出了一些新的模型。

(1)托马斯(Thomas)模型。托马斯在S—P模型的基础上，增加一项因悬浮物的沉淀与上浮所引起的BOD速率变化。其方程为：

式中 k3——沉浮系数，d-1。

沉浮系数k3既可以大于零，也可以小于零，对于冲刷、再悬浮过程，k3＜0，对于沉淀过程，k3＞0。

(2)多宾斯—坎普(Dobbins—Camp)模型。对一维稳态河流，在托马斯模型的基础上，多宾斯—坎普提出了两条新的假设：

1)考虑地表径流和底泥耗氧所引起的BOD变化速率，该速率以R表示。

2)考虑藻类光合作用和呼吸作用以及地面径流所引起的溶解氧变化速率，该速率以P表示。

多宾斯—坎普采用以下基本方程组：

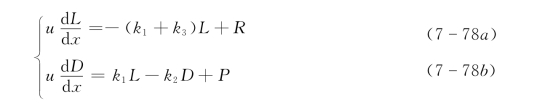
(3)奥康纳(O′Connon)模型。对一维稳态河流，在托马斯模型的基础上，奥康纳提出的假设条件为：总BOD是碳化和硝化BOD两部分之和，即L=Lc+Ln。则托马斯修正式可改写为：

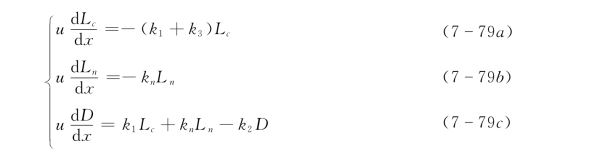
式中 kn——硝化BOD衰减速度常数，d-1；

Lc0——河流x=0处，含碳有机物BOD浓度，mg/L；

Ln0——河流x=0处，含氮有机物BOD浓度，mg/L。